Una guida all'informatica scientifica con strumenti open source

Storicamente, la scienza computazionale è stata in gran parte confinata al regno dei ricercatori e dei dottorandi. Tuttavia, nel corso degli anni, forse all'insaputa della più ampia comunità di software, noi teste d'uovo di informatica scientifica abbiamo compilato silenziosamente librerie open-source collaborative che gestiscono la stragrande maggioranza del lavoro pesante . Il risultato è che ora è più facile che mai implementare modelli matematici e, mentre il campo potrebbe non essere ancora pronto per il consumo di massa, il livello di successo dell'implementazione è stato drasticamente abbassato. Lo sviluppo di una nuova base di codice computazionale da zero è un'impresa enorme, misurata in genere in anni, ma questi progetti di calcolo scientifico open source stanno rendendo possibile l'esecuzione con esempi accessibili per sfruttare in modo relativamente rapido queste capacità di calcolo.

Poiché lo scopo del calcolo scientifico è quello di fornire informazioni scientifiche sui sistemi reali che esistono in natura, la disciplina rappresenta l'avanguardia nel fare in modo che il software per computer si avvicini alla realtà. Per realizzare un software che imiti il ​​mondo reale a un livello molto elevato sia di accuratezza che di risoluzione, è necessario invocare la matematica differenziale complessa, che richiede conoscenze che raramente si trovano oltre le mura delle università, dei laboratori nazionali o dei dipartimenti di ricerca e sviluppo aziendali. Inoltre, si presentano sfide numeriche significative quando si tenta di descrivere il tessuto continuo e infinitesimale del mondo reale usando il linguaggio discreto degli zeri e degli uno. Uno sforzo esauriente di un'attenta trasformazione numerica è necessario per rendere algoritmi che siano sia computazionalmente trattabili, sia che diano risultati significativi. In altre parole, l'informatica scientifica è pesante.

Strumenti open source per l'informatica scientifica

Personalmente sono particolarmente affezionato al progetto FEniCS, lo utilizzo per il mio lavoro di tesi, e dimostrerò la mia propensione a selezionarlo per il nostro esempio di codice per questo tutorial. (Ci sono altri progetti di altissima qualità come DUNE che si potrebbero usare anche.)

FEniCS si autodefinisce come "un progetto collaborativo per lo sviluppo di concetti e strumenti innovativi per il calcolo scientifico automatizzato, con un focus particolare sulla soluzione automatizzata di equazioni differenziali mediante metodi agli elementi finiti". Questa è una potente libreria per risolvere una vasta gamma di problemi e applicazioni di calcolo scientifico. I suoi contributori includono Simula Research Laboratory, l'Università di Cambridge, l'Università di Chicago, la Baylor University e il KTH Royal Institute of Technology, che collettivamente lo hanno trasformato in una risorsa inestimabile nel corso dell'ultimo decennio (vedi FEniCS codeswarm).

Ciò che è piuttosto sorprendente è lo sforzo da cui la libreria FEniCS ci ha protetto. Per avere un'idea dell'incredibile profondità e ampiezza degli argomenti trattati dal progetto, è possibile visualizzare il loro libro di testo open source, in cui il Capitolo 21 confronta anche vari schemi agli elementi finiti per la risoluzione di flussi incomprimibili.

Dietro le quinte il progetto ha integrato per noi un ampio set di librerie di calcolo scientifico open source, che possono essere di interesse o di utilizzo diretto. Questi includono, in ordine sparso, i progetti che il progetto FEniCS richiama:

• PETSc: una suite di strutture dati e routine per la soluzione scalabile (parallela) di applicazioni scientifiche modellate da equazioni differenziali alle derivate parziali.
• Progetto Trilinos: un insieme di algoritmi e tecnologie robusti per la risoluzione di equazioni sia lineari che non lineari, sviluppato dal lavoro presso i Sandia National Labs.
• uBLAS: "Una libreria di classi di modelli C++ che fornisce funzionalità BLAS di livello 1, 2, 3 per matrici dense, impacchettate e sparse e molti algoritmi numerici per l'algebra lineare".
• GMP: una libreria gratuita per l'aritmetica di precisione arbitraria, che opera su interi con segno, numeri razionali e numeri in virgola mobile.
• UMFPACK: un insieme di routine per la risoluzione di sistemi lineari sparsi asimmetrici, Ax=b, utilizzando il metodo Unsymmetric MultiFrontal.
• ParMETIS: una libreria parallela basata su MPI che implementa una varietà di algoritmi per il partizionamento di grafici non strutturati, mesh e per il calcolo degli ordinamenti di riduzione del riempimento di matrici sparse.
• NumPy: il pacchetto fondamentale per il calcolo scientifico con Python.
• CGAL: algoritmi geometrici efficienti e affidabili sotto forma di libreria C++.
• SCOTCH: Un pacchetto software e librerie per il partizionamento di grafi sequenziali e paralleli, la mappatura statica e il clustering, il partizionamento sequenziale di mesh e ipergrafi e l'ordinamento di blocchi di matrice sparsa sequenziale e parallelo.
• MPI: un sistema di passaggio messaggi standardizzato e portatile progettato da un gruppo di ricercatori del mondo accademico e industriale per funzionare su un'ampia varietà di computer paralleli.
• VTK: un sistema software open source disponibile gratuitamente per la computer grafica 3D, l'elaborazione e la visualizzazione delle immagini.
• SLEPc: una libreria software per la soluzione di problemi di autovalori sparsi su larga scala su computer paralleli.

Questo elenco di pacchetti esterni integrati nel progetto ci dà un'idea delle sue capacità ereditate. Ad esempio, il supporto integrato per MPI consente la scalabilità tra i lavoratori remoti in un ambiente di cluster di elaborazione (ad esempio, questo codice verrà eseguito su un super computer o sul tuo laptop).

È anche interessante notare che ci sono molte applicazioni oltre al calcolo scientifico per le quali questi progetti potrebbero essere utilizzati, inclusi modelli finanziari, elaborazione delle immagini, problemi di ottimizzazione e forse anche videogiochi. Sarebbe possibile, ad esempio, creare un videogioco che utilizzi alcuni di questi algoritmi e tecniche open source per risolvere il flusso di un fluido bidimensionale, come quello delle correnti oceaniche/fiume con cui un giocatore interagirebbe (forse provare a navigare una barca con vento e flussi d'acqua variabili).

Un'applicazione di esempio: sfruttare l'open source per l'informatica scientifica

Qui cercherò di dare un'idea di cosa comporta lo sviluppo di un modello numerico, mostrando come uno schema di base di fluidodinamica computazionale viene sviluppato e implementato in una di queste librerie open source - in questo caso il progetto FEniCS. FEnICS fornisce API sia in Python che in C++. Per questo esempio, useremo la loro API Python.

Discuteremo alcuni contenuti piuttosto tecnici, ma l'obiettivo sarà semplicemente quello di dare un assaggio di cosa comporta lo sviluppo di tale codice di calcolo scientifico e quanto lavoro fanno per noi gli strumenti open source di oggi. Nel processo, speriamo di aiutare a demistificare il complesso mondo dell'informatica scientifica. (Si noti che viene fornita un'appendice che dettaglia tutte le basi matematiche e scientifiche per coloro che sono interessati a quel livello di dettaglio.)

DISCLAIMER: per quei lettori con poca o nessuna esperienza in software e applicazioni di calcolo scientifico, parti di questo esempio potrebbero farti sentire così:

Se è così, non disperare. Il punto principale qui è la misura in cui i progetti open source esistenti possono semplificare notevolmente molte di queste attività.

Con questo in mente, iniziamo guardando la demo FEnICS per Navier-Stokes incomprimibili. Questa demo modella la pressione e la velocità di un fluido incomprimibile che scorre attraverso una curva a forma di L, come un tubo idraulico.

La descrizione nella pagina demo collegata fornisce un'eccellente e concisa configurazione dei passaggi necessari per eseguire il codice e ti incoraggio a dare una rapida occhiata per vedere cosa è coinvolto. Per riassumere, la demo risolverà la velocità e la pressione attraverso la curva per le equazioni del flusso incomprimibile. La demo esegue una breve simulazione del fluido che scorre nel tempo, animando i risultati man mano che procede. Ciò si ottiene impostando la mesh che rappresenta lo spazio nel tubo e utilizzando il metodo degli elementi finiti per risolvere numericamente la velocità e la pressione in ciascun punto della mesh. Quindi ripetiamo nel tempo, aggiornando i campi di velocità e pressione mentre procediamo, usando ancora le equazioni che abbiamo a nostra disposizione.

La demo funziona bene così com'è, ma la modificheremo leggermente. La demo utilizza lo split Chorin, ma utilizzeremo invece il metodo leggermente diverso ispirato a Kim e Moin, che speriamo sia più stabile. Ciò richiede solo di modificare l'equazione utilizzata per approssimare i termini convettivi e viscosi, ma per farlo è necessario memorizzare il campo di velocità del passaggio temporale precedente e aggiungere due termini aggiuntivi all'equazione di aggiornamento, che utilizzerà quella precedente informazioni per un'approssimazione numerica più accurata.

Quindi facciamo questo cambiamento. Innanzitutto, aggiungiamo un nuovo oggetto Function al setup. Questo è un oggetto che rappresenta una funzione matematica astratta come un vettore o un campo scalare. Lo chiameremo un1 , memorizzerà il campo di velocità precedente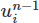 sul nostro spazio funzionale V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

Successivamente, dobbiamo cambiare il modo in cui la "velocità provvisoria" viene aggiornata durante ogni fase della simulazione. Questo campo rappresenta la velocità approssimata nella fase successiva in cui la pressione viene ignorata (a questo punto la pressione non è ancora nota). È qui che sostituiamo il metodo della divisione Chorin con il più recente metodo del passo frazionario di Kim e Moin. In altre parole, cambieremo l'espressione per il campo F1 :

Sostituire:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

Insieme a:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

in modo che la demo ora utilizzi il nostro metodo aggiornato per risolvere il campo della velocità intermedia quando utilizza F1 .

Infine, assicurati di aggiornare il campo di velocità precedente, un1 , alla fine di ogni passaggio dell'iterazione

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

In modo che quello che segue sia il codice completo della nostra demo FEniCS CFD, con le nostre modifiche incluse:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

L'esecuzione del programma mostra il flusso intorno al gomito. Esegui tu stesso il codice di calcolo scientifico per vederlo animato! Le schermate del frame finale sono presentate di seguito.

Pressioni relative nella curva al termine della simulazione, scalate e colorate per grandezza (valori non dimensionali):

Velocità relative nella curva alla fine della simulazione come glifi vettoriali scalati e colorati in base alla grandezza (valori non dimensionali).

Quindi quello che abbiamo fatto è stato prendere una demo esistente, che per caso implementa uno schema molto simile al nostro piuttosto facilmente, e l'abbiamo modificata per usare approssimazioni migliori usando le informazioni del passaggio temporale precedente.

A questo punto potresti pensare che fosse una modifica banale. Lo era, ed è in gran parte questo il punto. Questo progetto di calcolo scientifico open source ci ha permesso di implementare rapidamente un modello numerico modificato modificando quattro righe di codice. Tali modifiche possono richiedere mesi nei codici di ricerca di grandi dimensioni.

Il progetto ha molte altre demo che potrebbero essere utilizzate come punto di partenza. Ci sono anche un certo numero di applicazioni open source costruite sul progetto che implementano vari modelli.

Conclusione

L'informatica scientifica e le sue applicazioni sono davvero complesse. Non c'è niente da fare. Ma come è sempre più vero in così tanti domini, il panorama sempre crescente di strumenti e progetti open source disponibili può semplificare notevolmente quelle che altrimenti sarebbero attività di programmazione estremamente complicate e noiose. E forse è anche vicino il momento in cui l'informatica scientifica diventa abbastanza accessibile da trovarsi prontamente utilizzata al di fuori della comunità di ricerca.

APPENDICE: Basi scientifiche e matematiche

Per gli interessati, ecco le basi tecniche della nostra guida sulla dinamica dei fluidi computazionale sopra. Quello che segue servirà come un riassunto molto utile e conciso di argomenti che sono tipicamente trattati nel corso di una dozzina di corsi di livello universitario. Studenti laureati e tipi matematici interessati a una profonda comprensione dell'argomento possono trovare questo materiale piuttosto coinvolgente.

Meccanica dei fluidi

La "modellazione", in generale, è il processo di risoluzione di un sistema reale con approssimazioni in serie. Il modello, spesso, coinvolgerà equazioni continue inadatte per l'implementazione al computer, e quindi deve essere ulteriormente approssimato con metodi numerici.

Per la meccanica dei fluidi, iniziamo questa guida dalle equazioni fondamentali, le equazioni di Navier-Stokes, e usiamole per sviluppare uno schema CFD.

Le equazioni di Navier-Stokes sono una serie di equazioni alle derivate parziali (PDE) che descrivono molto bene i flussi di fluido e sono quindi il nostro punto di partenza. Possono essere derivati ​​da leggi di conservazione di massa, quantità di moto ed energia lanciate attraverso un teorema di trasporto di Reynolds e applicando il teorema di Gauss e invocando l'ipotesi di Stoke. Le equazioni richiedono un'assunzione del continuo, in cui si presume che abbiamo abbastanza particelle fluide per fornire proprietà statistiche come temperatura, densità e significato di velocità. Inoltre, sono necessarie una relazione lineare tra il tensore della sollecitazione superficiale e il tensore della velocità di deformazione, la simmetria nel tensore della sollecitazione e le ipotesi del fluido isotropo. È importante conoscere le ipotesi che facciamo ed ereditiamo durante questo sviluppo in modo da poter valutare l'applicabilità nel codice risultante. Le equazioni di Navier-Stokes nella notazione di Einstein, senza ulteriori indugi:

Conservazione di massa:

Conservazione della quantità di moto:

Conservazione dell'energia:

dove lo stress deviatorico è:

Sebbene siano molto generali, governino la maggior parte dei flussi di fluidi nel mondo fisico, non sono direttamente di grande utilità. Ci sono relativamente poche soluzioni esatte note alle equazioni e un Millennium Prize di $ 1.000.000 è disponibile per chiunque possa risolvere il problema dell'esistenza e della scorrevolezza. La parte importante è che abbiamo un punto di partenza per lo sviluppo del nostro modello facendo una serie di ipotesi per ridurre la complessità (sono alcune delle equazioni più difficili della fisica classica).

Per mantenere le cose "semplici" utilizzeremo la nostra conoscenza specifica del dominio per fare un'ipotesi incomprimibile sul fluido e assumere temperature costanti in modo tale che l'equazione di conservazione dell'energia, che diventa l'equazione del calore, non sia necessaria (disaccoppiata). Ora abbiamo due equazioni, sempre PDE, ma significativamente più semplici pur risolvendo un gran numero di problemi di fluidi reali.

Equazione di continuità

Equazioni della quantità di moto

A questo punto abbiamo ora un bel modello matematico per i flussi di fluidi incomprimibili (gas e liquidi a bassa velocità come l'acqua, per esempio). Risolvere queste equazioni direttamente a mano non è facile, ma è bello in quanto possiamo ottenere soluzioni “esatte” per problemi semplici. L'uso di queste equazioni per affrontare problemi di interesse, ad esempio l'aria che scorre sopra un'ala o l'acqua che scorre attraverso un sistema, richiede la risoluzione di queste equazioni numericamente.

Costruire uno schema numerico

Per risolvere problemi più complessi utilizzando il computer, è necessario un metodo per risolvere numericamente le nostre equazioni incomprimibili. Risolvere numericamente equazioni differenziali alle derivate parziali, o anche equazioni differenziali, non è banale. Tuttavia, le nostre equazioni in questa guida presentano una sfida particolare (sorpresa!). Cioè, dobbiamo risolvere le equazioni della quantità di moto mantenendo la soluzione libera dalla divergenza, come richiesto dalla continuità. Una semplice integrazione temporale attraverso qualcosa come il metodo Runge-Kutta è resa difficile poiché l'equazione di continuità non ha una derivata temporale al suo interno.

Non esiste un metodo corretto, o addirittura migliore, per risolvere le equazioni, ma ci sono molte opzioni praticabili. Nel corso dei decenni sono stati trovati diversi approcci per affrontare il problema, come la riformulazione in termini di vorticità e funzione di flusso, l'introduzione della comprimibilità artificiale e la divisione dell'operatore. Chorin (1969), e poi Kim e Moin (1984, 1990), hanno formulato un metodo a gradino frazionario molto popolare e di grande successo che ci consentirà di integrare le equazioni risolvendo il campo di pressione direttamente, piuttosto che implicitamente. Il metodo del passo frazionario è un metodo generale per approssimare le equazioni suddividendo i loro operatori, in questo caso suddividendo lungo la pressione. L'approccio è relativamente semplice e tuttavia robusto, motivando la sua scelta qui.

In primo luogo, dobbiamo discriminare numericamente le equazioni nel tempo in modo da poter passare da un momento all'altro. Seguendo Kim e Moin (1984), useremo il metodo di Adams-Bashforth esplicito del secondo ordine per i termini convettivi, il metodo di Crank-Nicholson implicito del secondo ordine per i termini viscosi, una semplice differenza finita per la derivata temporale , trascurando il gradiente di pressione. Queste scelte non sono affatto le uniche approssimazioni che si possono fare: la loro selezione fa parte dell'arte nella costruzione dello schema controllando il comportamento numerico dello schema.

La velocità intermedia ora può essere integrata, tuttavia, ignora il contributo della pressione ed è ora divergente (l'incomprimibilità richiede che sia priva di divergenza). Il resto dell'operatore è necessario per portarci alla fase successiva.

dove è uno scalare che dobbiamo trovare che si traduce in una velocità libera divergente. Possiamo trovare prendendo la divergenza della fase di correzione,

dove il primo termine è zero come richiesto dalla continuità, producendo un'equazione di Poisson per un campo scalare che fornirà una velocità solenoidale (libera divergente) al passo temporale successivo.

Come mostrano Kim e Moin (1984), non è esattamente la pressione a seguito della scissione dell'operatore, ma può essere trovata da

A questo punto del tutorial stiamo andando piuttosto bene, abbiamo temporalmente discritizzato le equazioni governanti in modo da poterle integrare. Ora dobbiamo discriminare spazialmente gli operatori. Esistono numerosi metodi con cui potremmo ottenere ciò, ad esempio il metodo degli elementi finiti, il metodo dei volumi finiti e il metodo delle differenze finite. Nel lavoro originale di Kim e Moin (1984), si procede con il metodo delle differenze finite. Il metodo è vantaggioso per la sua relativa semplicità ed efficienza computazionale, ma soffre di geometrie complesse poiché richiede una mesh strutturata.

Il metodo degli elementi finiti (FEM) è una scelta conveniente per la sua generalità e ha alcuni bei progetti open source che aiutano nel suo utilizzo. In particolare gestisce geometrie reali in una, due e tre dimensioni, scale per problemi molto grandi su gruppi di macchine ed è relativamente facile da usare per elementi di ordine elevato. In genere il metodo è il più lento dei tre, tuttavia ci darà il maggior numero di chilometri attraverso i problemi, quindi lo useremo qui.

Anche quando si implementa la FEM ci sono molte scelte. Qui useremo il Galerkin FEM. In tal modo, trasformiamo le equazioni in forma residua ponderata moltiplicandole ciascuna per una funzione di test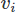 per i vettori e 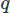per il campo scalare e l'integrazione nel dominio 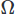. Eseguiamo quindi un'integrazione parziale su qualsiasi derivata di ordine elevato utilizzando il teorema di Stoke o il teorema di Divergenza. Quindi poniamo il problema variazionale, ottenendo il nostro schema CFD desiderato.

Ora abbiamo un bel schema matematico in una forma "conveniente" per l'implementazione, si spera con un certo senso di ciò che era necessario per arrivarci (molta matematica e metodi di brillanti ricercatori che praticamente copiamo e modifichiamo).