Panduan untuk Komputasi Ilmiah dengan Alat Sumber Terbuka

Secara historis, ilmu komputasi sebagian besar terbatas pada bidang ilmuwan penelitian dan kandidat doktor. Namun, selama bertahun-tahun – mungkin tanpa sepengetahuan komunitas perangkat lunak yang lebih besar – kami para ilmuwan komputasi ilmiah telah diam-diam menyusun perpustakaan sumber terbuka kolaboratif yang menangani sebagian besar pekerjaan berat . Hasilnya adalah sekarang lebih mudah dari sebelumnya untuk mengimplementasikan model matematika, dan sementara lapangan mungkin belum siap untuk konsumsi massal, hambatan untuk implementasi yang sukses telah diturunkan secara drastis. Mengembangkan basis kode komputasi baru dari awal adalah tugas besar, biasanya diukur dalam beberapa tahun, tetapi proyek komputasi ilmiah open source ini memungkinkan untuk dijalankan dengan contoh yang dapat diakses untuk secara relatif cepat memanfaatkan kemampuan komputasi ini.

Karena tujuan komputasi ilmiah adalah untuk memberikan wawasan ilmiah ke dalam sistem nyata yang ada di alam, disiplin ini mewakili ujung tombak dalam membuat perangkat lunak komputer mendekati kenyataan. Untuk membuat perangkat lunak yang meniru dunia nyata dengan tingkat akurasi dan resolusi yang sangat tinggi, matematika diferensial yang kompleks harus digunakan, membutuhkan pengetahuan yang jarang ditemukan di luar tembok universitas, laboratorium nasional, atau departemen R&D perusahaan. Di atas semua ini, tantangan numerik yang signifikan muncul dengan sendirinya ketika mencoba untuk menggambarkan jalinan dunia nyata yang sangat kecil dan berkelanjutan menggunakan bahasa diskrit nol dan satu. Upaya menyeluruh dari transformasi numerik yang cermat diperlukan untuk membuat algoritme yang dapat secara komputasional dapat dilacak, dan yang memberikan hasil yang berarti. Dengan kata lain, komputasi ilmiah adalah tugas berat.

Alat Sumber Terbuka untuk Komputasi Ilmiah

Saya pribadi sangat menyukai proyek FEniCS, menggunakannya untuk tugas tesis saya, dan akan menunjukkan bias saya dalam memilihnya untuk contoh kode kami untuk tutorial ini. (Ada proyek berkualitas sangat tinggi lainnya seperti DUNE yang dapat digunakan juga.)

FEniCS digambarkan sebagai "proyek kolaboratif untuk pengembangan konsep dan alat inovatif untuk komputasi ilmiah otomatis, dengan fokus khusus pada solusi otomatis persamaan diferensial dengan metode elemen hingga." Ini adalah perpustakaan yang kuat untuk memecahkan sejumlah besar masalah dan aplikasi komputasi ilmiah. Kontributornya termasuk Simula Research Laboratory, University of Cambridge, University of Chicago, Baylor University, dan KTH Royal Institute of Technology, yang secara kolektif telah membangunnya menjadi sumber daya yang tak ternilai selama dekade terakhir (lihat FEniCS codewarm).

Yang agak mencengangkan adalah seberapa banyak upaya yang telah dilakukan perpustakaan FEniCS untuk melindungi kami. Untuk memahami kedalaman dan luasnya topik yang dicakup proyek, seseorang dapat melihat buku teks open source mereka, di mana Bab 21 bahkan membandingkan berbagai skema elemen hingga untuk menyelesaikan aliran yang tidak dapat dimampatkan.

Di balik layar, proyek ini telah mengintegrasikan bagi kami sekumpulan besar perpustakaan komputasi ilmiah sumber terbuka, yang mungkin menarik atau berguna secara langsung. Ini termasuk, tanpa urutan tertentu, proyek-proyek yang disebut oleh proyek FEniCS:

• PETSc: Serangkaian struktur data dan rutinitas untuk solusi skalabel (paralel) dari aplikasi ilmiah yang dimodelkan oleh persamaan diferensial parsial.
• Proyek Trilinos: Serangkaian algoritme dan teknologi yang kuat untuk menyelesaikan persamaan linier dan non-linier, dikembangkan dari pekerjaan di Sandia National Labs.
• uBLAS: “Perpustakaan kelas template C++ yang menyediakan fungsionalitas BLAS level 1, 2, 3 untuk matriks padat, padat, dan jarang serta banyak algoritme numerik untuk aljabar linier.”
• GMP: Pustaka gratis untuk aritmatika presisi arbitrer, beroperasi pada bilangan bulat bertanda, bilangan rasional, dan bilangan floating-point.
• UMFPACK: Serangkaian rutinitas untuk menyelesaikan sistem linier jarang tidak simetris, Ax=b, menggunakan metode MultiFrontal Tidak simetris.
• ParMETIS: Pustaka paralel berbasis MPI yang mengimplementasikan berbagai algoritme untuk mempartisi graf tidak terstruktur, mesh, dan untuk menghitung urutan pengurangan isi dari matriks sparse.
• NumPy: Paket dasar untuk komputasi ilmiah dengan Python.
• CGAL: Algoritme geometri yang efisien dan andal dalam bentuk pustaka C++.
• SCOTCH: Paket perangkat lunak dan pustaka untuk partisi grafik sekuensial dan paralel, pemetaan dan pengelompokan statis, partisi mesh dan hypergraph sekuensial, dan pemesanan blok matriks sparse sekuensial dan paralel.
• MPI: Sistem pengiriman pesan standar dan portabel yang dirancang oleh sekelompok peneliti dari akademisi dan industri untuk berfungsi pada berbagai macam komputer paralel.
• VTK: Sistem perangkat lunak sumber terbuka yang tersedia secara bebas untuk grafik komputer 3D, pemrosesan gambar, dan visualisasi.
• SLEPc: Pustaka perangkat lunak untuk solusi masalah nilai eigen sparse skala besar pada komputer paralel.

Daftar paket eksternal yang terintegrasi ke dalam proyek ini memberi kita gambaran tentang kemampuan yang diwarisinya. Misalnya, memiliki dukungan terintegrasi untuk MPI memungkinkan penskalaan di seluruh pekerja jarak jauh di lingkungan klaster komputasi (yaitu, kode ini akan berjalan di komputer super atau laptop Anda).

Menarik juga untuk dicatat bahwa ada banyak aplikasi di luar komputasi ilmiah yang dapat dimanfaatkan oleh proyek-proyek ini, termasuk pemodelan keuangan, pemrosesan gambar, masalah pengoptimalan, dan bahkan mungkin video game. Mungkin saja, misalnya, untuk membuat video game yang menggunakan beberapa algoritme dan teknik sumber terbuka ini untuk memecahkan aliran fluida dua dimensi, seperti arus laut/sungai yang akan berinteraksi dengan pemain (mungkin coba dan mengarungi perahu dengan berbagai aliran angin dan air).

Contoh Aplikasi: Memanfaatkan Open Source untuk Komputasi Ilmiah

Di sini saya akan mencoba memberikan gambaran tentang apa yang melibatkan pengembangan model numerik dengan menunjukkan bagaimana skema dasar Dinamika Fluida Komputasi dikembangkan dan diimplementasikan di salah satu perpustakaan sumber terbuka ini - dalam hal ini proyek FEniCS. FEnICS menyediakan API dalam Python dan C++. Untuk contoh ini, kami akan menggunakan API Python mereka.

Kami akan membahas beberapa konten yang agak teknis, tetapi tujuannya hanya untuk memberikan gambaran tentang pengembangan kode komputasi ilmiah semacam itu, dan seberapa banyak kerja keras yang dilakukan alat open source saat ini bagi kami. Dalam prosesnya, semoga kami akan membantu mengungkap dunia komputasi ilmiah yang kompleks. (Perhatikan bahwa Lampiran disediakan yang merinci semua dasar matematika dan ilmiah bagi mereka yang tertarik pada tingkat detail itu.)

PENOLAKAN: Bagi pembaca dengan sedikit atau tanpa latar belakang dalam perangkat lunak dan aplikasi komputasi ilmiah, bagian dari contoh ini mungkin membuat Anda merasa seperti ini:

Jika demikian, jangan putus asa. Takeaway utama di sini adalah sejauh mana proyek open source yang ada dapat sangat menyederhanakan banyak tugas ini.

Dengan mengingat hal itu, mari kita mulai dengan melihat demo FEnICS untuk Navier-Stokes yang tidak dapat dimampatkan. Demo ini memodelkan tekanan dan kecepatan fluida yang tidak dapat dimampatkan yang mengalir melalui tikungan berbentuk L, seperti pipa ledeng.

Deskripsi pada halaman demo tertaut memberikan pengaturan yang sangat baik dan ringkas tentang langkah-langkah yang diperlukan untuk menjalankan kode, dan saya mendorong Anda untuk melihat sekilas untuk melihat apa yang terlibat. Untuk meringkas, demo akan memecahkan kecepatan dan tekanan melalui tikungan untuk persamaan aliran mampat. Demo menjalankan simulasi singkat dari cairan yang mengalir dari waktu ke waktu, menganimasikan hasil saat berjalan. Hal ini dicapai dengan mengatur mesh yang mewakili ruang di dalam pipa, dan menggunakan Metode Elemen Hingga untuk memecahkan secara numerik kecepatan dan tekanan pada setiap titik pada mesh. Kami kemudian mengulangi waktu, memperbarui bidang kecepatan dan tekanan saat kami pergi, sekali lagi menggunakan persamaan yang kami miliki.

Demo berfungsi dengan baik apa adanya, tetapi kami akan sedikit memodifikasinya. Demo ini menggunakan Chorin split, tetapi kami akan menggunakan metode yang sedikit berbeda yang terinspirasi oleh Kim dan Moin, yang kami harap lebih stabil. Ini hanya mengharuskan kita untuk mengubah persamaan yang digunakan untuk memperkirakan suku konvektif dan kental, tetapi untuk melakukannya kita perlu menyimpan medan kecepatan dari langkah waktu sebelumnya, dan menambahkan dua suku tambahan ke persamaan pembaruan, yang akan menggunakan persamaan sebelumnya informasi untuk perkiraan numerik yang lebih akurat.

Jadi mari kita lakukan perubahan ini. Pertama, kami menambahkan objek Function baru ke pengaturan. Ini adalah objek yang mewakili fungsi matematika abstrak seperti bidang vektor atau skalar. Kami akan menyebutnya un1 itu akan menyimpan medan kecepatan sebelumnya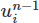 pada ruang fungsi kita V .

 ... # Create functions (three distinct vector fields and a scalar field) un1 = Function(V) # the previous time step's velocity field we are adding u0 = Function(V) # the current velocity field u1 = Function(V) # the next velocity field (what's being solved for) p1 = Function(Q) # the next pressure field (what's being solved for) ...

Selanjutnya, kita perlu mengubah cara "kecepatan tentatif" diperbarui selama setiap langkah simulasi. Bidang ini mewakili kecepatan yang diperkirakan pada langkah waktu berikutnya ketika tekanan diabaikan (pada titik ini tekanan belum diketahui). Di sinilah kami mengganti metode pemisahan Chorin dengan metode langkah fraksional Kim dan Moin yang lebih baru. Dengan kata lain, kita akan mengubah ekspresi untuk field F1 :

Mengganti:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Chorin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ inner(grad(u0)*u0, v)*dx + \ nu*inner(grad(u), grad(v))*dx - \ inner(f, v)*dx

Dengan:

 # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx

sehingga demo sekarang menggunakan metode terbaru kami untuk menyelesaikan medan kecepatan menengah saat menggunakan F1 .

Terakhir, pastikan kita memperbarui bidang kecepatan sebelumnya, un1 , di akhir setiap langkah iterasi

 ... # Move to next time step un1.assign(u0) # copy the current velocity field into the previous velocity field u0.assign(u1) # copy the next velocity field into the current velocity field ...

Sehingga berikut kode lengkap dari demo CFD FEniCS kami, dengan perubahan yang kami lakukan antara lain:

 """This demo program solves the incompressible Navier-Stokes equations on an L-shaped domain using Kim and Moin's fractional step method.""" # Begin demo from dolfin import * # Print log messages only from the root process in parallel parameters["std_out_all_processes"] = False; # Load mesh from file mesh = Mesh("lshape.xml.gz") # Define function spaces (P2-P1) V = VectorFunctionSpace(mesh, "Lagrange", 2) Q = FunctionSpace(mesh, "Lagrange", 1) # Define trial and test functions u = TrialFunction(V) p = TrialFunction(Q) v = TestFunction(V) q = TestFunction(Q) # Set parameter values dt = 0.01 T = 3 nu = 0.01 # Define time-dependent pressure boundary condition p_in = Expression("sin(3.0*t)", t=0.0) # Define boundary conditions noslip = DirichletBC(V, (0, 0), "on_boundary && \ (x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ (x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") bcu = [noslip] bcp = [inflow, outflow] # Create functions un1 = Function(V) u0 = Function(V) u1 = Function(V) p1 = Function(Q) # Define coefficients k = Constant(dt) f = Constant((0, 0)) # Tentative velocity field (a first prediction of what the next velocity field is) # for the Kim and Moin style split # F1 = change in the velocity field + # convective term + # diffusive term - # body force term F1 = (1/k)*inner(u - u0, v)*dx + \ (3.0/2.0) * inner(grad(u0)*u0, v)*dx - (1.0/2.0) * inner(grad(un1)*un1, v)*dx + \ (nu/2.0)*inner(grad(u+u0), grad(v))*dx - \ inner(f, v)*dx a1 = lhs(F1) L1 = rhs(F1) # Pressure update a2 = inner(grad(p), grad(q))*dx L2 = -(1/k)*div(u1)*q*dx # Velocity update a3 = inner(u, v)*dx L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx # Assemble matrices A1 = assemble(a1) A2 = assemble(a2) A3 = assemble(a3) # Use amg preconditioner if available prec = "amg" if has_krylov_solver_preconditioner("amg") else "default" # Create files for storing solution ufile = File("results/velocity.pvd") pfile = File("results/pressure.pvd") # Time-stepping t = dt while t < T + DOLFIN_EPS: # Update pressure boundary condition p_in.t = t # Compute tentative velocity step begin("Computing tentative velocity") b1 = assemble(L1) [bc.apply(A1, b1) for bc in bcu] solve(A1, u1.vector(), b1, "gmres", "default") end() # Pressure correction begin("Computing pressure correction") b2 = assemble(L2) [bc.apply(A2, b2) for bc in bcp] solve(A2, p1.vector(), b2, "cg", prec) end() # Velocity correction begin("Computing velocity correction") b3 = assemble(L3) [bc.apply(A3, b3) for bc in bcu] solve(A3, u1.vector(), b3, "gmres", "default") end() # Plot solution plot(p1, title="Pressure", rescale=True) plot(u1, title="Velocity", rescale=True) # Save to file ufile << u1 pfile << p1 # Move to next time step un1.assign(u0) u0.assign(u1) t += dt print "t =", t # Hold plot interactive()

Menjalankan program menunjukkan aliran di sekitar siku. Jalankan sendiri kode komputasi ilmiah untuk melihatnya bernyawa! Layar dari bingkai terakhir disajikan di bawah ini.

Tekanan relatif di tikungan pada akhir simulasi, diskalakan dan diwarnai dengan besaran (nilai non-dimensi):

Kecepatan relatif di tikungan pada akhir simulasi sebagai mesin terbang vektor diskalakan dan diwarnai oleh besarnya (nilai non-dimensi).

Jadi apa yang telah kami lakukan adalah mengambil demo yang ada, yang kebetulan menerapkan skema yang sangat mirip dengan kami dengan mudah, dan memodifikasinya untuk menggunakan perkiraan yang lebih baik dengan menggunakan informasi dari langkah waktu sebelumnya.

Pada titik ini Anda mungkin berpikir bahwa itu adalah editan yang sepele. Itu, dan itu sebagian besar intinya. Proyek komputasi ilmiah open source ini memungkinkan kami untuk dengan cepat menerapkan model numerik yang dimodifikasi dengan mengubah empat baris kode. Perubahan tersebut mungkin memakan waktu berbulan-bulan dalam kode penelitian besar.

Proyek ini memiliki banyak demo lain yang dapat digunakan sebagai titik awal. Bahkan ada sejumlah aplikasi open source yang dibangun di atas proyek yang mengimplementasikan berbagai model.

Kesimpulan

Komputasi ilmiah dan aplikasinya memang kompleks. Tidak ada cara untuk menghindarinya. Tetapi seperti yang semakin benar di banyak domain, lanskap yang terus berkembang dari alat dan proyek open source yang tersedia dapat secara signifikan menyederhanakan apa yang seharusnya menjadi tugas pemrograman yang sangat rumit dan membosankan. Dan mungkin waktunya sudah dekat di mana komputasi ilmiah menjadi cukup dapat diakses untuk menemukan dirinya siap digunakan di luar komunitas riset.

LAMPIRAN: Dasar-dasar Ilmiah dan Matematika

Bagi mereka yang tertarik, berikut adalah dasar-dasar teknis dari panduan Dinamika Fluida Komputasi kami di atas. Berikut ini akan berfungsi sebagai ringkasan topik yang sangat berguna dan ringkas yang biasanya dibahas selama selusin kursus tingkat pascasarjana. Mahasiswa pascasarjana dan tipe matematika yang tertarik pada pemahaman mendalam tentang topik ini mungkin menganggap materi ini cukup menarik.

Mekanika Fluida

"Pemodelan," secara umum, adalah proses penyelesaian beberapa sistem nyata dengan aproksimasi deret. Model, akan sering melibatkan persamaan kontinu yang tidak cocok untuk implementasi komputer, dan karenanya harus didekati lebih lanjut dengan metode numerik.

Untuk mekanika fluida, mari kita mulai panduan ini dari persamaan dasar, persamaan Navier-Stokes, dan menggunakannya untuk mengembangkan skema CFD.

Persamaan Navier-Stokes adalah serangkaian persamaan diferensial parsial (PDE) yang menggambarkan aliran fluida dengan sangat baik dan dengan demikian merupakan titik awal kami. Mereka dapat diturunkan dari hukum massa, momentum, dan kekekalan energi yang diberikan melalui Teorema Transportasi Reynolds dan menerapkan teorema Gauss dan menerapkan Hipotesis Stoke. Persamaan memerlukan asumsi kontinum, di mana diasumsikan kita memiliki partikel fluida yang cukup untuk memberikan sifat statistik seperti suhu, densitas dan makna kecepatan. Selain itu, hubungan linier antara tensor tegangan permukaan dan tensor laju regangan, simetri dalam tensor tegangan, dan asumsi fluida isotropik diperlukan. Penting untuk mengetahui asumsi yang kami buat dan mewarisi selama pengembangan ini sehingga kami dapat mengevaluasi penerapan dalam kode yang dihasilkan. Persamaan Navier-Stokes dalam notasi Einstein, tanpa basa-basi lagi:

Konservasi massa:

Kekekalan momentum:

Konservasi energi:

dimana tegangan deviatorik adalah:

Meskipun sangat umum, mengatur sebagian besar aliran fluida di dunia fisik, mereka tidak banyak digunakan secara langsung. Ada relatif sedikit solusi eksak yang diketahui untuk persamaan, dan Hadiah Milenium $1.000.000 ada di luar sana untuk siapa saja yang dapat memecahkan masalah keberadaan dan kelancaran. Bagian yang penting adalah kami memiliki titik awal untuk pengembangan model kami dengan membuat serangkaian asumsi untuk mengurangi kompleksitas (ini adalah beberapa persamaan tersulit dalam fisika klasik).

Untuk menjaga hal-hal "sederhana" kami akan menggunakan pengetahuan khusus domain kami untuk membuat asumsi termampatkan pada fluida, dan menganggap suhu konstan sehingga persamaan konservasi energi, yang menjadi persamaan panas, tidak diperlukan (dipisahkan). Kami sekarang memiliki dua persamaan, masih PDE, tetapi secara signifikan lebih sederhana sambil tetap menyelesaikan sejumlah besar masalah fluida nyata.

persamaan kontinuitas

Persamaan momentum

Pada titik ini kita sekarang memiliki model matematika yang bagus untuk aliran fluida yang tidak dapat dimampatkan (gas dan cairan berkecepatan rendah seperti air, misalnya). Memecahkan persamaan-persamaan ini secara langsung dengan tangan tidaklah mudah, tetapi menyenangkan karena kita dapat memperoleh solusi yang “tepat” untuk masalah-masalah sederhana. Menggunakan persamaan ini untuk mengatasi masalah yang menarik, katakanlah udara yang mengalir di atas sayap, atau air yang mengalir melalui beberapa sistem, mengharuskan kita menyelesaikan persamaan ini secara numerik.

Membangun Skema Numerik

Untuk menyelesaikan masalah yang lebih kompleks dengan menggunakan komputer, diperlukan metode untuk menyelesaikan persamaan inkompresibel secara numerik. Memecahkan persamaan diferensial parsial, atau bahkan persamaan diferensial, secara numerik bukanlah hal yang sepele. Namun, persamaan kami dalam panduan ini memiliki tantangan tertentu (kejutan!). Artinya, kita perlu menyelesaikan persamaan momentum sambil menjaga solusi divergensi bebas, seperti yang dipersyaratkan oleh kontinuitas. Integrasi waktu yang sederhana melalui sesuatu seperti metode Runge-Kutta menjadi sulit karena persamaan kontinuitas tidak memiliki turunan waktu di dalamnya.

Tidak ada metode yang benar, atau bahkan terbaik, untuk memecahkan persamaan, tetapi ada banyak pilihan yang bisa diterapkan. Selama beberapa dekade beberapa pendekatan telah ditemukan untuk mengatasi masalah ini, seperti merumuskan kembali dalam hal vortisitas dan fungsi aliran, memperkenalkan kompresibilitas buatan, dan pemisahan operator. Chorin (1969), dan kemudian Kim dan Moin (1984, 1990), merumuskan metode langkah pecahan yang sangat sukses dan populer yang akan memungkinkan kita untuk mengintegrasikan persamaan sambil memecahkan medan tekanan secara langsung, daripada secara implisit. Metode langkah fraksional adalah metode umum untuk pendekatan persamaan dengan membagi operatornya, dalam hal ini membelah sepanjang tekanan. Pendekatannya relatif sederhana namun kuat, memotivasi pilihannya di sini.

Pertama, kita perlu mendiskriminasi persamaan secara numerik dalam waktu sehingga kita dapat melangkah dari satu titik waktu ke titik berikutnya. Dalam mengikuti Kim dan Moin (1984), kami akan menggunakan metode Adams-Bashforth eksplisit orde kedua untuk suku konvektif, metode Crank-Nicholson implisit orde kedua untuk suku viskos, beda hingga sederhana untuk turunan waktu , sambil mengabaikan gradien tekanan. Pilihan-pilihan ini bukanlah satu-satunya perkiraan yang dapat dibuat: pemilihannya adalah bagian dari seni dalam membangun skema dengan mengontrol perilaku numerik skema.

Kecepatan menengah sekarang dapat diintegrasikan, namun mengabaikan kontribusi tekanan dan sekarang divergen (ketidakmampatan mengharuskannya bebas divergen). Sisa dari operator diperlukan untuk membawa kita ke langkah waktu berikutnya.

di mana adalah beberapa skalar kita perlu menemukan yang menghasilkan kecepatan bebas divergen. Kita dapat menemukan dengan mengambil divergensi langkah koreksi,

di mana suku pertama adalah nol seperti yang disyaratkan oleh kontinuitas, menghasilkan persamaan Poisson untuk medan skalar yang akan memberikan kecepatan solenoidal (bebas divergen) pada langkah waktu berikutnya.

Seperti yang ditunjukkan Kim dan Moin (1984), bukan tekanan sebagai akibat dari pemisahan operator, tetapi dapat ditemukan dengan

Pada titik ini dalam tutorial yang kami lakukan dengan cukup baik, kami telah mendiskriminasi sementara persamaan yang mengatur sehingga kami dapat mengintegrasikannya. Kita sekarang perlu mendiskriminasi operator secara spasial. Ada sejumlah metode yang dapat kita gunakan untuk mencapai ini, Metode Elemen Hingga, Metode Volume Hingga, dan Metode Beda Hingga, misalnya. Dalam karya asli Kim dan Moin (1984), mereka melanjutkan dengan Metode Beda Hingga. Metode ini menguntungkan untuk kesederhanaan relatif dan efisiensi komputasi, tetapi menderita untuk geometri yang kompleks karena memerlukan mesh terstruktur.

Metode Elemen Hingga (FEM) adalah pilihan yang nyaman untuk sifatnya yang umum dan memiliki beberapa proyek sumber terbuka yang sangat bagus yang membantu dalam penggunaannya. Secara khusus menangani geometri nyata dalam satu, dua dan tiga dimensi, skala untuk masalah yang sangat besar pada cluster mesin, dan relatif mudah digunakan untuk elemen orde tinggi. Biasanya metode ini lebih lambat dari ketiganya, namun itu akan memberi kita jarak tempuh paling banyak di seluruh masalah, jadi kita akan menggunakannya di sini.

Bahkan ketika menerapkan FEM ada banyak pilihan. Disini kita akan menggunakan FEM Galerkin. Dalam melakukannya, kami membuat persamaan dalam bentuk sisa tertimbang dengan mengalikan masing-masing dengan fungsi uji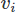 untuk vektor dan 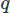untuk medan skalar, dan integrasikan pada domain 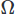. Kami kemudian melakukan integrasi parsial pada setiap turunan orde tinggi menggunakan teorema Stoke atau teorema Divergensi. Kami kemudian mengajukan masalah variasi, menghasilkan skema CFD yang kami inginkan.

Kami sekarang memiliki skema matematika yang bagus dalam bentuk "nyaman" untuk implementasi, semoga dengan beberapa pengertian tentang apa yang diperlukan untuk sampai ke sana (banyak matematika, dan metode dari peneliti brilian yang cukup banyak kami salin dan ubah).