預報員的工具箱：如何執行蒙特卡洛模擬

執行摘要

介紹

首先，唯一確定的是沒有確定性。 其次，作為結果的每一個決定都是權衡概率的問題。 第三，儘管存在不確定性，但我們必須做出決定並採取行動。 最後，我們不僅要根據結果來判斷決策，還要根據這些決策是如何做出的。 ——羅伯特·E·魯賓

預測中最重要和最具挑戰性的方面之一是處理檢查未來所固有的不確定性。 自 2003 年以來，我已經為 LBO、初創公司籌款、預算、併購和企業戰略計劃構建並填充了數百個財務和運營模型，我見證了這樣做的各種方法。 每個首席執行官、首席財務官、董事會成員、投資者或投資委員會成員都會在財務預測和不確定性方面帶來自己的經驗和方法——受不同激勵措施的影響。 通常，將實際結果與預測進行比較可以了解預測和實際結果之間的偏差有多大，因此需要理解和明確識別不確定性。

我最初開始使用情景和敏感性分析來模擬不確定性，並且仍然認為它們是非常有用的工具。 自從 2010 年將蒙特卡羅模擬添加到我的工具箱中以來，我發現它們是一種非常有效的工具，可以用來改進和改進您對風險和概率的看法。 從構建 DCF 估值、評估併購中的看漲期權、與貸方討論風險到尋求融資和指導初創企業的風險投資資金分配，我都使用了這種方法。 這種方法一直受到董事會成員、投資者和高級管理團隊的好評。 在本文中，我通過構建 DCF 估值模型提供了在實踐中使用蒙特卡羅模擬的分步教程。

每個決定都是權衡概率的問題

在開始案例研究之前，讓我們回顧一下處理不確定性的幾種不同方法。 預期價值的概念——所有可能情景中現金流的概率加權平均值——是財務 101。但財務專業人士和更廣泛的決策者在將這種簡單的見解轉化為實踐時採用了截然不同的方法。 該方法的範圍可以從一方面根本不承認或根本不討論不確定性，到另一方面複雜的模型和軟件。 在某些情況下，人們最終會花更多時間討論概率而不是計算現金流。

除了簡單地不解決它之外，讓我們研究一些在中長期預測中處理不確定性的方法。 您應該熟悉其中的許多內容。

創建一個場景。 這種方法是預算、許多初創公司甚至投資決策的默認方法。 除了不包含有關不確定程度的任何信息或承認結果可能與預測不同之外，它可能是模棱兩可的，並且根據利益相關者的不同解釋。 有些人可能會將其解釋為一個延伸目標，其中實際結果更有可能低於而不是超過。 一些人將其視為具有更多優勢而不是劣勢的基準性能。 其他人可能會將其視為上下概率為 50/50 的“基本案例”。 在某些方法中，尤其是對於初創公司來說，這是非常雄心勃勃的，到目前為止，失敗或不足的可能性更大，但是為了解釋風險，使用了更高的貼現率。	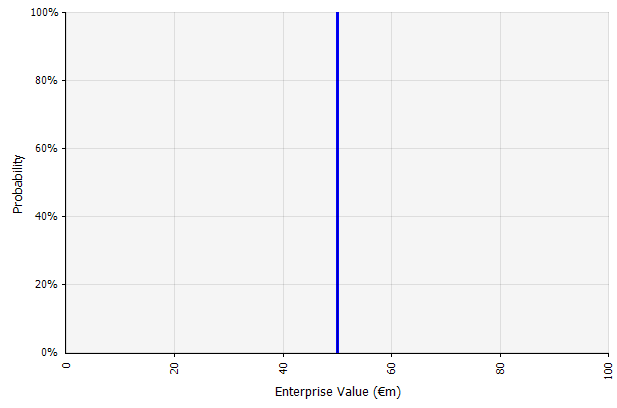這種方法下的長期現金流預測的輸入都是點估計，在這個例子中產生了 5000 萬歐元的點估計結果，隱含概率為 100%。
創建多個場景。 這種方法認識到現實不太可能按照一個給定的計劃展開。 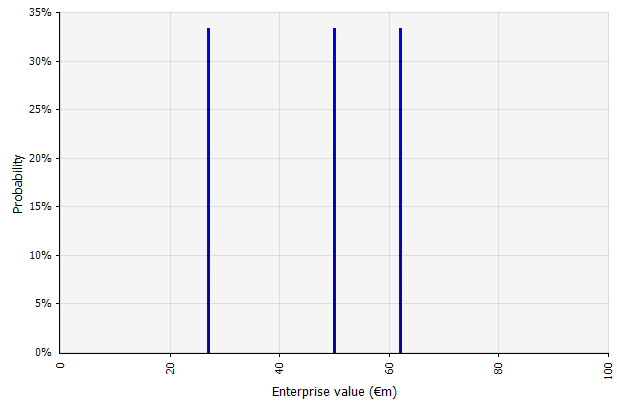以最簡單的形式，敏感性分析，這可以模擬例如銷售增長高於和低於基本情況 10% 的影響，使用固定、半可變和可變成本的給定組合來估計底線影響。 在更複雜的形式中，您從完全不同的角度考慮每種情況的未來，並分析不同的技術發展、競爭動態和宏觀趨勢對公司業績的影響。 通常情況下，不幸的是，這些場景的選擇非常隨意，有時還考慮到了期望的最終結果。	三種不同的情景產生三種不同的結果，在此假設可能性相同。 不考慮高和低情景之外的結果概率。
創建具有明確識別概率的基本、上行和下行案例。 也就是說，熊市和牛市的情況包含，例如，每條尾巴都有 25% 的概率，而公允價值估計代表中點。 從風險管理的角度來看，這樣做的一個有用的好處是對尾部風險的明確分析，即上行和下行情景之外的事件。	晨星估值手冊插圖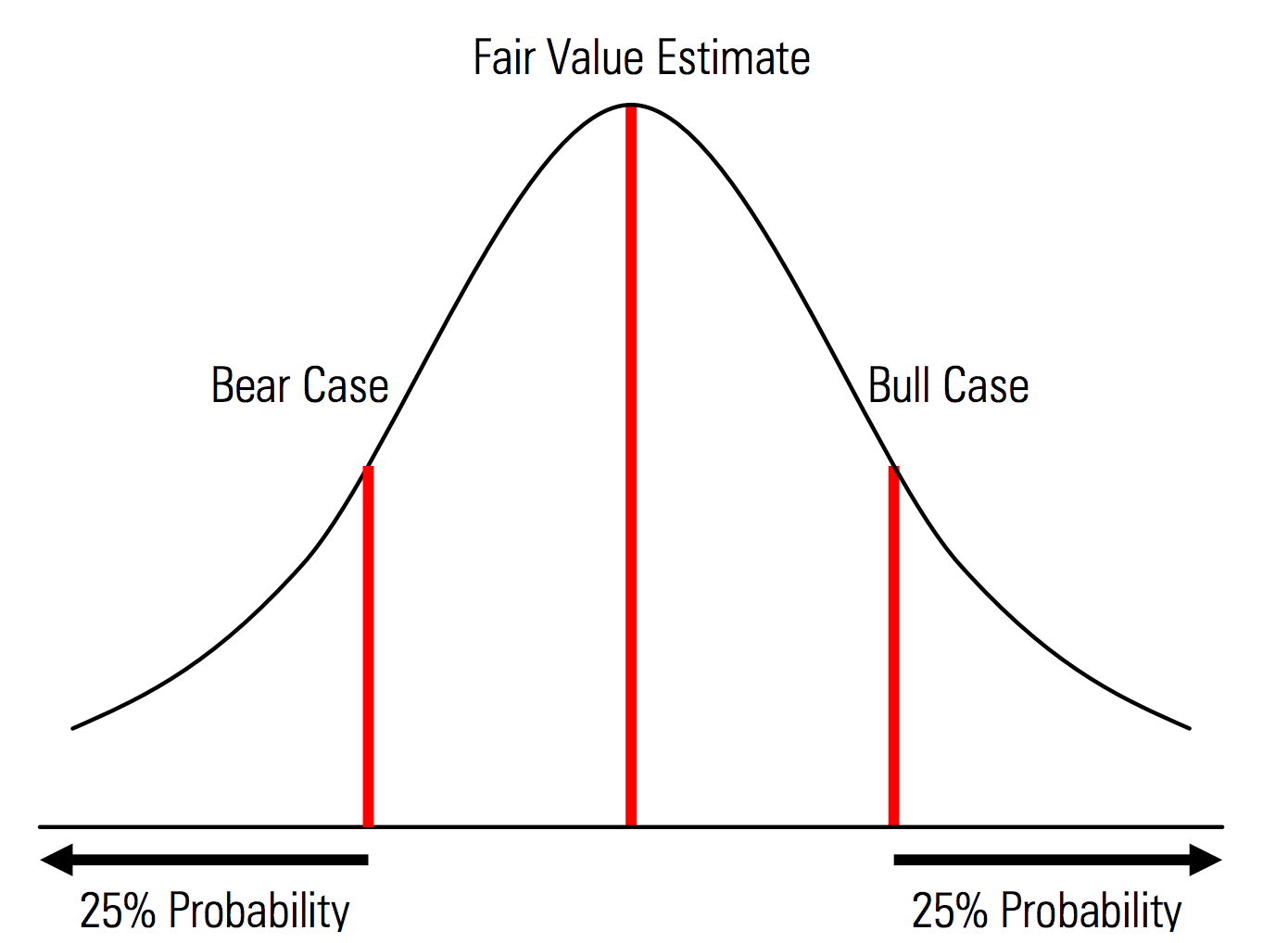
使用概率分佈和蒙特卡羅模擬。 使用概率分佈允許您對預測中的所有可能結果進行建模和可視化。 這不僅可以在總體層面上進行，還可以針對詳細的個人輸入、假設和驅動因素進行。 然後使用蒙特卡羅方法在總體水平上計算得到的概率分佈，從而分析幾個不確定變量如何影響整體結果的不確定性。 或許最重要的是，該方法迫使參與分析和決策的每個人明確認識到預測中固有的不確定性，並以概率進行思考。 正如其他方法一樣，這也有其缺點，包括使用更複雜的模型可能帶來的錯誤精度和過度自信的風險，以及選擇合適的概率分佈和估計它們的參數所需的額外工作，否則只能進行點估計用過的。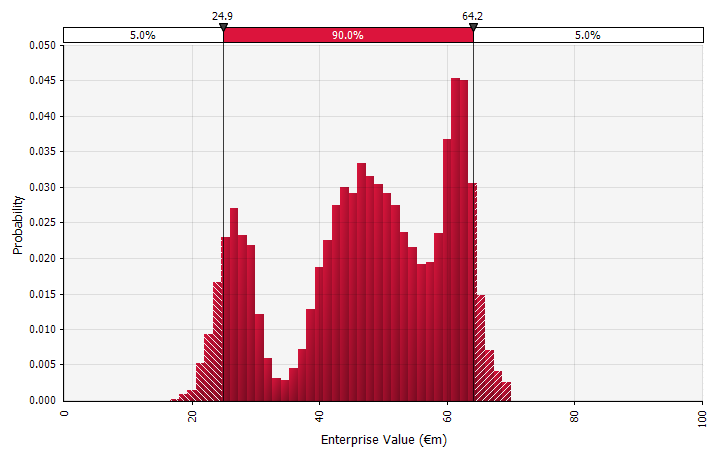

什麼是蒙特卡羅模擬？

蒙特卡洛模擬模擬財務預測和估計中不同結果的概率。 他們的名字來自摩納哥的蒙特卡洛地區，這里以高端賭場而聞名於世； 隨機結果是這項技術的核心，就像輪盤賭和老虎機一樣。 蒙特卡羅模擬在廣泛的領域非常有用，包括工程、項目管理、石油和天然氣勘探以及其他資本密集型行業、研發和保險； 在這裡，我專注於金融和商業領域的應用。

概率分佈

在模擬中，不確定性輸入使用概率分佈來描述，由均值和標準偏差等參數描述。 財務預測中的示例輸入可以是任何東西，從收入和利潤到更精細的東西，例如商品價格、擴張的資本支出或外匯匯率。

當一個或多個輸入被描述為概率分佈時，輸出也成為概率分佈。 計算機從每個輸入分佈中隨機抽取一個數字併計算並保存結果。 這會重複數百、數千或數万次，每次都稱為迭代。 綜合起來，這些迭代近似於最終結果的概率分佈。

輸入類型

輸入分佈可以是連續的，其中隨機生成的值可以取分佈下的任何值（例如正態分佈），也可以是離散的，其中概率附加到兩個或多個不同的場景。

模擬還可以包含不同類型的分佈的混合。 舉個例子，一個藥物研發項目有幾個階段，每個階段都有不同的成功或失敗概率。 這可以與描述每個階段所需的不確定投資金額和潛在收入的連續分佈相結合，如果項目產生的產品進入市場。 下圖顯示了這種模擬的輸出：損失 500 萬歐元到 5000 萬歐元（現值）的全部投資的概率約為 65%，淨收益的概率約為 35%。 100 到 250 歐元——如果 MIRR 或 NPV 等關鍵輸出指標顯示為點估計而不是概率分佈，則會丟失信息。

蒙特卡洛模擬實踐

蒙特卡洛模擬沒有得到更廣泛使用的一個原因是典型的財務日常工具不能很好地支持它們。 Excel 和 Google 表格在每個單元格中保存一個數字或公式結果，雖然它們可以定義概率分佈並生成隨機數，但從頭開始構建具有蒙特卡洛功能的財務模型很麻煩。 而且，雖然許多金融機構和投資公司使用蒙特卡羅模擬來評估衍生品、分析投資組合等，但他們的工具通常是內部開發的、專有的或過於昂貴——這使得個人金融專業人士無法使用它們。

因此，我想提請注意 Excel 插件，例如 Palisade 的 @RISK、Vose 的 ModelRisk 和 RiskAMP，它們極大地簡化了蒙特卡羅模擬的工作，並允許您將它們集成到現有模型中。 在以下演練中，我將使用@RISK。

案例研究：使用蒙特卡洛模擬進行現金流預測

讓我們回顧一個簡單的例子來說明蒙特卡洛模擬的關鍵概念：五年現金流預測。 在本演練中，我建立並填充了一個用於估值的基本現金流模型，逐漸用概率分佈替換輸入，最後運行模擬並分析結果。

步驟 1. 選擇或構建模型

首先，我使用一個簡單的模型，重點突出使用概率分佈的關鍵特徵。 請注意，首先，此模型與任何其他 Excel 模型沒有什麼不同； 我上面提到的插件適用於您現有的模型和電子表格。 下面的模型是一個簡單的現成版本，其中填充了形成一個場景的假設。

步驟 2. 創建第一個概率分佈

首先，我們需要收集做出假設所需的信息，然後我們需要選擇正確的概率分佈來插入。 重要的是要注意，無論您採用哪種方法來處理不確定性，關鍵輸入/假設的來源都是相同的。 商業盡職調查是在預計市場發展、行業趨勢和競爭動態的背景下對公司業務計劃的全面審查，通常包括從歷史數據中推斷、納入專家意見、進行市場研究和採訪市場參與者。 根據我的經驗，專家和市場參與者很樂意討論不同的情景、風險和結果範圍。 然而，大多數都沒有明確描述概率分佈。

現在讓我們從第一個預測年（2018 年）的估計銷售增長開始，逐個用概率分佈替換我們的關鍵輸入值。 可以通過 15 天的免費試用期評估用於 Excel 的 @RISK 插件，因此您可以從 Palisade 網站下載並單擊幾下進行安裝。 啟用@RISK 插件後，選擇您想要分佈的單元格，然後在菜單中選擇“定義分佈”。

然後，您從出現的分佈調色板中選擇一個。 @RISK 軟件提供了 70 多種不同的發行版可供選擇，因此一開始選擇其中一種可能會讓人不知所措。 以下是我最常使用的少數指南：

普通的。 由平均值和標準差定義。 由於其簡單性，這是一個很好的起點，並且適合作為晨星方法的擴展，您可以在其中定義一個分佈，該分佈可能涵蓋給定輸入的可能已經定義的場景或範圍，確保案例圍繞基本案例對稱，並且每條尾巴的概率看起來是合理的（比如晨星例子中的 25%）。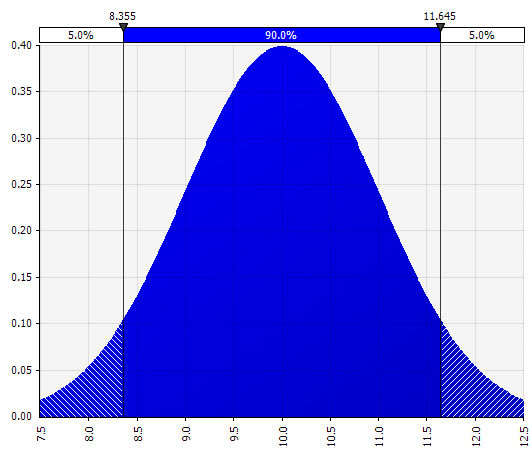
約翰遜時刻。 選擇此選項可讓您定義偏態分佈和尾部更粗或更細的分佈（技術上添加偏度和峰度參數）。 在幕後，這使用一種算法來選擇反映四個所選參數的四個分佈之一，但這對用戶是不可見的——我們只需要關注參數。 有時，在為輸入收集信息的過程中，很明顯正態分佈是不合適的。 例如，對於一家處於行業周期低谷或高峰的公司，未來五年（例如五年）業績好壞的概率是不對稱的。 越接近峰值，越有可能出現低迷而不是持續強勁的表現。 這是傾斜分佈可能有用的地方。 在許多金融領域，關於“肥尾”的概念已經寫了很多。 似乎正態分佈通常不能很好地描述實際結果，本應非常罕見的事件比正態分佈所顯示的更頻繁地發生。
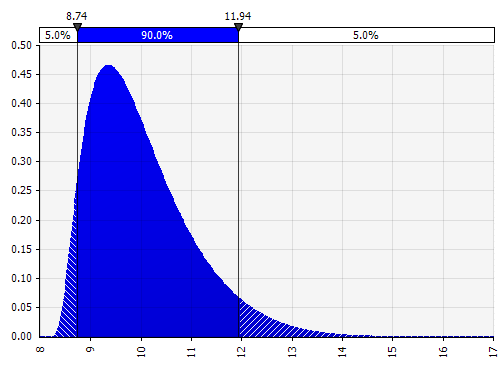離散的。 概率被賦予兩個或多個特定值。 回到開頭的分階段研發項目示例，每個階段的成功概率被建模為二元離散分佈，結果為 1 表示成功，0 表示失敗。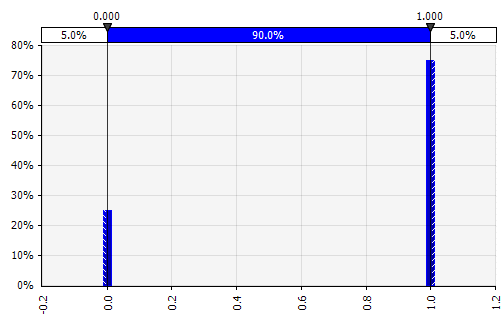
分佈擬合。 當您擁有大量歷史數據點時，分佈擬合功能很有用。 例如，這並不意味著三年或四年的歷史銷售增長，而是時間序列數據，例如商品價格、貨幣匯率或其他市場價格，其中歷史可以提供有關未來趨勢和不確定性程度的有用信息。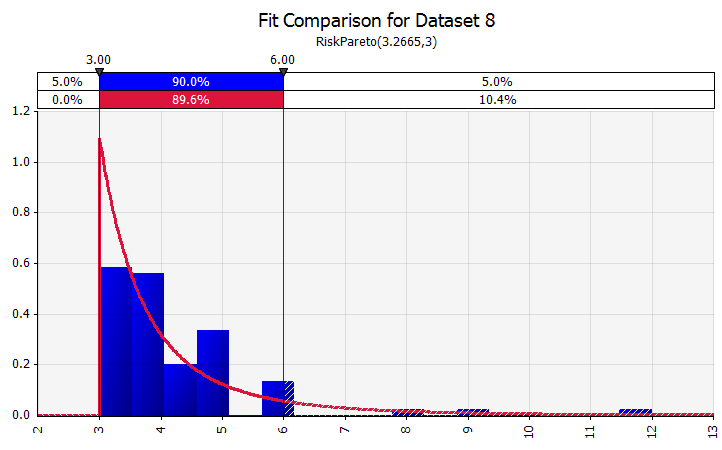
將幾種不同的分佈組合成一個。 為了減輕個人偏見的潛在影響，將不同來源的輸入納入假設和/或審查和討論結果通常是一個好主意。 有不同的方法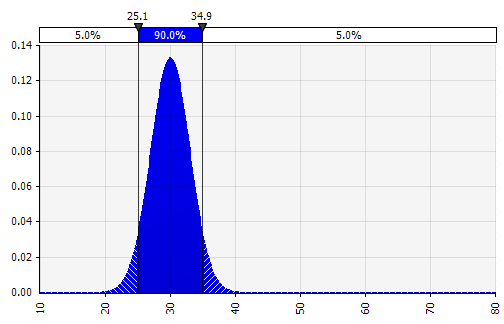： 準備草稿或初稿，然後與專家、更廣泛的管理團隊或其他決策者一起審查。 在會議中共同開發最重要的分佈。 這可以帶來良好的討論和更好的結果，但與往常一樣，小組的組成至關重要； 代表不同的觀點/職能並營造一種充滿活力但相互尊重的辯論氛圍當然是有幫助的。 為每個關鍵來源開發一個分佈，並將它們組合起來，根據你對每個來源的信任程度進行加權。 如果從幾位不同的專家那裡獲得意見，最好讓他們每個人都提供自己的觀點，獨立於其他人，然後合併為一個。 @RISK 函數 MakeRiskInput 為我們完成了這項工作。	重量：20% 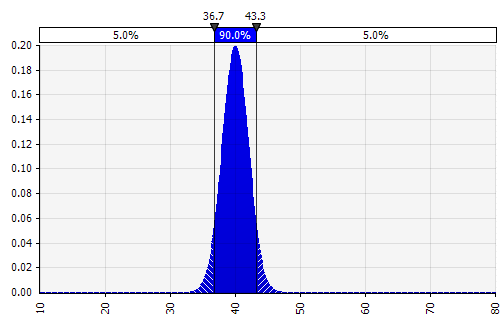+ 重量：20% 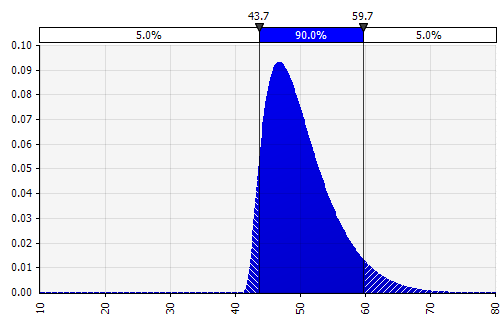+ 重量：60% =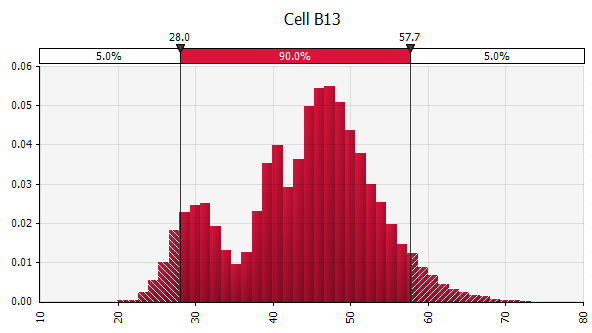
手繪。 為了在討論中快速說明一個分佈，或者如果您在起草一個不容易從現有調色板創建的模型時需要一個分佈，手繪功能很有用。 顧名思義，這允許您使用簡單的繪畫工具繪製分佈。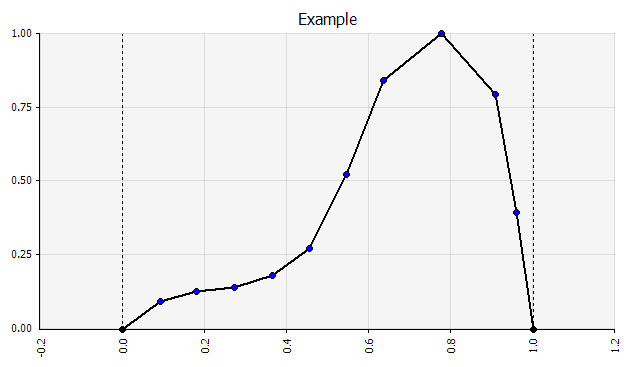

現在我們看到分佈的可視化，左側有一些參數。 平均值和標準差符號應該看起來很熟悉。 在正態分佈的情況下，平均值將是我們之前在單元格中輸入的單個值。 這里以 2018 年的銷售概率分佈為例，其中 10% 代表平均值。 雖然您的典型模型要么只關注 10% 的數字，要么有可能分別增長 15% 和 5% 的“牛市”和“熊市”情景，現在這提供了有關所有預期潛在結果的信息。

蒙特卡羅模擬的一個好處是低概率尾部結果可以引發思考和討論。 僅顯示上行和下行情景可能會引入決策者將其解釋為外部界限的風險，從而忽略任何外部情景。 這可能導致有缺陷的決策制定，並暴露於超出組織或個人對風險的承受能力的結果。 如果所討論的情況會產生災難性後果，即使是 5% 或 1% 的概率也可能是不可接受的。

步驟 3. 將收入預測從一年擴大到幾年

使用蒙特卡羅建模，請注意不確定性和概率分佈如何疊加，例如隨著時間的推移。 讓我們回顧一個例子。 由於每年的銷售額取決於前一年的增長，我們可以可視化並看到我們對 2022 年銷售額的估計比 2018 年的估計更不確定（使用每年的標準差和 95% 置信區間顯示）。 為簡單起見，以下示例指定了 2018 年一年的增長率，然後將相同的增長率應用於接下來的每一年，直到 2022 年。另一種方法是有五個獨立的分佈，每年一個。

第 4 步：繼續使用損益表——將利潤率表示為概率分佈

我們現在估計 2018 年 EBIT 利潤率的概率分佈（如下突出顯示），類似於我們為銷售增長所做的那樣。

在這裡，我們可以使用相關函數來模擬相對市場份額和盈利能力之間存在明顯相關性的情況，反映了規模經濟。 可以對具有較高銷售增長相對於市場和相應較高的相對市場份額的情景進行建模，以與較高的息稅前利潤率呈正相關。 在公司的財富與其他一些外部因素（例如油價或外匯匯率）密切相關的行業中，定義該因素的分佈並模擬與銷售和盈利能力的相關性是有意義的。

根據可用時間、交易規模和其他因素，建立運營模型並明確輸入最不確定的變量通常是有意義的。 其中包括：產品數量和價格、商品價格、外匯匯率、主要間接費用項目、每月活躍用戶和每單位平均收入 (ARPU)。 還可以對數量變量以外的變量進行建模，例如開發時間、上市時間或市場採用率。

步驟 5. 資產負債表和現金流量表

使用概述的方法，我們現在可以繼續查看資產負債表和現金流量表，填充假設並在有意義的地方使用概率分佈。

關於資本支出的說明：這可以以絕對金額或銷售額的百分比來建模，可能與更大的逐步投資相結合； 例如，製造設施可能有明確的產能限制和大量的擴張投資或當銷售額超過閾值時需要新設施。 由於說 1,000 或 10,000 次迭代中的每一次都將完全重新計算模型，因此可以使用一個簡單的公式來觸發投資成本（如果/當達到一定數量）。

第 6 步：完成模型

與標準財務模型相比，建立蒙特卡洛模型多了一個步驟：我們要評估結果的單元需要專門指定為輸出單元。 該軟件將保存這些單元的每次模擬迭代的結果，供我們在模擬完成後進行評估。 每次迭代都會重新計算整個模型中的所有單元格，但在其他未指定為輸入或輸出單元格的單元格中的迭代結果會丟失，並且在模擬完成後無法進行分析。 正如您在下面的屏幕截圖中所見，我們將 MIRR 結果單元格指定為輸出單元格。

完成模型構建後，只需按下“開始模擬”並等待幾秒鐘，即可首次運行模擬。

步驟 7. 解釋結果

以概率表示的輸出。 雖然我們的模型之前為修改後的 IRR 提供了一個單一值，但我們現在可以清楚地看到圍繞該值存在許多具有不同概率的潛在結果。 這使我們能夠改寫問題，例如“我們會通過這項投資達到我們的最低迴報率嗎？” “我們有多大可能達到或超過我們的障礙率？” 您可以使用例如置信區間來探索哪些結果最有可能。 在將結果傳達給不同的利益相關者時，可視化很有幫助，您可以覆蓋其他交易的輸出，以直觀地比較當前交易與其他交易的吸引力和（不確定性）（見下文）。

了解最終結果的不確定程度。 如果我們生成一個現金流隨時間變化的圖表，類似於我們最初為銷售所做的圖表，很明顯，即使在銷售和我們建模為概率分佈的其他輸入的不確定性相對較小的情況下，自由現金流的可變性也會變得顯著，結果從大約 50 萬歐元到 500 萬歐元不等——是 10 倍的係數——甚至與平均值只有一個標準差。 這是將不確定的假設疊加在一起的結果，這種影響在多年來“垂直”和“水平”向下貫穿財務報表。 可視化提供有關這兩種不確定性的信息。

敏感性分析：引入龍捲風圖。 另一個重要領域是了解哪些輸入對您的最終結果影響最大。 一個經典的例子是，相對於現金流預測，貼現率或終值假設的重要性通常被賦予太少的權重。 一種常見的處理方法是使用矩陣，在每個軸上放置一個鍵輸入，然後計算每個單元格中的結果（見下文）。 這在決策取決於一個或幾個關鍵假設的情況下尤其有用——在這些“你必須相信的”情況下，（例如）投資委員會或高級管理團隊的決策者可能對這些關鍵假設，以及上述矩陣等矩陣允許他們每個人找到與他們的觀點相對應的結果值，並可以據此決定、投票或提供建議。

使用蒙特卡洛模擬進行增強。 使用蒙特卡羅模擬時，該方法可以用另一種方​​法進行補充：龍捲風圖。 此可視化在垂直軸上列出了不同的不確定輸入和假設，然後顯示每個輸入和假設對最終結果的影響有多大。

這有多種用途，其中之一是它允許那些準備分析的人確保他們花費時間和精力來理解和驗證假設，這些假設大致對應於每個假設對最終結果的重要性。 It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein