Caja de herramientas del pronosticador: cómo realizar simulaciones de Monte Carlo

Resumen ejecutivo

Introducción

Primero, la única certeza es que no hay certeza. En segundo lugar, cada decisión como consecuencia es una cuestión de ponderación de probabilidades. Tercero, a pesar de la incertidumbre debemos decidir y debemos actuar. Y, por último, debemos juzgar las decisiones no solo por los resultados, sino también por cómo se tomaron esas decisiones. – Robert E. Rubín

Uno de los aspectos más importantes y desafiantes del pronóstico es manejar la incertidumbre inherente al examinar el futuro. Habiendo creado y poblado cientos de modelos financieros y operativos para LBO, recaudación de fondos de inicio, presupuestos, fusiones y adquisiciones y planes estratégicos corporativos desde 2003, he sido testigo de una amplia gama de enfoques para hacerlo. Cada CEO, CFO, miembro de la junta, inversionista o miembro del comité de inversión aporta su propia experiencia y enfoque a las proyecciones financieras y la incertidumbre, influenciado por diferentes incentivos. A menudo, comparar los resultados reales con las proyecciones proporciona una apreciación de cuán grandes pueden ser las desviaciones entre los pronósticos y los resultados reales y, por lo tanto, la necesidad de comprender y reconocer explícitamente la incertidumbre.

Inicialmente comencé usando análisis de sensibilidad y escenarios para modelar la incertidumbre, y aún los considero herramientas muy útiles. Desde que incorporé las simulaciones de Monte Carlo a mi caja de herramientas en 2010, descubrí que son una herramienta extremadamente efectiva para refinar y mejorar su forma de pensar sobre el riesgo y las probabilidades. He usado el enfoque para todo, desde la construcción de valoraciones de DCF, la valoración de opciones de compra en fusiones y adquisiciones y la discusión de riesgos con los prestamistas hasta la búsqueda de financiación y la orientación de la asignación de fondos de capital de riesgo para nuevas empresas. El enfoque siempre ha sido bien recibido por los miembros de la junta, los inversores y los equipos de alta dirección. En este artículo, proporciono un tutorial paso a paso sobre el uso de simulaciones de Monte Carlo en la práctica mediante la construcción de un modelo de valoración DCF.

Cada decisión es una cuestión de ponderación de probabilidades

Antes de comenzar con el estudio de caso, revisemos algunos enfoques diferentes para manejar la incertidumbre. El concepto de valor esperado, el promedio ponderado de probabilidad de los flujos de efectivo en todos los escenarios posibles, es Finanzas 101. Pero los profesionales de las finanzas y los tomadores de decisiones en general, adoptan enfoques muy diferentes al traducir esta idea simple en la práctica. El enfoque puede variar desde simplemente no reconocer o discutir la incertidumbre en absoluto, por un lado, hasta modelos y software sofisticados por el otro. En algunos casos, las personas pasan más tiempo discutiendo probabilidades que calculando flujos de efectivo.

Aparte de simplemente no abordarlo, examinemos algunas formas de manejar la incertidumbre en las proyecciones a mediano o largo plazo. Muchos de estos deben ser familiares para usted.

Creando un escenario. Este enfoque es el predeterminado para presupuestos, muchas nuevas empresas e incluso decisiones de inversión. Además de no contener información sobre el grado de incertidumbre o el reconocimiento de que los resultados pueden diferir de las proyecciones, puede ser ambiguo e interpretarse de manera diferente según la parte interesada. Algunos pueden interpretarlo como un objetivo ambicioso, donde es más probable que el resultado real se quede corto que superado. Algunos lo ven como un rendimiento de referencia con más ventajas que desventajas. Otros pueden verlo como un "caso base" con una probabilidad de 50/50 hacia arriba y hacia abajo. En algunos enfoques, especialmente para las nuevas empresas, es muy ambicioso y el fracaso o el déficit es el resultado más probable con diferencia, pero se utiliza una tasa de descuento más alta en un intento de tener en cuenta el riesgo.	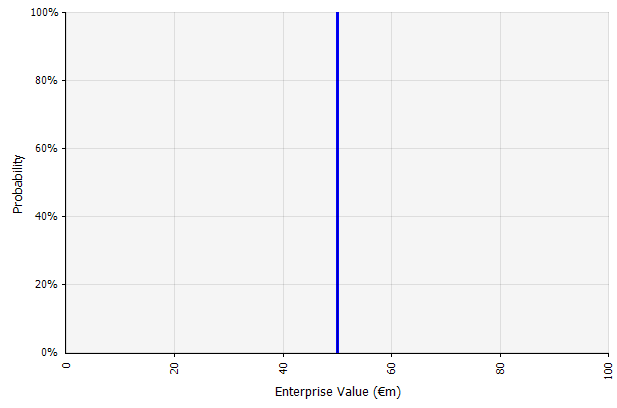Las entradas en la previsión de flujo de caja a largo plazo con este método son estimaciones puntuales, lo que arroja un resultado de estimación puntual de 50 millones de euros en este ejemplo, con una probabilidad implícita del 100 %.
Creación de múltiples escenarios. Este enfoque reconoce que es poco probable que la realidad se desarrolle de acuerdo con un único plan dado. 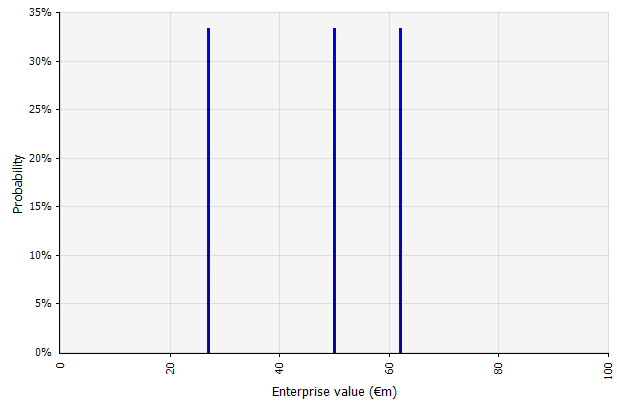En su forma más simple, el análisis de sensibilidad, esto podría simular el impacto de, por ejemplo, un crecimiento de las ventas del 10 % por encima y por debajo del caso base, utilizando una combinación dada de costos fijos, semivariables y variables para estimar el resultado final. impacto. En formas más complejas, piensa en el futuro desde una perspectiva completamente diferente para cada escenario y analiza el impacto que los diferentes desarrollos tecnológicos, dinámicas competitivas y macrotendencias tendrán en el desempeño de la empresa. A menudo, lamentablemente, los escenarios se eligen de manera bastante arbitraria y, a veces, con un resultado final deseado en mente.	Los tres escenarios diferentes arrojan tres resultados diferentes, aquí asumidos como igualmente probables. No se consideran las probabilidades de resultados fuera de los escenarios alto y bajo.
Creación de casos base, al alza y a la baja con probabilidades explícitamente reconocidas. Es decir, los casos bajista y alcista contienen, por ejemplo, una probabilidad del 25% en cada cruce, y la estimación del valor razonable representa el punto medio. Un beneficio útil de esto desde una perspectiva de gestión de riesgos es el análisis explícito del riesgo de cola, es decir, eventos fuera de los escenarios alcistas y bajistas.	Ilustración del Manual de valoración de Morningstar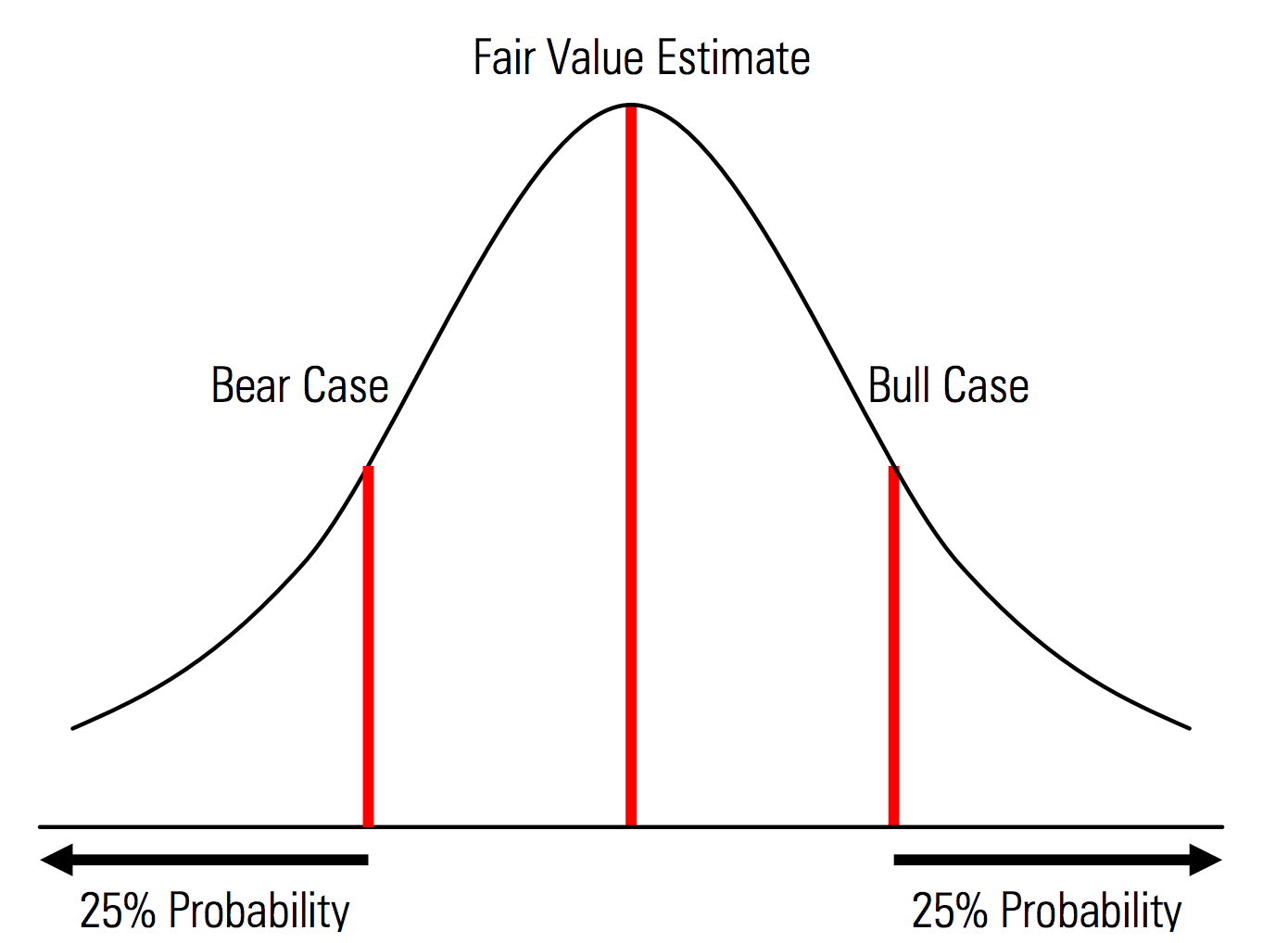
Uso de distribuciones de probabilidad y simulaciones de Monte Carlo. El uso de distribuciones de probabilidad le permite modelar y visualizar la gama completa de resultados posibles en el pronóstico. Esto se puede hacer no solo a nivel agregado, sino también para entradas, suposiciones e impulsores individuales detallados. Luego se utilizan métodos de Monte Carlo para calcular las distribuciones de probabilidad resultantes a nivel agregado, lo que permite el análisis de cómo varias variables inciertas contribuyen a la incertidumbre de los resultados generales. Quizás lo más importante es que el enfoque obliga a todos los involucrados en el análisis y la decisión a reconocer explícitamente la incertidumbre inherente a los pronósticos ya pensar en probabilidades. Al igual que los otros enfoques, esto tiene sus inconvenientes, incluido el riesgo de precisión falsa y el exceso de confianza resultante que puede surgir con el uso de un modelo más sofisticado, y el trabajo adicional requerido para seleccionar distribuciones de probabilidad adecuadas y estimar sus parámetros donde, de lo contrario, solo se necesitarían estimaciones puntuales. usado.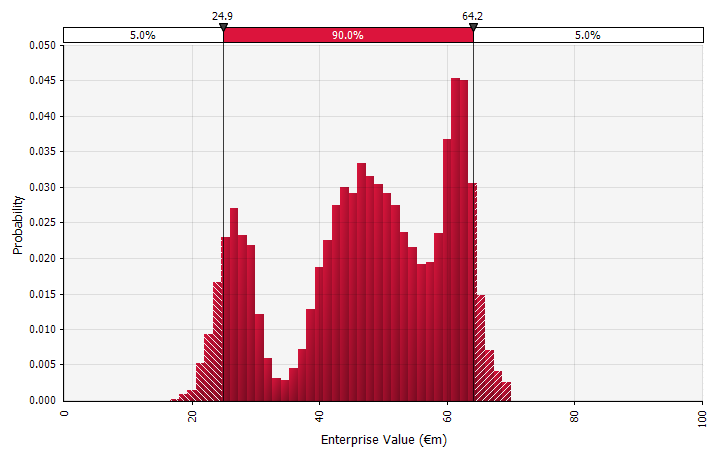

¿Qué es una simulación Monte Carlo?

Las simulaciones de Monte Carlo modelan la probabilidad de diferentes resultados en estimaciones y pronósticos financieros. Obtienen su nombre del área de Monte Carlo en Mónaco, que es mundialmente famosa por sus casinos de alta gama; los resultados aleatorios son fundamentales para la técnica, al igual que lo son para la ruleta y las máquinas tragamonedas. Las simulaciones de Monte Carlo son útiles en una amplia gama de campos, que incluyen ingeniería, gestión de proyectos, exploración de petróleo y gas y otras industrias intensivas en capital, investigación y desarrollo y seguros; aquí, me enfoco en aplicaciones en finanzas y negocios.

Distribuciones de probabilidad

En la simulación, las entradas inciertas se describen mediante distribuciones de probabilidad, descritas por parámetros como la media y la desviación estándar. Las entradas de ejemplo en las proyecciones financieras pueden ser cualquier cosa, desde ingresos y márgenes hasta algo más granular, como los precios de las materias primas, los gastos de capital para una expansión o las tasas de cambio de divisas.

Cuando una o más entradas se describen como distribuciones de probabilidad, la salida también se convierte en una distribución de probabilidad. Una computadora extrae aleatoriamente un número de cada distribución de entrada y calcula y guarda el resultado. Esto se repite cientos, miles o decenas de miles de veces, cada una de las cuales se denomina iteración. Cuando se toman en conjunto, estas iteraciones se aproximan a la distribución de probabilidad del resultado final.

Tipos de entradas

Las distribuciones de entrada pueden ser continuas , donde el valor generado aleatoriamente puede tomar cualquier valor bajo la distribución (por ejemplo, una distribución normal), o discretas , donde las probabilidades se asocian a dos o más escenarios distintos.

Una simulación también puede contener una mezcla de distribuciones de diferentes tipos. Tomemos, por ejemplo, un proyecto de I+D farmacéutico con varias etapas, cada una de las cuales tiene una probabilidad discreta de éxito o fracaso. Esto se puede combinar con distribuciones continuas que describen montos de inversión inciertos necesarios para cada etapa y los ingresos potenciales si el proyecto da como resultado un producto que llega al mercado. El siguiente gráfico muestra el resultado de una simulación de este tipo: una probabilidad de ~65 % de perder la inversión total de 5 millones de euros a 50 millones de euros (valor actual), y una probabilidad de ~35 % de una ganancia neta muy probablemente en el rango de De 100 € a 250 €: información que se perdería si las métricas de salida clave, como MIRR o NPV, se mostraran como estimaciones puntuales en lugar de distribuciones de probabilidad.

Simulaciones de Monte Carlo en la práctica

Una de las razones por las que las simulaciones de Monte Carlo no se usan más ampliamente es porque las herramientas financieras típicas del día a día no las admiten muy bien. Excel y Google Sheets contienen un resultado numérico o de fórmula en cada celda y, aunque pueden definir distribuciones de probabilidad y generar números aleatorios, crear un modelo financiero con la funcionalidad de Monte Carlo desde cero es engorroso. Y, aunque muchas instituciones financieras y empresas de inversión utilizan simulaciones de Monte Carlo para valorar derivados, analizar carteras y más, sus herramientas suelen desarrollarse internamente, son propietarias o tienen un costo prohibitivo, lo que las hace inaccesibles para el profesional financiero individual.

Por lo tanto, quiero llamar la atención sobre complementos de Excel como @RISK de Palisade, ModelRisk de Vose y RiskAMP, que simplifican enormemente el trabajo con simulaciones de Monte Carlo y le permiten integrarlas en sus modelos existentes. En el siguiente tutorial, usaré @RISK.

Estudio de caso: Proyecciones de flujo de caja con simulación Monte Carlo

Revisemos un ejemplo simple que ilustra los conceptos clave de una simulación de Monte Carlo: un pronóstico de flujo de efectivo de cinco años. En este tutorial, configuro y completo un modelo de flujo de efectivo básico para fines de valoración, reemplazo gradualmente las entradas con distribuciones de probabilidad y, finalmente, ejecuto la simulación y analizo los resultados.

Paso 1. Elegir o construir el modelo

Para comenzar, uso un modelo simple, centrado en resaltar las características clave del uso de distribuciones de probabilidad. Tenga en cuenta que, para empezar, este modelo no es diferente de cualquier otro modelo de Excel; los complementos que mencioné anteriormente funcionan con sus modelos y hojas de cálculo existentes. El siguiente modelo es una versión estándar simple poblada con suposiciones para formar un escenario.

Paso 2. Creando la Primera Distribución de Probabilidad

Primero, debemos recopilar la información necesaria para hacer nuestras suposiciones, luego debemos elegir las distribuciones de probabilidad correctas para insertar. Es importante tener en cuenta que la fuente de las entradas/suposiciones clave es la misma, independientemente del enfoque que adopte para manejar la incertidumbre. La diligencia debida comercial, una revisión integral del plan comercial de la empresa en el contexto del desarrollo del mercado proyectado, las tendencias de la industria y la dinámica competitiva, generalmente incluye la extrapolación de datos históricos, la incorporación de la opinión de expertos, la realización de estudios de mercado y entrevistas a los participantes del mercado. En mi experiencia, los expertos y los participantes del mercado están felices de discutir diferentes escenarios, riesgos y rangos de resultados. Sin embargo, la mayoría no describe explícitamente las distribuciones de probabilidad.

Ahora analicemos y reemplacemos nuestros valores de entrada clave con distribuciones de probabilidad uno por uno, comenzando con el crecimiento de ventas estimado para el primer año de pronóstico (2018). El complemento @RISK para Excel se puede evaluar con una prueba gratuita de 15 días para que pueda descargarlo del sitio web de Palisade e instalarlo con unos pocos clics. Con el complemento @RISK habilitado, seleccione la celda en la que desea la distribución y seleccione "Definir distribución" en el menú.

Luego selecciona uno de la paleta de distribuciones que aparece. El software @RISK ofrece más de 70 distribuciones diferentes para elegir, por lo que elegir una puede parecer abrumador al principio. A continuación hay una guía de algunos que uso con más frecuencia:

Normal. Definido por media y desviación estándar. Este es un buen punto de partida debido a su simplicidad, y adecuado como una extensión del enfoque de Morningstar, donde se define una distribución que cubre escenarios o rangos quizás ya definidos para una entrada dada, asegurando que los casos sean simétricos alrededor del caso base y que las probabilidades en cada cola parecen razonables (digamos 25% como en el ejemplo de Morningstar).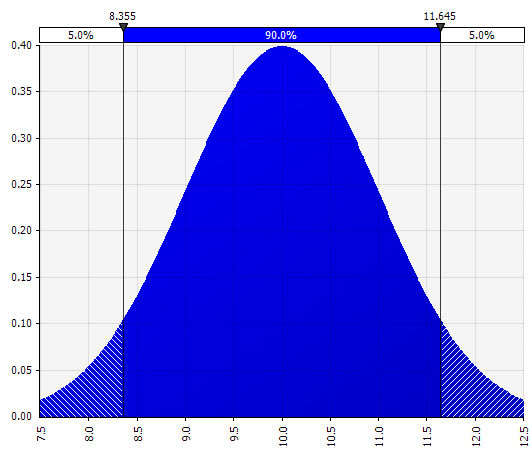
Momentos Johnson. Elegir esto le permite definir distribuciones sesgadas y distribuciones con colas más gruesas o más delgadas (técnicamente agregando parámetros de sesgo y curtosis). Detrás de escena, esto utiliza un algoritmo para elegir una de las cuatro distribuciones que refleja los cuatro parámetros elegidos, pero eso es invisible para el usuario; todo en lo que tenemos que concentrarnos son los parámetros. A veces, en el proceso de recopilación de información para la entrada, queda claro que la distribución normal no es adecuada. Por ejemplo, para una empresa en el punto más bajo o más alto de un ciclo industrial, las probabilidades de un mejor o peor desempeño en los próximos cinco años no serán simétricas. Cuanto más cerca del pico, más probable es que se produzca una recesión frente a un rendimiento sólido continuado. Aquí es donde una distribución sesgada puede ser útil. Mucho se ha escrito sobre el concepto de "colas gordas" en muchas áreas de las finanzas. Parece que la distribución normal a menudo no describe muy bien los resultados reales, con eventos que deberían ser muy raros ocurriendo con más frecuencia de lo que indicaría una distribución normal.
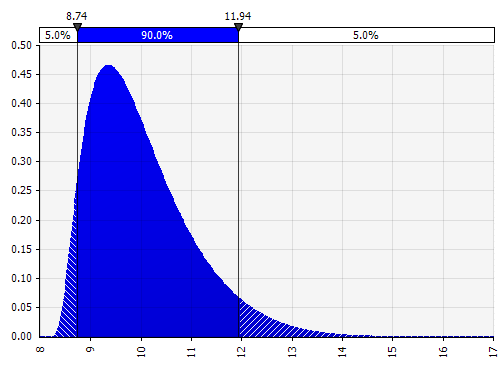Discreto. Donde se dan probabilidades a dos o más valores específicos. Volviendo al ejemplo del proyecto de I+D por etapas del principio, la probabilidad de éxito en cada etapa se modela como una distribución discreta binaria, con un resultado de 1 que representa el éxito y 0 el fracaso.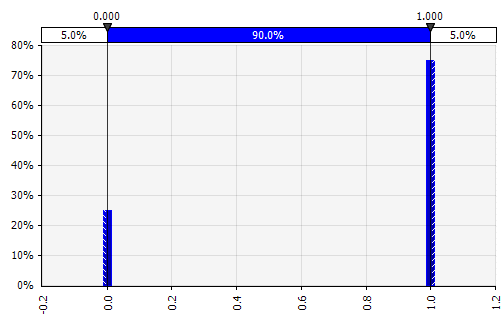
Montaje de distribución. Cuando tiene una gran cantidad de puntos de datos históricos, la funcionalidad de ajuste de distribución es útil. Esto no significa tres o cuatro años de crecimiento histórico de las ventas, por ejemplo, sino datos de series temporales como precios de materias primas, tipos de cambio de divisas u otros precios de mercado donde el historial puede brindar información útil sobre tendencias futuras y el grado de incertidumbre.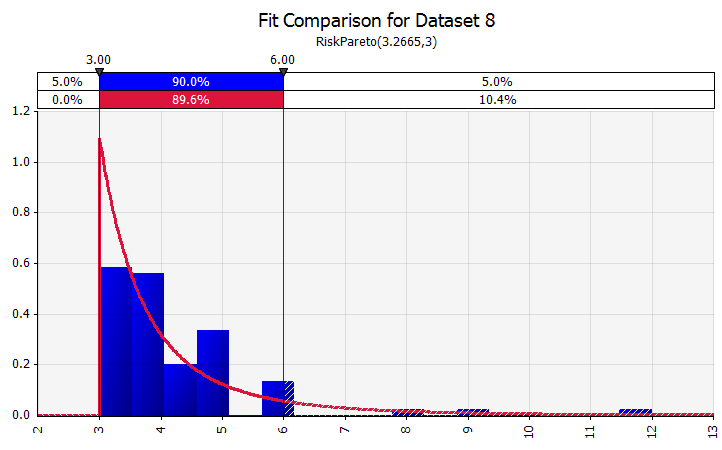
Combinar varias distribuciones diferentes en una sola. Para mitigar el impacto potencial de los sesgos individuales, a menudo es una buena idea incorporar los aportes de diferentes fuentes en una suposición y/o revisar y discutir los hallazgos. Hay diferentes enfoques: 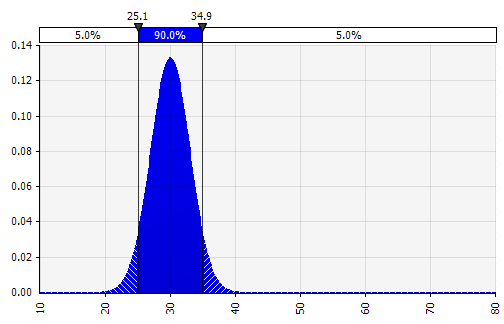Prepare un borrador o una primera vista y luego revíselo con expertos, el equipo de administración más amplio u otros tomadores de decisiones. Desarrollar las distribuciones más importantes de forma conjunta en una reunión. Esto puede conducir a una buena discusión y mejores resultados pero, como siempre, la composición del grupo es crítica; Por supuesto, es útil tener diferentes perspectivas/funciones representadas y fomentar una atmósfera de debate vigoroso pero respetuoso. Desarrolle una distribución para cada fuente clave y combínelas, ponderándolas según la fe que tenga en cada una. Si recibe aportes de varios expertos diferentes, puede ser una buena idea dejar que cada uno de ellos brinde su propio punto de vista, independientemente de los demás, y luego combinarlos en uno. La función @RISK MakeRiskInput hace esto por nosotros.	Peso: 20% 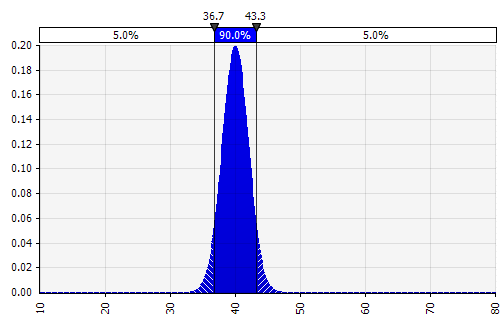+ Peso: 20% 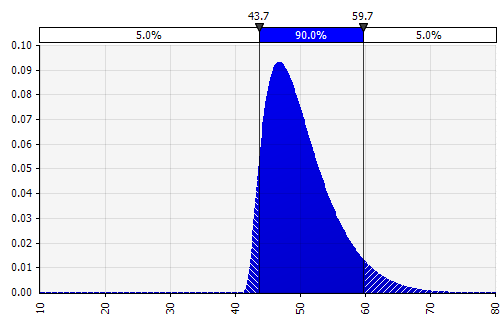+ Peso: 60% =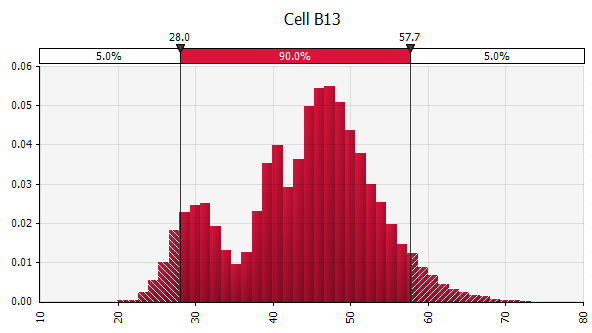
A mano. Para ilustrar rápidamente una distribución como parte de las discusiones o si necesita una distribución al dibujar un modelo que no se crea fácilmente a partir de la paleta existente, la funcionalidad de mano alzada es útil. Como su nombre lo indica, esto le permite dibujar la distribución utilizando una herramienta de pintura simple.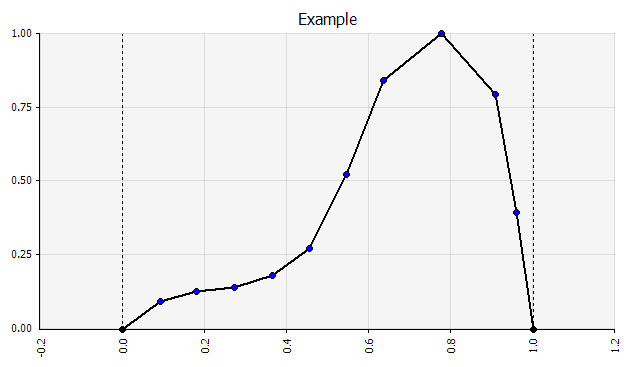

Ahora vemos una visualización de la distribución, con algunos parámetros en el lado izquierdo. Los símbolos de media y desviación estándar deberían resultarle familiares. En el caso de una distribución normal, la media sería lo que ingresamos previamente como un valor único en la celda. Aquí está la distribución de probabilidad de ventas de 2018 como ejemplo, con un 10 % que representa la media. Mientras que su modelo típico se centraría solo en la cifra del 10 % o tendría escenarios "alcistas" y "bajistas" con quizás un crecimiento del 15 % y 5 % respectivamente, esto ahora proporciona información sobre la gama completa de resultados potenciales esperados.

Un beneficio de las simulaciones de Monte Carlo es que los resultados finales de baja probabilidad pueden desencadenar el pensamiento y las discusiones. Solo mostrar escenarios al alza y a la baja puede introducir el riesgo de que los tomadores de decisiones los interpreten como los límites exteriores, descartando cualquier escenario que se encuentre fuera. Esto puede resultar en una toma de decisiones defectuosa, con exposición a resultados que se encuentran más allá de la tolerancia al riesgo de la organización o del individuo. Incluso una probabilidad del 5 % o del 1 % puede ser inaceptable si el escenario en cuestión tendría consecuencias catastróficas.

Paso 3. Ampliación de la previsión de ingresos de un año a varios

Con el modelo de Monte Carlo, tenga en cuenta cómo se superponen las distribuciones de probabilidad e incertidumbre, por ejemplo, a lo largo del tiempo. Repasemos un ejemplo. Dado que las ventas de cada año dependen del crecimiento de los anteriores, podemos visualizar y ver que nuestra estimación de las ventas de 2022 es más incierta que la de 2018 (que se muestra utilizando las desviaciones estándar y los intervalos de confianza del 95 % en cada año). En aras de la simplicidad, el siguiente ejemplo especifica el crecimiento de un año, 2018, y luego aplica esa misma tasa de crecimiento a cada uno de los años siguientes hasta 2022. Otro enfoque es tener cinco distribuciones independientes, una para cada año.

Paso 4. Continuación hacia abajo en el estado de resultados: expresión de los márgenes como distribuciones de probabilidad

Ahora estimamos una distribución de probabilidad para el margen EBIT en 2018 (resaltado a continuación) de manera similar a como lo hicimos para el crecimiento de las ventas.

Aquí, podemos utilizar la función de correlación para simular una situación en la que existe una clara correlación entre la cuota de mercado relativa y la rentabilidad, lo que refleja economías de escala. Los escenarios con un mayor crecimiento de las ventas en relación con el mercado y, en consecuencia, una mayor participación de mercado relativa pueden modelarse para tener una correlación positiva con márgenes EBIT más altos. En industrias donde la fortuna de una empresa está fuertemente correlacionada con algún otro factor externo, como los precios del petróleo o las tasas de cambio, puede tener sentido definir una distribución para ese factor y modelar una correlación con las ventas y la rentabilidad.

Según el tiempo disponible, el tamaño de la transacción y otros factores, a menudo tiene sentido construir un modelo operativo e ingresar explícitamente las variables más inciertas. Estos incluyen: volúmenes y precios de productos, precios de materias primas, tipos de cambio, gastos generales clave, usuarios activos mensuales e ingreso promedio por unidad (ARPU). También es posible modelar variables más allá de la cantidad, como el tiempo de desarrollo, el tiempo de comercialización o la tasa de adopción del mercado.

Paso 5. Balance General y Estado de Flujo de Efectivo

Usando el enfoque descrito, ahora podemos continuar con el balance general y el estado de flujo de efectivo, llenando con suposiciones y usando distribuciones de probabilidad donde tenga sentido.

Una nota sobre el gasto de capital: esto se puede modelar en cantidades absolutas o como un porcentaje de las ventas, potencialmente en combinación con inversiones escalonadas más grandes; una instalación de fabricación puede, por ejemplo, tener un límite de capacidad claro y una gran inversión de expansión o una nueva instalación necesaria cuando las ventas superan el umbral. Dado que cada una de las 1000 o 10 000 iteraciones será un recálculo completo del modelo, se puede usar una fórmula simple que activa el costo de inversión si/cuando se alcanza un cierto volumen.

Paso 6. Finalización del modelo

La construcción de un modelo de Monte Carlo tiene un paso adicional en comparación con un modelo financiero estándar: las celdas donde queremos evaluar los resultados deben designarse específicamente como celdas de salida. El software guardará los resultados de cada iteración de la simulación para esas celdas para que los evalúemos una vez finalizada la simulación. Todas las celdas del modelo completo se vuelven a calcular con cada iteración, pero los resultados de las iteraciones en otras celdas, que no están designadas como celdas de entrada o salida, se pierden y no se pueden analizar una vez que finaliza la simulación. Como puede ver en la captura de pantalla a continuación, designamos la celda de resultados MIRR para que sea una celda de salida.

Una vez que haya terminado de construir el modelo, es hora de ejecutar la simulación por primera vez simplemente presionando "iniciar simulación" y esperando unos segundos.

Paso 7. Interpretación de los resultados

Salidas expresadas como probabilidades. Mientras que nuestro modelo anteriormente nos daba un valor único para la TIR modificada, ahora podemos ver claramente que hay una serie de posibles resultados en torno a ese valor, con diferentes probabilidades. Esto nos permite reformular preguntas, como "¿Llegaremos a nuestra tasa de retorno mínima con esta inversión?" a "¿Cuán probable es que alcancemos o superemos nuestra tasa crítica?" Puede explorar qué resultados son más probables utilizando, por ejemplo, un intervalo de confianza. La visualización es útil cuando se comunican los resultados a las diferentes partes interesadas, y puede superponer los resultados de otras transacciones para comparar visualmente cuán atractiva e (in)segura es la actual en comparación con otras (ver a continuación).

Entender el grado de incertidumbre en el resultado final. Si generamos un gráfico de la variabilidad del flujo de efectivo a lo largo del tiempo, similar a lo que hicimos inicialmente para las ventas, queda claro que la variabilidad en el flujo de efectivo libre se vuelve significativa incluso con una incertidumbre relativamente modesta en las ventas y las otras entradas que modelamos como distribuciones de probabilidad. , con resultados que van desde alrededor de 0,5 millones de euros a 5,0 millones de euros, un factor de 10x, incluso solo una desviación estándar de la media. Este es el resultado de apilar supuestos inciertos uno encima del otro, un efecto que se combina tanto "verticalmente" a lo largo de los años como "horizontalmente" hacia abajo a lo largo de los estados financieros. Las visualizaciones proporcionan información sobre ambos tipos de incertidumbre.

Análisis de sensibilidad: Introducción al gráfico de tornado. Otra área importante es comprender qué entradas tienen el mayor impacto en su resultado final. Un ejemplo clásico es cómo la importancia de la tasa de descuento o los supuestos de valor terminal a menudo tienen muy poco peso en relación con la previsión del flujo de caja. Una forma común de manejar esto es mediante el uso de matrices en las que coloca una entrada clave en cada eje y luego calcula el resultado en cada celda (ver más abajo). Esto es útil especialmente en situaciones en las que las decisiones dependen de uno o unos pocos supuestos clave; en estas situaciones de "lo que hay que creer", los tomadores de decisiones en (por ejemplo) un comité de inversión o un equipo de alta dirección pueden tener diferentes puntos de vista de esos supuestos clave, y una matriz como la anterior permite que cada uno de ellos encuentre un valor de resultado correspondiente a su punto de vista, y puede decidir, votar o dar consejos en base a eso.

Mejora con simulaciones Monte Carlo. Al usar simulaciones de Monte Carlo, ese enfoque se puede complementar con otro: el diagrama de tornado. Esta visualización enumera las diferentes entradas y suposiciones inciertas en el eje vertical y luego muestra qué tan grande es el impacto de cada uno en el resultado final.

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein