مربع أدوات المتنبئ: كيفية أداء محاكاة مونت كارلو

ملخص تنفيذي

مقدمة

أولاً ، اليقين الوحيد هو أنه لا يوجد يقين. ثانيًا ، كل قرار نتيجة لذلك هو مسألة وزن الاحتمالات. ثالثًا ، على الرغم من عدم اليقين ، يجب أن نقرر ويجب أن نتصرف. وأخيرًا ، نحتاج إلى الحكم على القرارات ليس فقط بناءً على النتائج ، ولكن أيضًا على كيفية اتخاذ تلك القرارات. - روبرت إي. روبين

يعد التعامل مع عدم اليقين المتأصل في دراسة المستقبل أحد أهم جوانب التنبؤ وتحديًا. بعد أن قمت ببناء وتعبئة المئات من النماذج المالية والتشغيلية للمنظمات LBOs ، وجمع الأموال لبدء التشغيل ، والميزانيات ، وعمليات الدمج والاستحواذ ، والخطط الإستراتيجية للشركات منذ عام 2003 ، لقد شاهدت مجموعة واسعة من الأساليب للقيام بذلك. كل مدير تنفيذي أو مدير مالي أو عضو مجلس إدارة أو مستثمر أو عضو في لجنة الاستثمار يجلب معه خبرته الخاصة ومنهجيته في التعامل مع التوقعات المالية وعدم اليقين - متأثرًا بالحوافز المختلفة. في كثير من الأحيان ، توفر مقارنة النتائج الفعلية مقابل التوقعات تقديرًا لمدى اتساع الانحرافات بين التوقعات والنتائج الفعلية ، وبالتالي الحاجة إلى فهم عدم اليقين والاعتراف به صراحة.

بدأت في البداية باستخدام تحليلات السيناريو والحساسية لنمذجة عدم اليقين ، وما زلت أعتبرها أدوات مفيدة للغاية. منذ إضافة محاكاة مونت كارلو إلى صندوق أدواتي في عام 2010 ، وجدتها أداة فعالة للغاية لتحسين وتحسين طريقة تفكيرك في المخاطر والاحتمالات. لقد استخدمت النهج في كل شيء بدءًا من إنشاء تقييمات التدفقات النقدية المخصومة ، وتقييم خيارات الاتصال في عمليات الاندماج والاستحواذ ، ومناقشة المخاطر مع المقرضين إلى البحث عن التمويل وتوجيه تخصيص تمويل رأس المال الجريء للشركات الناشئة. لطالما حظي النهج بقبول جيد من قبل أعضاء مجلس الإدارة والمستثمرين وفرق الإدارة العليا. في هذه المقالة ، أقدم برنامجًا تعليميًا خطوة بخطوة حول استخدام محاكاة مونت كارلو عمليًا من خلال بناء نموذج تقييم DCF.

كل قرار هو مسألة وزن الاحتمالات

قبل البدء بدراسة الحالة ، دعنا نراجع بعض الأساليب المختلفة للتعامل مع عدم اليقين. مفهوم القيمة المتوقعة - المتوسط ​​المرجح للاحتمالية للتدفقات النقدية في جميع السيناريوهات الممكنة - هو التمويل 101. لكن المتخصصين الماليين وصناع القرار على نطاق أوسع ، يتخذون مناهج مختلفة للغاية عند ترجمة هذه الرؤية البسيطة إلى ممارسة. يمكن أن يتراوح النهج من عدم التعرف على عدم اليقين أو مناقشته على الإطلاق ، من ناحية ، إلى النماذج والبرامج المعقدة من ناحية أخرى. في بعض الحالات ، ينتهي الأمر بالناس إلى قضاء المزيد من الوقت في مناقشة الاحتمالات بدلاً من حساب التدفقات النقدية.

بصرف النظر عن عدم معالجته ببساطة ، دعنا ندرس بعض الطرق للتعامل مع عدم اليقين في التوقعات متوسطة أو طويلة الأجل. يجب أن يكون العديد من هؤلاء مألوفًا لك.

خلق سيناريو واحد. هذا النهج هو الإعداد الافتراضي للميزانيات والعديد من الشركات الناشئة وحتى قرارات الاستثمار. إلى جانب عدم احتوائه على أي معلومات حول درجة عدم اليقين أو الاعتراف بأن النتائج قد تختلف عن التوقعات ، يمكن أن تكون غامضة ويتم تفسيرها بشكل مختلف وفقًا لأصحاب المصلحة. قد يفسرها البعض على أنها هدف ممتد ، حيث من المرجح أن تكون النتيجة الفعلية أقل من تجاوزها. يراها البعض على أنها أداء أساسي مع وجود اتجاه صعودي أكثر من الجانب السلبي. قد يراها الآخرون على أنها "حالة أساسية" مع احتمال 50/50 لأعلى ولأسفل. في بعض المناهج ، خاصة بالنسبة للشركات الناشئة ، يكون الأمر طموحًا للغاية والفشل أو النقص هو النتيجة الأكثر ترجيحًا إلى حد بعيد ، ولكن يتم استخدام معدل خصم أعلى في محاولة لحساب المخاطر.	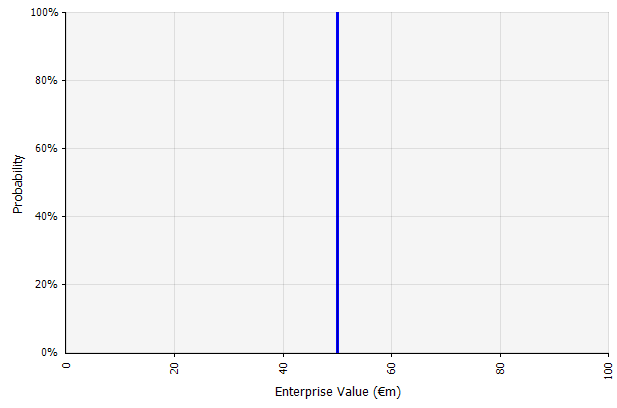تعتبر المدخلات في توقعات التدفقات النقدية طويلة الأجل بموجب هذا النهج كلها تقديرات نقطية ، مما يؤدي إلى نتيجة تقدير نقطية قدرها 50 مليون يورو في هذا المثال ، مع احتمال ضمني بنسبة 100٪.
إنشاء سيناريوهات متعددة. يدرك هذا النهج أنه من غير المرجح أن تتكشف الحقيقة وفقًا لخطة واحدة معينة. 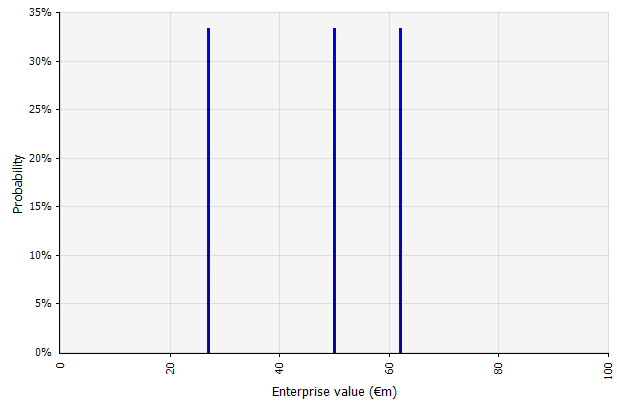في أبسط أشكاله ، تحليل الحساسية ، يمكن أن يحاكي هذا تأثير ، على سبيل المثال ، نمو المبيعات بنسبة 10٪ أعلى وأدنى من الحالة الأساسية ، باستخدام مزيج معين من التكاليف الثابتة وشبه المتغيرة والمتغيرة لتقدير المحصلة النهائية تأثير. في الأشكال الأكثر تعقيدًا ، تفكر في المستقبل من منظور مختلف تمامًا لكل سيناريو ، وتحلل تأثير التطورات التكنولوجية المختلفة والديناميكيات التنافسية والاتجاهات الكلية على أداء الشركة. في كثير من الأحيان ، يتم اختيار السيناريوهات للأسف بشكل تعسفي تمامًا ، وفي بعض الأحيان مع وضع النتيجة النهائية المرغوبة في الاعتبار.	تسفر السيناريوهات الثلاثة المختلفة عن ثلاث نتائج مختلفة ، يُفترض هنا أن تكون متساوية في الاحتمال. لا تؤخذ في الاعتبار احتمالات النتائج خارج السيناريوهات المرتفعة والمنخفضة.
إنشاء حالات أساسية ، وحالات عكسية ، وسلبية مع الاعتراف صراحةً بالاحتمالات. أي أن حالات الدببة والثور تحتوي ، على سبيل المثال ، على احتمال 25٪ في كل ذيل ، ويمثل تقدير القيمة العادلة نقطة الوسط. من الفوائد المفيدة لهذا من منظور إدارة المخاطر التحليل الصريح للمخاطر الخلفية ، أي الأحداث خارج سيناريوهات الاتجاه الصعودي والتراجع.	رسم توضيحي من دليل التقييم Morningstar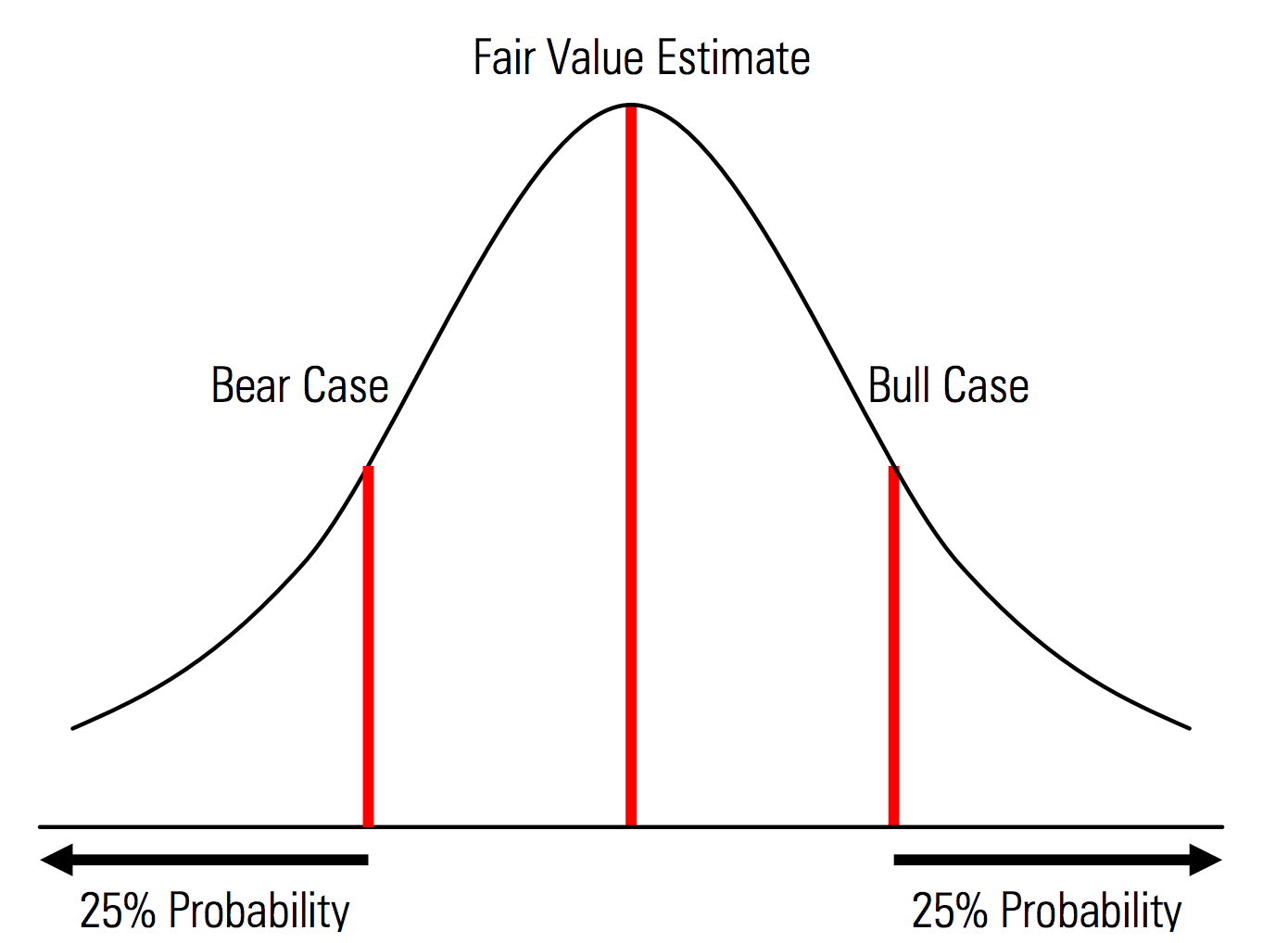
استخدام التوزيعات الاحتمالية ومحاكاة مونت كارلو. يتيح لك استخدام التوزيعات الاحتمالية تصميم وتصور النطاق الكامل للنتائج المحتملة في التنبؤ. يمكن القيام بذلك ليس فقط على المستوى الكلي ، ولكن أيضًا من أجل المدخلات والافتراضات والدوافع الفردية المفصلة. تُستخدم بعد ذلك طرق مونت كارلو لحساب التوزيعات الاحتمالية الناتجة على المستوى الكلي ، مما يسمح بتحليل كيفية مساهمة العديد من المتغيرات غير المؤكدة في عدم اليقين في النتائج الإجمالية. ولعل الأهم من ذلك ، أن النهج يجبر جميع المشاركين في التحليل والقرار على الاعتراف صراحةً بعدم اليقين المتأصل في التنبؤ ، والتفكير في الاحتمالات. تمامًا مثل الأساليب الأخرى ، فإن هذا له عيوبه ، بما في ذلك مخاطر الدقة الزائفة وما ينتج عنه من ثقة مفرطة قد تأتي مع استخدام نموذج أكثر تعقيدًا ، والعمل الإضافي المطلوب لاختيار توزيعات احتمالية مناسبة وتقدير معلماتها حيث تكون تقديرات النقطة فقط بخلاف ذلك. تستخدم.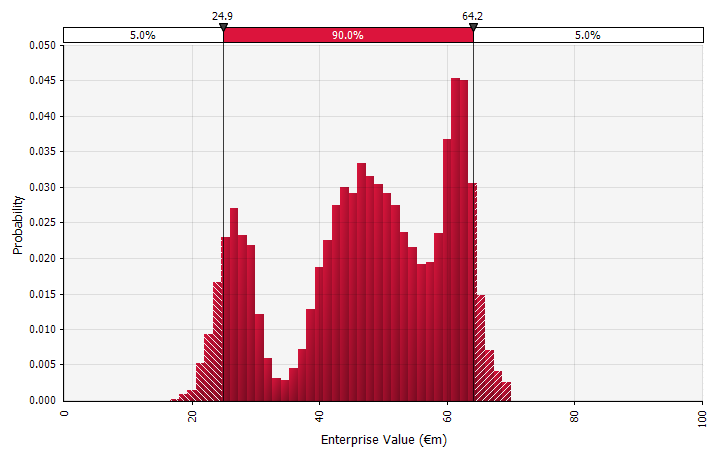

ما هي محاكاة مونت كارلو؟

نماذج محاكاة مونت كارلو نموذج احتمالية النتائج المختلفة في التنبؤات والتقديرات المالية. اكتسبوا اسمهم من منطقة مونت كارلو في موناكو ، المشهورة عالميًا بكازينوهاتها الراقية ؛ تعتبر النتائج العشوائية أساسية في هذه التقنية ، تمامًا مثل لعبة الروليت وآلات القمار. تعد محاكاة مونت كارلو مفيدة في مجموعة واسعة من المجالات ، بما في ذلك الهندسة وإدارة المشاريع واستكشاف النفط والغاز وغيرها من الصناعات كثيفة رأس المال والبحث والتطوير والتأمين ؛ هنا ، أركز على التطبيقات في التمويل والأعمال.

التوزيعات الاحتمالية

في المحاكاة ، يتم وصف المدخلات غير المؤكدة باستخدام التوزيعات الاحتمالية ، الموصوفة بواسطة معلمات مثل الانحراف المتوسط ​​والمعياري. يمكن أن تكون المدخلات النموذجية في الإسقاطات المالية أي شيء من الإيرادات والهوامش إلى شيء أكثر دقة ، مثل أسعار السلع أو النفقات الرأسمالية للتوسع أو أسعار الصرف الأجنبي.

عندما يتم وصف واحد أو أكثر من المدخلات كتوزيعات احتمالية ، يصبح الناتج أيضًا توزيعًا احتماليًا. يرسم الكمبيوتر رقمًا عشوائيًا من كل توزيع إدخال ويحسب النتيجة ويحفظها. يتكرر هذا مئات أو آلاف أو عشرات الآلاف من المرات ، كل منها يسمى التكرار. عند أخذها معًا ، تقارب هذه التكرارات التوزيع الاحتمالي للنتيجة النهائية.

أنواع المدخلات

يمكن أن تكون توزيعات الإدخال إما مستمرة ، حيث يمكن أن تأخذ القيمة المولدة عشوائيًا أي قيمة تحت التوزيع (على سبيل المثال التوزيع الطبيعي) ، أو منفصلة ، حيث ترتبط الاحتمالات بسيناريوهين مميزين أو أكثر.

يمكن أن تحتوي المحاكاة أيضًا على مزيج من التوزيعات من أنواع مختلفة. خذ ، على سبيل المثال ، مشروع بحث وتطوير صيدلاني من عدة مراحل لكل منها احتمال منفصل للنجاح أو الفشل. يمكن دمج هذا مع التوزيعات المستمرة التي تصف مبالغ الاستثمار غير المؤكدة اللازمة لكل مرحلة والإيرادات المحتملة إذا كان المشروع ينتج منتجًا يصل إلى السوق. يوضح الرسم البياني أدناه الناتج من مثل هذه المحاكاة: احتمالية بنسبة 65٪ تقريبًا خسارة الاستثمار بالكامل من 5 مليون يورو إلى 50 مليون يورو (القيمة الحالية) ، واحتمال ~ 35٪ لصافي الربح على الأرجح في نطاق € 100 إلى € 250 - المعلومات التي سيتم فقدها إذا تم عرض مقاييس المخرجات الرئيسية مثل MIRR أو NPV كتقديرات نقطية بدلاً من توزيعات احتمالية.

محاكاة مونت كارلو في الممارسة

أحد أسباب عدم استخدام محاكاة مونت كارلو على نطاق واسع هو أن أدوات التمويل اليومية النموذجية لا تدعمها جيدًا. يحتوي كل من Excel و Google Sheets على رقم واحد أو نتيجة صيغة واحدة في كل خلية ، وعلى الرغم من أنه يمكنهم تحديد توزيعات الاحتمالية وإنشاء أرقام عشوائية ، إلا أن إنشاء نموذج مالي بوظيفة Monte Carlo من البداية أمر مرهق. وعلى الرغم من أن العديد من المؤسسات المالية وشركات الاستثمار تستخدم محاكاة مونت كارلو لتقييم المشتقات وتحليل المحافظ وغير ذلك ، فإن أدواتها يتم تطويرها عادةً داخليًا أو مملوكة أو باهظة الثمن - مما يجعلها غير قابلة للوصول إلى متخصص التمويل الفردي.

وبالتالي ، أود أن ألفت الانتباه إلى مكونات Excel الإضافية مثلRISK by Palisade و ModelRisk by Vose و RiskAMP ، والتي تبسط إلى حد كبير العمل مع محاكاة مونت كارلو وتسمح لك بدمجها في نماذجك الحالية. في الإرشادات التالية ، سأستخدمRISK.

دراسة حالة: توقعات التدفق النقدي مع محاكاة مونت كارلو

دعونا نراجع مثالًا بسيطًا يوضح المفاهيم الأساسية لمحاكاة مونت كارلو: توقعات التدفق النقدي لمدة خمس سنوات. في هذه الإرشادات التفصيلية ، قمت بإعداد نموذج التدفق النقدي الأساسي وملؤه لأغراض التقييم ، واستبدل المدخلات بالتوزيعات الاحتمالية تدريجيًا ، وأخيرًا تشغيل المحاكاة وتحليل النتائج.

الخطوة 1. اختيار أو بناء النموذج

للبدء ، أستخدم نموذجًا بسيطًا يركز على إبراز الميزات الرئيسية لاستخدام التوزيعات الاحتمالية. لاحظ أنه لبدء التشغيل ، لا يختلف هذا النموذج عن أي نموذج Excel آخر ؛ تعمل المكونات الإضافية التي ذكرتها أعلاه مع النماذج وجداول البيانات الموجودة لديك. النموذج أدناه هو نسخة بسيطة جاهزة للاستخدام مع افتراضات لتشكيل سيناريو واحد.

الخطوة 2. إنشاء التوزيع الاحتمالي الأول

أولاً ، نحتاج إلى جمع المعلومات اللازمة لعمل افتراضاتنا ، ثم نحتاج إلى اختيار التوزيعات الاحتمالية الصحيحة لإدراجها. من المهم ملاحظة أن مصدر المدخلات / الافتراضات الرئيسية هو نفسه بغض النظر عن النهج الذي تتبعه للتعامل مع عدم اليقين. تشمل العناية التجارية الواجبة ، وهي مراجعة شاملة لخطة عمل الشركة في سياق تطوير السوق المتوقع ، واتجاهات الصناعة ، والديناميكيات التنافسية ، استقراءً من البيانات التاريخية ، ودمج آراء الخبراء ، وإجراء أبحاث السوق ، وإجراء مقابلات مع المشاركين في السوق. من واقع خبرتي ، يسعد الخبراء والمشاركين في السوق بمناقشة السيناريوهات والمخاطر ونطاقات النتائج المختلفة. ومع ذلك ، فإن معظمهم لا يصف التوزيعات الاحتمالية صراحة.

دعنا الآن نتصفح ونستبدل قيم المدخلات الرئيسية لدينا بتوزيعات احتمالية واحدة تلو الأخرى ، بدءًا من نمو المبيعات المقدّر للسنة المتوقعة الأولى (2018). يمكن تقييم المكون الإضافيRISK لبرنامج Excel من خلال إصدار تجريبي مجاني مدته 15 يومًا حتى تتمكن من تنزيله من موقع Palisade على الويب وتثبيته ببضع نقرات. مع تمكين المكون الإضافيRISK ، حدد الخلية التي تريد التوزيع فيها وحدد "تحديد التوزيع" في القائمة.

ثم تختار واحدًا من لوحة التوزيعات التي تظهر. يقدم برنامجRISK أكثر من 70 توزيعًا مختلفًا للاختيار من بينها ، لذا قد يبدو اختيار أحدها أمرًا صعبًا في البداية. يوجد أدناه دليل لحفنة أستخدمها في أغلب الأحيان:

طبيعي. معرّفة بالمتوسط ​​والانحراف المعياري. هذه نقطة انطلاق جيدة بسبب بساطتها ، ومناسبة كامتداد لنهج Morningstar ، حيث يمكنك تحديد توزيع يغطي ربما سيناريوهات أو نطاقات محددة بالفعل لمدخل معين ، مما يضمن أن الحالات متماثلة حول الحالة الأساسية و أن الاحتمالات في كل ذيل تبدو معقولة (لنقل 25٪ كما في مثال Morningstar).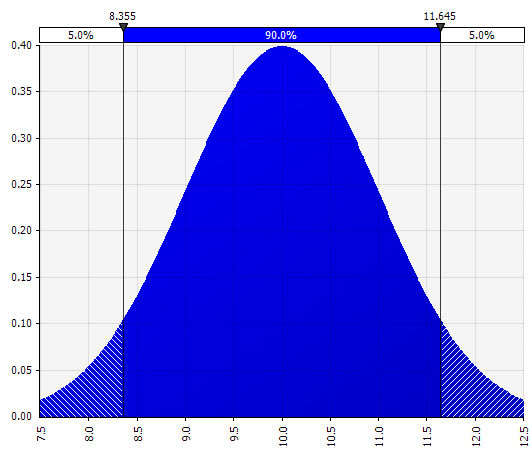
لحظات جونسون. يتيح لك اختيار هذا تحديد توزيعات منحرفة وتوزيعات ذات ذيول أسمن أو أرق (إضافة معلمات الانحراف والتفرطح تقنيًا). وراء الكواليس ، يستخدم هذا خوارزمية لاختيار واحد من أربعة توزيعات تعكس المعلمات الأربعة المختارة ، ولكن هذا غير مرئي للمستخدم - كل ما علينا التركيز عليه هو المعلمات. في بعض الأحيان ، أثناء عملية جمع المعلومات للمدخلات ، يتضح أن التوزيع الطبيعي غير مناسب. على سبيل المثال ، بالنسبة لشركة في أدنى مستوى أو ذروة دورة صناعية ، فإن احتمالات الأداء الأفضل أو الأسوأ خلال السنوات الخمس التالية ، على سبيل المثال ، لن تكون متماثلة. كلما اقتربنا من الذروة ، زاد احتمال حدوث تراجع مقابل استمرار الأداء القوي. هذا هو المكان الذي يمكن أن يكون فيه التوزيع المنحرف مفيدًا. لقد كتب الكثير عن مفهوم "ذيول السمين" في العديد من مجالات التمويل. يبدو أن التوزيع الطبيعي في كثير من الأحيان لا يصف النتائج الفعلية بشكل جيد للغاية ، مع الأحداث التي يجب أن تكون نادرة جدًا تحدث بشكل متكرر أكثر مما يشير إليه التوزيع الطبيعي.
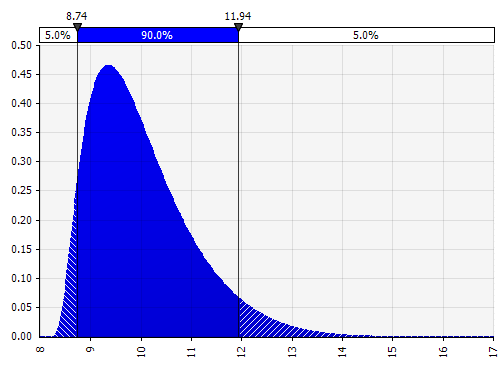منفصله. حيث يتم إعطاء الاحتمالات لقيمتين محددتين أو أكثر. بالعودة إلى مثال مشروع البحث والتطوير المرحلي في البداية ، فإن احتمالية النجاح في كل مرحلة على غرار التوزيع الثنائي المنفصل ، مع نتيجة 1 تمثل النجاح وصفر الفشل.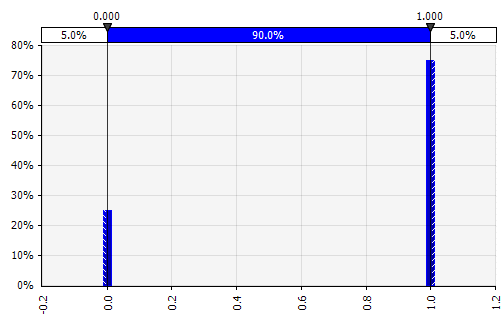
تركيب التوزيع. عندما يكون لديك عدد كبير من نقاط البيانات التاريخية ، تكون وظيفة ملاءمة التوزيع مفيدة. هذا لا يعني ثلاث أو أربع سنوات من النمو التاريخي للمبيعات ، على سبيل المثال ، ولكن بيانات السلاسل الزمنية مثل أسعار السلع أو أسعار صرف العملات أو أسعار السوق الأخرى حيث يمكن للتاريخ أن يقدم معلومات مفيدة حول الاتجاهات المستقبلية ودرجة عدم اليقين.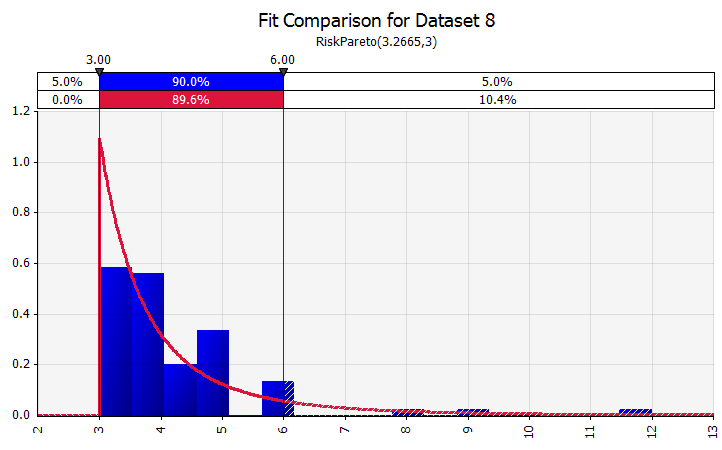
الجمع بين عدة توزيعات مختلفة في واحد. للتخفيف من التأثير المحتمل للتحيزات الفردية ، غالبًا ما يكون من الجيد دمج مدخلات المصادر المختلفة في الافتراض ، و / أو مراجعة النتائج ومناقشتها. هناك طرق مختلفة: قم بإعداد مسودة أو عرض أولي ثم قم بمراجعتها مع الخبراء أو فريق الإدارة الأوسع أو صانعي القرار الآخرين. وضع أهم التوزيعات بشكل مشترك في الاجتماع. هذا يمكن أن يؤدي إلى مناقشة جيدة ونتائج أفضل ولكن كما هو الحال دائما تكوين المجموعة أمر بالغ الأهمية ؛ من المفيد بالطبع وجود وجهات نظر / وظائف مختلفة وتعزيز جو من النقاش النشط والمحترم. طوِّر توزيعة واحدة لكل مصدر رئيسي ، واجمعها ، مُرجحة وفقًا لمقدار إيمانك بكل مصدر. إذا تم الحصول على مدخلات من عدة خبراء مختلفين ، فقد يكون من الجيد السماح لكل منهم بتقديم وجهة نظره الخاصة ، بشكل مستقل عن الآخرين ، ثم بعد ذلك يتم دمجه في واحد. تقوم وظيفةRISK MakeRiskInput بهذا نيابة عنا.	الوزن: 20٪ 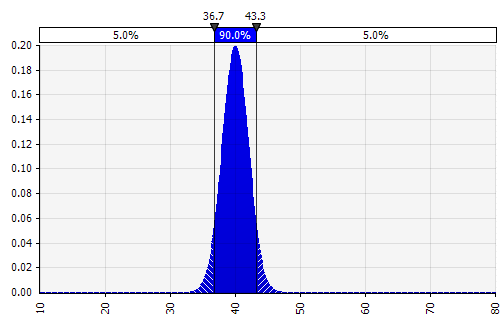+ الوزن: 20٪ 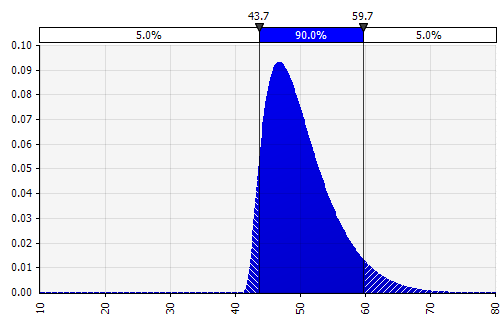+ الوزن: 60٪ =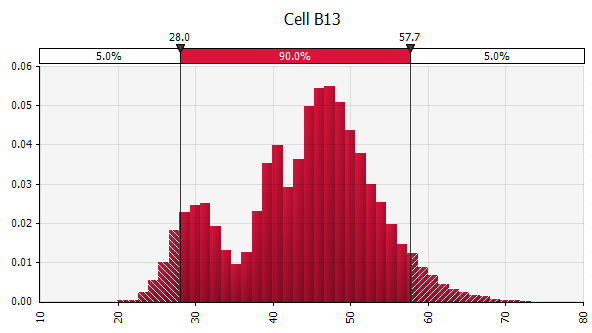
الحرية. لتوضيح التوزيع بسرعة كجزء من المناقشات أو إذا كنت بحاجة إلى توزيع عند صياغة نموذج لم يتم إنشاؤه بسهولة من اللوحة الحالية ، فإن الوظيفة اليدوية مفيدة. كما يوحي الاسم ، يتيح لك ذلك رسم التوزيع باستخدام أداة طلاء بسيطة.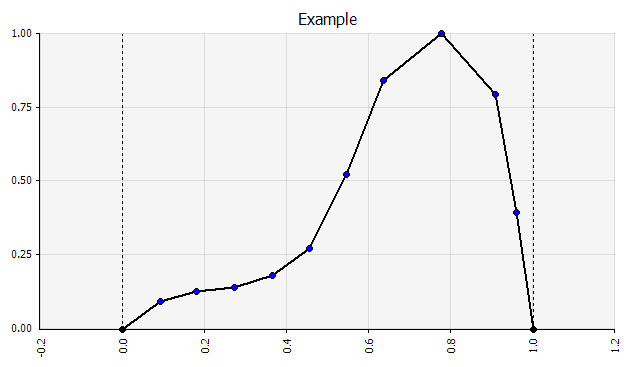

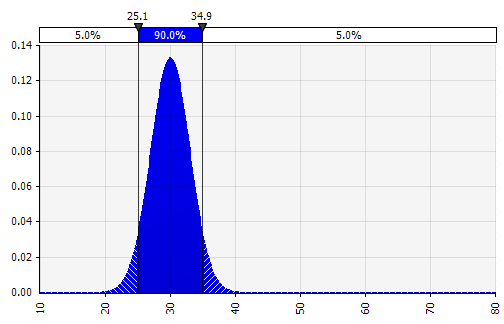
الآن نرى تصورًا للتوزيع ، مع بعض المعلمات على الجانب الأيسر. يجب أن تبدو رموز الانحراف المعياري والمتوسط ​​مألوفة. في حالة التوزيع الطبيعي ، سيكون المتوسط ​​هو ما أدخلناه سابقًا كقيمة واحدة في الخلية. فيما يلي توزيع احتمالية المبيعات لعام 2018 كمثال ، حيث يمثل 10٪ المتوسط. في حين أن نموذجك النموذجي إما سيركز فقط على رقم 10٪ ، أو لديه سيناريوهات "ثور" و "دب" مع نمو ربما بنسبة 15٪ و 5٪ على التوالي ، فإن هذا يوفر الآن معلومات حول النطاق الكامل للنتائج المحتملة المتوقعة.

تتمثل إحدى مزايا محاكاة مونت كارلو في أن النتائج ذات الاحتمالية المنخفضة يمكن أن تؤدي إلى التفكير والمناقشات. فقط عرض سيناريوهات الاتجاه الصعودي والهبوط يمكن أن يعرض المخاطر التي يفسرها صانعو القرار على أنها حدود خارجية ، مع استبعاد أي سيناريوهات تقع في الخارج. يمكن أن يؤدي هذا إلى اتخاذ قرارات معيبة ، مع التعرض لنتائج تتجاوز قدرة المؤسسة أو الفرد على تحمل المخاطر. حتى احتمال 5٪ أو 1٪ قد يكون غير مقبول إذا كان السيناريو المعني سيكون له عواقب وخيمة.

الخطوة 3. توسيع توقعات الإيرادات من سنة إلى عدة سنوات

مع نمذجة مونت كارلو ، ضع في اعتبارك كيف تتراكم توزيعات عدم اليقين والاحتمالية فوق بعضها البعض ، على سبيل المثال بمرور الوقت. دعنا نراجع مثالا. نظرًا لأن المبيعات في كل عام تعتمد على النمو في السنوات السابقة ، يمكننا أن نتصور ونرى أن تقديرنا لمبيعات 2022 غير مؤكد أكثر من تقديرنا لعام 2018 (يظهر باستخدام الانحرافات المعيارية وفواصل الثقة 95٪ في كل عام). من أجل التبسيط ، يحدد المثال أدناه النمو لسنة واحدة ، 2018 ، ثم يطبق معدل النمو نفسه على كل من السنوات التالية حتى عام 2022. وهناك نهج آخر يتمثل في الحصول على خمسة توزيعات مستقلة ، واحدة لكل عام.

الخطوة 4. الاستمرار في بيان الدخل - معبراً عن الهوامش كتوزيعات احتمالية

نحن نقدر الآن التوزيع الاحتمالي لهامش الأرباح قبل الفوائد والضرائب في عام 2018 (الموضح أدناه) بشكل مشابه للطريقة التي فعلناها من أجل نمو المبيعات.

هنا ، يمكننا استخدام دالة الارتباط لمحاكاة موقف يوجد فيه ارتباط واضح بين حصة السوق النسبية والربحية ، مما يعكس اقتصاديات الحجم. يمكن نمذجة السيناريوهات ذات النمو المرتفع للمبيعات مقارنة بالسوق وحصة السوق النسبية المرتفعة بحيث يكون لها ارتباط إيجابي بهوامش أرباح قبل احتساب الفوائد والضرائب أعلى. في الصناعات التي ترتبط فيها ثروة الشركة ارتباطًا وثيقًا ببعض العوامل الخارجية الأخرى ، مثل أسعار النفط أو أسعار الصرف الأجنبي ، يمكن أن يكون تحديد توزيع لهذا العامل ونمذجة الارتباط مع المبيعات والربحية أمرًا منطقيًا.

اعتمادًا على الوقت المتاح وحجم المعاملة وعوامل أخرى ، غالبًا ما يكون من المنطقي بناء نموذج تشغيلي وإدخال المتغيرات الأكثر غموضًا بشكل صريح. وتشمل هذه: أحجام المنتجات وأسعارها ، وأسعار السلع ، وأسعار الصرف الأجنبي ، والبنود العامة الرئيسية ، والمستخدمون النشطون شهريًا ، ومتوسط ​​الإيرادات لكل وحدة (ARPU). من الممكن أيضًا وضع نماذج تتجاوز متغيرات المقدار مثل وقت التطوير أو وقت الوصول إلى السوق أو معدل تبني السوق.

الخطوة 5. الميزانية العمومية وبيان التدفقات النقدية

باستخدام النهج الموضح ، يمكننا الآن المتابعة من خلال الميزانية العمومية وبيان التدفقات النقدية ، وملء الافتراضات واستخدام التوزيعات الاحتمالية حيث يكون ذلك منطقيًا.

ملاحظة حول النفقات الرأسمالية: يمكن نمذجة ذلك إما بالمبالغ المطلقة أو كنسبة مئوية من المبيعات ، وربما بالاقتران مع الاستثمارات التدريجية الأكبر ؛ قد يكون لمنشأة التصنيع على سبيل المثال حد قدرة واضح واستثمار توسعي كبير أو منشأة جديدة ضرورية عندما تتجاوز المبيعات الحد الأدنى. نظرًا لأن كل تكرار على سبيل المثال 1،000 أو 10،000 سيكون إعادة حساب كاملة للنموذج ، يمكن استخدام صيغة بسيطة تؤدي إلى تكلفة الاستثمار إذا / عند الوصول إلى حجم معين.

الخطوة 6. الانتهاء من النموذج

يشتمل بناء نموذج مونت كارلو على خطوة إضافية واحدة مقارنة بالنموذج المالي القياسي: الخلايا التي نريد تقييم النتائج فيها تحتاج إلى تحديدها على وجه التحديد كخلايا مخرجات. سيحفظ البرنامج نتائج كل تكرار للمحاكاة لتلك الخلايا لنا لتقييمها بعد انتهاء المحاكاة. يتم إعادة حساب جميع الخلايا في النموذج بأكمله مع كل تكرار ، ولكن يتم فقد نتائج التكرارات في الخلايا الأخرى ، والتي لم يتم تحديدها كخلايا إدخال أو إخراج ، ولا يمكن تحليلها بعد انتهاء المحاكاة. كما ترى في لقطة الشاشة أدناه ، قمنا بتعيين خلية نتيجة MIRR لتكون خلية إخراج.

بمجرد الانتهاء من بناء النموذج ، حان الوقت لتشغيل المحاكاة لأول مرة عن طريق الضغط ببساطة على "بدء المحاكاة" والانتظار لبضع ثوان.

الخطوة 7. تفسير النتائج

يتم التعبير عن النواتج على أنها احتمالات. بينما أعطانا نموذجنا سابقًا قيمة واحدة لـ IRR المعدل ، يمكننا الآن أن نرى بوضوح أن هناك عددًا من النتائج المحتملة حول هذه القيمة ، مع احتمالات مختلفة. يتيح لنا ذلك إعادة صياغة الأسئلة ، مثل "هل سنواجه عقبة في معدل العائد مع هذا الاستثمار؟" إلى "ما مدى احتمالية إصابة أو تجاوز معدل عقبة لدينا؟" يمكنك استكشاف النتائج التي من المرجح أن تستخدم ، على سبيل المثال ، فترة الثقة. يكون التصور مفيدًا عند توصيل النتائج إلى مختلف أصحاب المصلحة ، ويمكنك تراكب المخرجات من المعاملات الأخرى لمقارنة بصريًا مدى جاذبية و (غير مؤكد) مقارنة بالآخرين (انظر أدناه).

فهم درجة عدم اليقين في النتيجة النهائية. إذا أنشأنا مخططًا لتقلبات التدفق النقدي بمرور الوقت ، على غرار ما فعلناه في البداية للمبيعات ، يصبح من الواضح أن التباين في التدفق النقدي الحر يصبح كبيرًا حتى مع عدم اليقين المتواضع نسبيًا في المبيعات والمدخلات الأخرى التي قمنا بنمذجة كتوزيعات احتمالية ، مع نتائج تتراوح من حوالي 0.5 مليون يورو إلى 5.0 مليون يورو - وهو عامل 10x - حتى انحراف معياري واحد فقط عن المتوسط. هذا هو نتيجة تكديس الافتراضات غير المؤكدة فوق بعضها البعض ، وهو تأثير يتراكم "عموديًا" على مر السنين ، و "أفقيًا" من خلال البيانات المالية. توفر التصورات معلومات حول كلا النوعين من عدم اليقين.

تحليل الحساسية: تقديم الرسم البياني للإعصار. مجال مهم آخر هو فهم المدخلات التي لها أكبر تأثير على النتيجة النهائية. المثال الكلاسيكي هو كيف يتم إعطاء أهمية سعر الخصم أو افتراضات القيمة النهائية في كثير من الأحيان القليل من الأهمية بالنسبة للتنبؤ بالتدفق النقدي. تتمثل إحدى الطرق الشائعة للتعامل مع هذا في استخدام المصفوفات حيث تقوم بوضع إدخال مفتاح واحد على كل محور ثم حساب النتيجة في كل خلية (انظر أدناه). هذا مفيد بشكل خاص في المواقف التي تعتمد فيها القرارات على واحد أو بضعة افتراضات رئيسية - في مواقف "ما يجب أن تصدقه" ، قد يكون لدى صانعي القرار (على سبيل المثال) في لجنة الاستثمار أو فريق الإدارة العليا وجهات نظر مختلفة حول هذه الافتراضات الرئيسية ، والمصفوفة مثل تلك أعلاه تسمح لكل واحد منهم بالعثور على قيمة نتيجة تتوافق مع وجهة نظرهم ، ويمكنهم أن يقرروا أو يصوتوا أو يقدموا المشورة بناءً على ذلك.

تعزيز محاكاة مونت كارلو. عند استخدام محاكاة مونت كارلو ، يمكن استكمال هذا النهج بآخر: مخطط الإعصار. يسرد هذا التصور المدخلات والافتراضات غير المؤكدة المختلفة على المحور الرأسي ثم يوضح مدى تأثير كل منها على النتيجة النهائية.

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein