Tahmincinin Araç Kutusu: Monte Carlo Simülasyonları Nasıl Gerçekleştirilir

Yönetici Özeti

Tanıtım

Birincisi, kesin olan tek şey, kesinliğin olmadığıdır. İkincisi, sonuç olarak her karar, olasılıkların tartılması meselesidir. Üçüncüsü, belirsizliğe rağmen karar vermeli ve harekete geçmeliyiz. Ve son olarak, kararları sadece sonuçlara göre değil, bu kararların nasıl verildiğine göre de değerlendirmemiz gerekiyor. – Robert E. Rubin

Tahminin en önemli ve zorlu yönlerinden biri, geleceği incelemenin doğasında var olan belirsizliği ele almaktır. 2003'ten bu yana LBO'lar, başlangıç ​​fonları, bütçeler, M&A ve kurumsal stratejik planlar için yüzlerce finansal ve işletme modeli oluşturup doldurduktan sonra, bunu yapmak için çok çeşitli yaklaşımlara tanık oldum. Her CEO, CFO, yönetim kurulu üyesi, yatırımcı veya yatırım komitesi üyesi, farklı teşviklerden etkilenen finansal tahminlere ve belirsizliğe kendi deneyimlerini ve yaklaşımlarını getirir. Çoğu zaman, gerçek sonuçları tahminlerle karşılaştırmak, tahminler ve gerçek sonuçlar arasındaki sapmaların ne kadar büyük olabileceğine ve dolayısıyla belirsizliği anlama ve açıkça tanıma ihtiyacına ilişkin bir değerlendirme sağlar.

Başlangıçta belirsizliği modellemek için senaryo ve duyarlılık analizlerini kullanmaya başladım ve hala onları çok faydalı araçlar olarak görüyorum. 2010'da araç kutuma Monte Carlo simülasyonları eklediğimden beri, bunların risk ve olasılıklar hakkında nasıl düşündüğünüzü iyileştirmek ve geliştirmek için son derece etkili bir araç olduğunu gördüm. DCF değerlemeleri oluşturmaktan, M&A'daki çağrı seçeneklerine değer vermekten ve kredi verenlerle riskleri tartışmaktan finansman aramaya ve yeni başlayanlar için VC finansmanı tahsisine rehberlik etmeye kadar her şey için bu yaklaşımı kullandım. Yaklaşım, yönetim kurulu üyeleri, yatırımcılar ve üst düzey yönetim ekipleri tarafından her zaman iyi karşılanmıştır. Bu makalede, bir DCF değerleme modeli oluşturarak Monte Carlo simülasyonlarını pratikte kullanma konusunda adım adım bir eğitim sunuyorum.

Her Karar Olasılıkların Tartılması Sorunudur

Örnek olay incelemesine başlamadan önce, belirsizliği ele almak için birkaç farklı yaklaşımı gözden geçirelim. Beklenen değer kavramı—tüm olası senaryolarda nakit akışlarının olasılık ağırlıklı ortalaması—Finans 101'dir. Ancak finans uzmanları ve daha geniş anlamda karar vericiler, bu basit kavrayışı uygulamaya dönüştürürken çok farklı yaklaşımlar benimserler. Yaklaşım, bir yanda belirsizliği hiç tanımamaktan ya da tartışmaktan, diğer yanda karmaşık modeller ve yazılımlara kadar değişebilir. Bazı durumlarda, insanlar nakit akışlarını hesaplamaktansa olasılıkları tartışmak için daha fazla zaman harcarlar.

Bunu basitçe ele almamanın yanı sıra, orta veya uzun vadeli tahminlerde belirsizliği ele almanın birkaç yolunu inceleyelim. Bunların birçoğu size tanıdık gelmelidir.

Tek bir senaryo oluşturmak. Bu yaklaşım, bütçeler, birçok girişim ve hatta yatırım kararları için varsayılandır. Belirsizliğin derecesi veya sonuçların tahminlerden farklı olabileceğinin kabulü hakkında herhangi bir bilgi içermemesinin yanı sıra, belirsiz olabilir ve paydaşa göre farklı yorumlanabilir. Bazıları bunu, gerçek sonucun aşmaktan ziyade eksik kalma olasılığının yüksek olduğu bir esneme hedefi olarak yorumlayabilir. Bazıları bunu, olumsuzdan çok olumlu yönleri olan temel bir performans olarak görüyor. Diğerleri bunu 50/50 olasılıkla yukarı ve aşağı bir "Temel Durum" olarak görebilir. Bazı yaklaşımlarda, özellikle yeni başlayanlar için, çok hırslıdır ve başarısızlık veya eksiklik açık ara daha muhtemel sonuçtur, ancak riski hesaba katmak için daha yüksek bir iskonto oranı kullanılır.	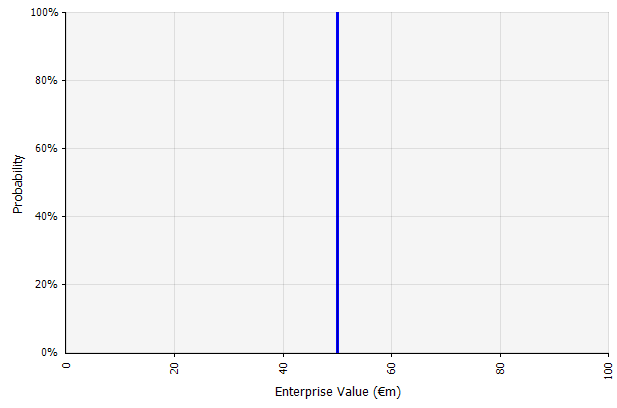Bu yaklaşım kapsamındaki uzun vadeli nakit akışı tahminindeki girdilerin tümü nokta tahminlerdir ve bu örnekte %100'lük örtük olasılıkla 50 milyon €'luk bir nokta tahmin sonucu verir.
Birden fazla senaryo oluşturma. Bu yaklaşım, gerçekliğin tek bir plana göre ortaya çıkma olasılığının olmadığını kabul eder. 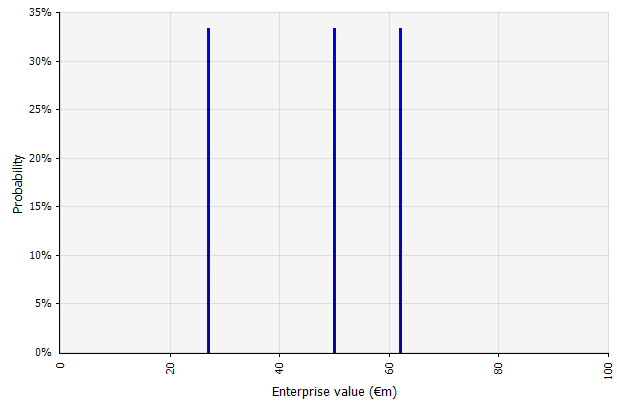En basit şekliyle, duyarlılık analizi, bu, örneğin, alt satırı tahmin etmek için belirli bir sabit, yarı değişken ve değişken maliyet karışımını kullanarak, temel durumun %10 üzerinde ve altındaki satış büyümesinin etkisini simüle edebilir. etki. Daha karmaşık formlarda, her senaryo için geleceği tamamen farklı bir perspektiften düşünür ve farklı teknolojik gelişmelerin, rekabet dinamiklerinin ve makro eğilimlerin şirketin performansı üzerindeki etkisini analiz edersiniz. Çoğu zaman, senaryolar ne yazık ki oldukça keyfi olarak ve bazen de istenen bir sonuç göz önünde bulundurularak seçilir.	Üç farklı senaryo, burada eşit derecede olası olduğu varsayılan üç farklı sonuç verir. Yüksek ve düşük senaryoların dışındaki sonuçların olasılıkları dikkate alınmaz.
Açıkça tanınan olasılıklarla taban, yukarı ve aşağı durumlar oluşturma. Yani, ayı ve boğa vakaları, örneğin her kuyrukta %25'lik bir olasılık içerir ve gerçeğe uygun değer tahmini orta noktayı temsil eder. Bunun bir risk yönetimi perspektifinden faydalı bir yararı, kuyruk riskinin, yani yukarı ve aşağı senaryoların dışındaki olayların açık analizidir.	Morningstar Değerleme El Kitabından Çizim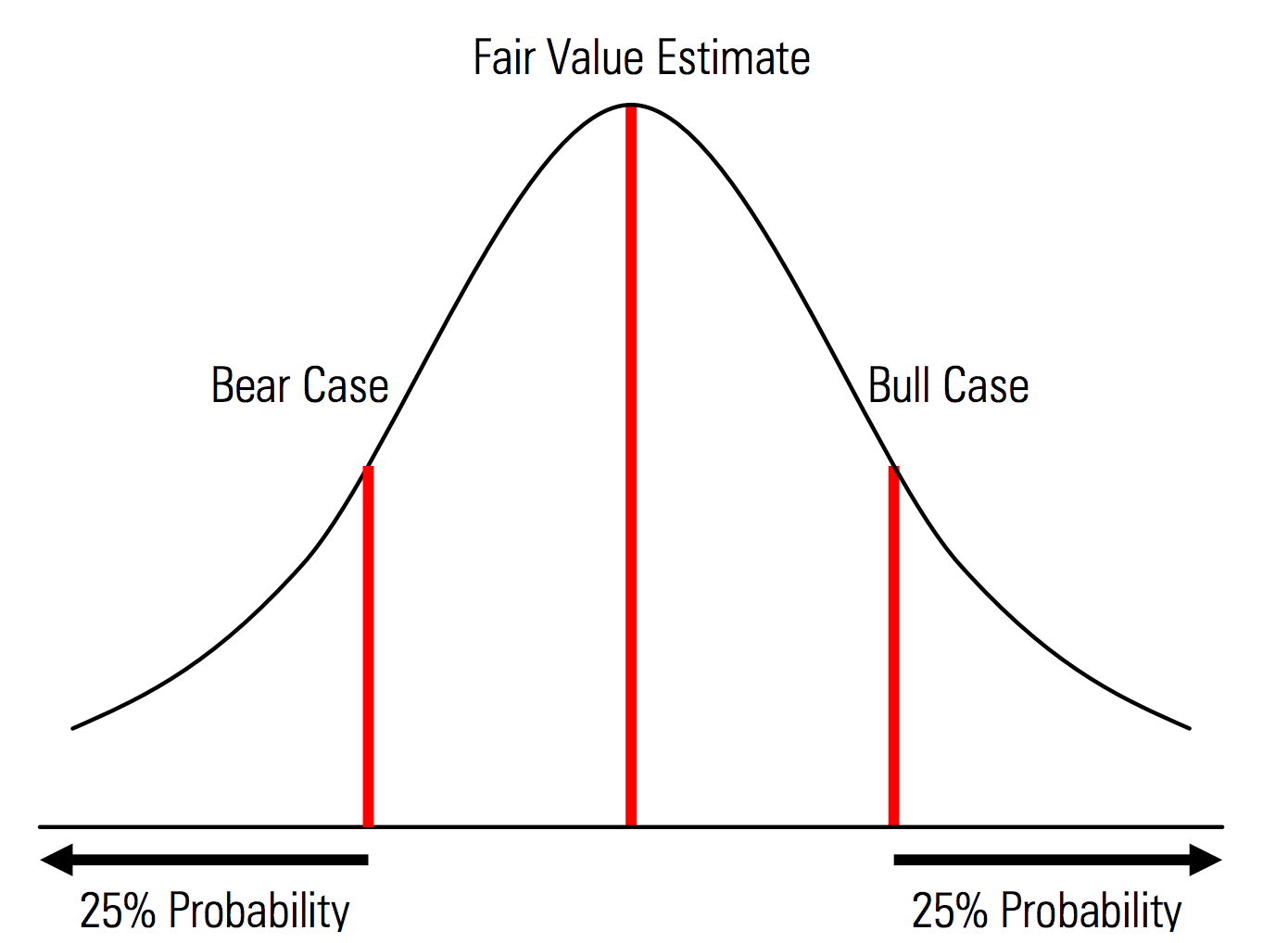
Olasılık dağılımlarını ve Monte Carlo simülasyonlarını kullanma. Olasılık dağılımlarını kullanmak, tahmindeki tüm olası sonuçları modellemenize ve görselleştirmenize olanak tanır. Bu, yalnızca toplu düzeyde değil, aynı zamanda ayrıntılı bireysel girdiler, varsayımlar ve itici güçler için de yapılabilir. Monte Carlo yöntemleri daha sonra, birkaç belirsiz değişkenin genel sonuçların belirsizliğine nasıl katkıda bulunduğunun analizine izin vererek, toplam bir düzeyde elde edilen olasılık dağılımlarını hesaplamak için kullanılır. Belki de en önemlisi, yaklaşım, analize ve karara dahil olan herkesi, tahminin doğasında bulunan belirsizliği açıkça tanımaya ve olasılıklar içinde düşünmeye zorlar. Tıpkı diğer yaklaşımlarda olduğu gibi bunun da sakıncaları vardır, bunlar arasında yanlış kesinlik ve daha karmaşık bir modelin kullanılmasıyla ortaya çıkabilecek aşırı güven riski ve aksi takdirde yalnızca nokta tahminlerinin olacağı durumlarda uygun olasılık dağılımlarını seçmek ve parametrelerini tahmin etmek için gereken ek çalışma vardır. Kullanılmış.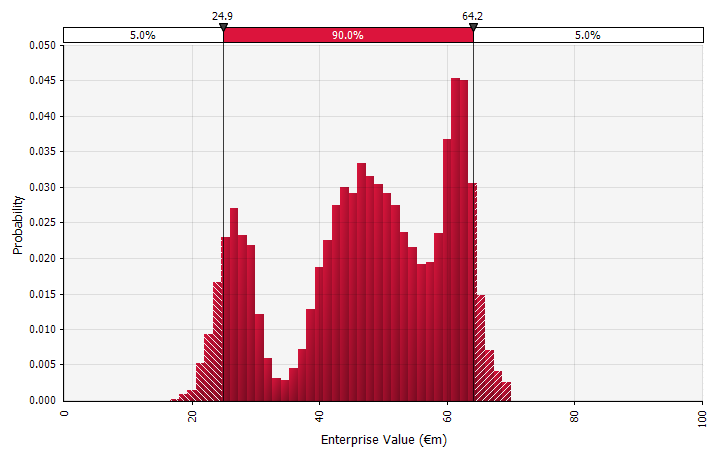

Monte Carlo Simülasyonu Nedir?

Monte Carlo simülasyonları, finansal tahminlerde ve tahminlerde farklı sonuçların olasılığını modeller. Adlarını, Monaco'nun üst düzey kumarhaneleriyle dünyaca ünlü Monte Carlo bölgesinden alırlar; Rastgele sonuçlar, rulet ve slot makinelerinde olduğu gibi, tekniğin merkezindedir. Monte Carlo simülasyonları, mühendislik, proje yönetimi, petrol ve gaz arama ve diğer sermaye yoğun endüstriler, Ar-Ge ve sigorta dahil olmak üzere çok çeşitli alanlarda faydalıdır; Burada finans ve iş alanındaki uygulamalara odaklanıyorum.

Olasılık Dağılımları

Simülasyonda belirsiz girdiler, ortalama ve standart sapma gibi parametrelerle tanımlanan olasılık dağılımları kullanılarak tanımlanır. Mali projeksiyonlardaki örnek girdiler, gelir ve marjlardan emtia fiyatları, genişleme için sermaye harcamaları veya döviz kurları gibi daha ayrıntılı bir şeye kadar herhangi bir şey olabilir.

Bir veya daha fazla girdi olasılık dağılımı olarak tanımlandığında, çıktı da bir olasılık dağılımı olur. Bir bilgisayar her girdi dağılımından rastgele bir sayı çeker ve sonucu hesaplar ve kaydeder. Bu, her biri bir yineleme olarak adlandırılan yüzlerce, binlerce veya on binlerce kez tekrarlanır. Birlikte alındığında, bu yinelemeler, nihai sonucun olasılık dağılımına yaklaşır.

Girdi Türleri

Girdi dağılımları, rastgele oluşturulmuş değerin dağılım altında herhangi bir değeri alabileceği (örneğin normal bir dağılım) sürekli veya olasılıkların iki veya daha fazla farklı senaryoya eklendiği ayrık olabilir.

Bir simülasyon, farklı türlerdeki dağılımların bir karışımını da içerebilir. Örneğin, her biri ayrı bir başarı veya başarısızlık olasılığına sahip birkaç aşamalı bir farmasötik Ar-Ge projesini ele alalım. Bu, her aşama için ihtiyaç duyulan belirsiz yatırım miktarlarını ve proje pazara ulaşan bir ürünle sonuçlanırsa potansiyel gelirleri açıklayan sürekli dağıtımlarla birleştirilebilir. Aşağıdaki grafik böyle bir simülasyondan elde edilen çıktıyı göstermektedir: 5 milyon € ila 50 milyon € (mevcut değer) arasındaki tüm yatırımı kaybetme olasılığı ~%65 ve büyük olasılıkla aşağıdaki aralıkta net kazanç ~%35 100 € ila 250 € - MIRR veya NPV gibi temel çıktı ölçümleri olasılık dağılımları yerine nokta tahminleri olarak gösterilirse kaybolacak bilgiler.

Uygulamada Monte Carlo Simülasyonları

Monte Carlo simülasyonlarının daha yaygın olarak kullanılmamasının bir nedeni, tipik finans günlük araçlarının onları çok iyi desteklememesidir. Excel ve Google E-Tablolar, her hücrede bir sayı veya formül sonucu tutar ve olasılık dağılımlarını tanımlayıp rastgele sayılar üretebilseler de, Monte Carlo işlevselliği ile sıfırdan bir finansal model oluşturmak zahmetlidir. Ve birçok finans kurumu ve yatırım firması türevleri değerlemek, portföyleri analiz etmek ve daha fazlası için Monte Carlo simülasyonlarını kullanırken, araçları genellikle şirket içinde geliştirilir, tescilli veya aşırı pahalıdır; bu da onları bireysel finans profesyonelleri için erişilemez hale getirir.

Bu nedenle, Monte Carlo simülasyonlarıyla çalışmayı büyük ölçüde kolaylaştıran ve bunları mevcut modellerinize entegre etmenize olanak tanıyan @RISK by Palisade, ModelRisk by Vose ve RiskAMP gibi Excel eklentilerine dikkat çekmek istiyorum. Aşağıdaki örnekte @RISK kullanacağım.

Örnek olay: Monte Carlo Simülasyonu ile Nakit Akışı Projeksiyonları

Bir Monte Carlo simülasyonunun temel kavramlarını gösteren basit bir örneği inceleyelim: beş yıllık bir nakit akışı tahmini. Bu kılavuzda, değerleme amaçları için temel bir nakit akışı modeli kurup dolduruyorum, girdileri kademeli olarak olasılık dağılımlarıyla değiştiriyorum ve son olarak simülasyonu çalıştırıyorum ve sonuçları analiz ediyorum.

Adım 1. Modeli Seçme veya Oluşturma

Başlangıç ​​olarak, olasılık dağılımlarını kullanmanın temel özelliklerini vurgulamaya odaklanan basit bir model kullanıyorum. Başlangıç ​​olarak, bu modelin diğer Excel modellerinden hiçbir farkı olmadığını unutmayın; yukarıda bahsettiğim eklentiler mevcut modellerinizle ve elektronik tablolarınızla çalışır. Aşağıdaki model, bir senaryo oluşturmak için varsayımlarla doldurulmuş basit bir hazır sürümdür.

Adım 2. İlk Olasılık Dağılımını Oluşturma

İlk önce varsayımlarımızı yapmak için gerekli bilgileri toplamamız gerekiyor, ardından eklemek için doğru olasılık dağılımlarını seçmemiz gerekiyor. Belirsizliği ele almak için hangi yaklaşımı seçerseniz seçin, temel girdilerin/varsayımların kaynağının aynı olduğuna dikkat etmek önemlidir. Öngörülen pazar gelişimi, endüstri eğilimleri ve rekabet dinamikleri bağlamında şirketin iş planının kapsamlı bir incelemesi olan ticari durum tespiti, tipik olarak geçmiş verilerden ekstrapolasyon, uzman görüşü dahil etme, pazar araştırması yürütme ve pazar katılımcıları ile görüşme içerir. Tecrübelerime göre, uzmanlar ve piyasa katılımcıları farklı senaryoları, riskleri ve çeşitli sonuçları tartışmaktan mutluluk duyarlar. Bununla birlikte, çoğu olasılık dağılımlarını açıkça tanımlamaz.

Şimdi, ilk tahmin yılı (2018) için tahmini satış artışından başlayarak, ana girdi değerlerimizi olasılık dağılımlarıyla tek tek gözden geçirelim ve değiştirelim. Excel için @RISK eklentisi 15 günlük ücretsiz deneme ile değerlendirilebilir, böylece Palisade web sitesinden indirebilir ve birkaç tıklama ile kurabilirsiniz. @RISK eklentisi etkinken, dağıtımı istediğiniz hücreyi seçin ve menüden "Dağıtımı tanımla"yı seçin.

Daha sonra çıkan dağıtım paletinden birini seçersiniz. @RISK yazılımı, aralarından seçim yapabileceğiniz 70'den fazla farklı dağıtım sunar, bu nedenle birini seçmek ilk başta bunaltıcı görünebilir. Aşağıda en sık kullandığım bir avuç için bir rehber var:

Normal. Ortalama ve standart sapma ile tanımlanır. Bu, basitliği nedeniyle iyi bir başlangıç ​​noktasıdır ve belirli bir girdi için belki de önceden tanımlanmış senaryoları veya aralıkları kapsayan bir dağıtım tanımladığınız, durumların temel durum etrafında simetrik olmasını ve her bir kuyruktaki olasılıkların makul göründüğünü (Morningstar örneğinde olduğu gibi %25 diyelim).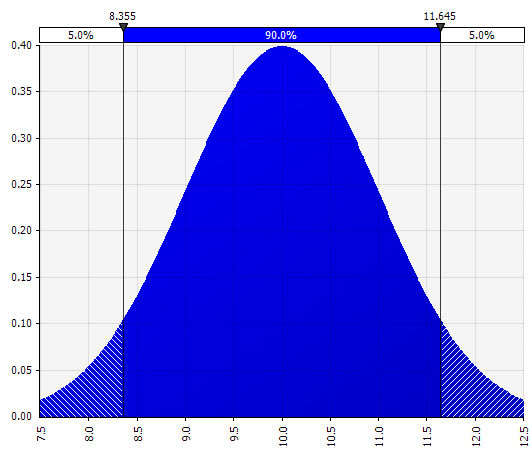
Johnson Anları. Bunu seçmek, eğri dağılımları ve daha kalın veya daha ince kuyruklu dağılımları tanımlamanıza olanak tanır (teknik olarak çarpıklık ve basıklık parametreleri ekleyerek). Perde arkasında, bu, seçilen dört parametreyi yansıtan dört dağılımdan birini seçmek için bir algoritma kullanır, ancak bu kullanıcı tarafından görülmez --- odaklanmamız gereken tek şey parametrelerdir. Bazen girdi için bilgi toplama sürecinde normal dağılımın uygun olmadığı anlaşılır. Örneğin, bir endüstri döngüsünün dip noktasında veya zirvesinde olan bir şirket için, önümüzdeki beş yıl boyunca daha iyi veya daha kötü performans olasılığı simetrik olmayacaktır. Zirveye ne kadar yakınsa, devam eden güçlü performansa karşı bir gerileme o kadar olasıdır. Bu, çarpık bir dağılımın yararlı olabileceği yerdir. Finansın birçok alanında "yağ kuyrukları" kavramı hakkında çok şey yazıldı. Çok nadir olması gereken olayların normal bir dağılımın gösterdiğinden daha sık meydana gelmesiyle, normal dağılımın çoğu zaman gerçek sonuçları çok iyi tanımlamadığı görülmektedir.
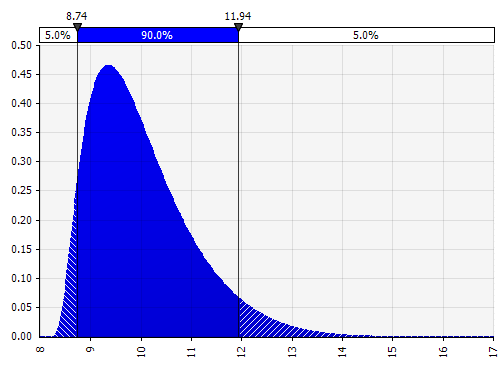Ayrık. Olasılıkların iki veya daha fazla spesifik değere verildiği yer. Başlangıçtaki aşamalı Ar-Ge projesi örneğine dönersek, her aşamada başarı olasılığı, 1'in başarıyı ve 0 başarısızlığı temsil ettiği bir ikili ayrık dağılım olarak modellenir.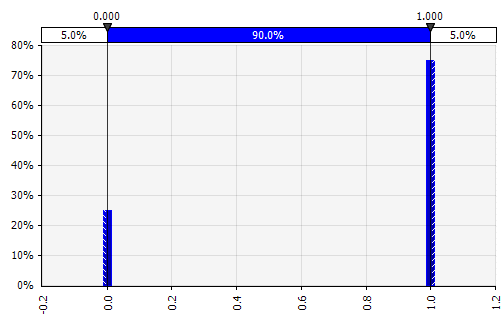
Dağıtım Uydurma. Çok sayıda geçmiş veri noktanız olduğunda, dağıtım uydurma işlevi kullanışlıdır. Bu, örneğin üç veya dört yıllık tarihsel satış büyümesi anlamına gelmez, ancak emtia fiyatları, döviz kurları veya tarihin gelecekteki eğilimler ve belirsizlik derecesi hakkında yararlı bilgiler verebileceği diğer piyasa fiyatları gibi zaman serisi verileri anlamına gelir.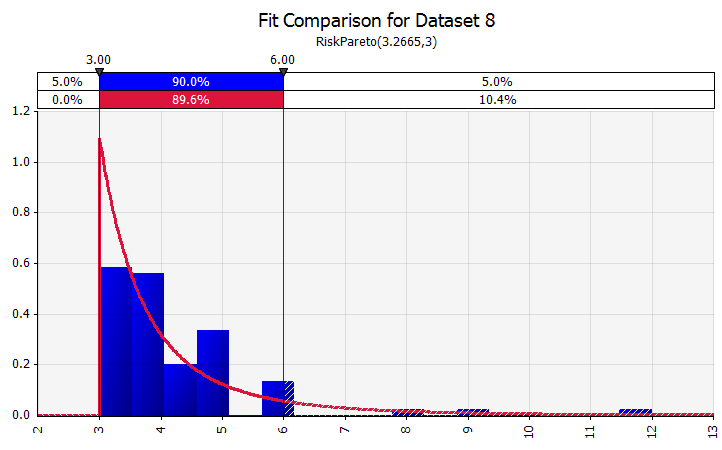
Birkaç farklı dağıtımı tek bir dağıtımda birleştirmek. Bireysel önyargıların potansiyel etkisini azaltmak için, farklı kaynakların girdilerini bir varsayıma dahil etmek ve/veya bulguları gözden geçirip tartışmak genellikle iyi bir fikirdir. Farklı yaklaşımlar vardır: 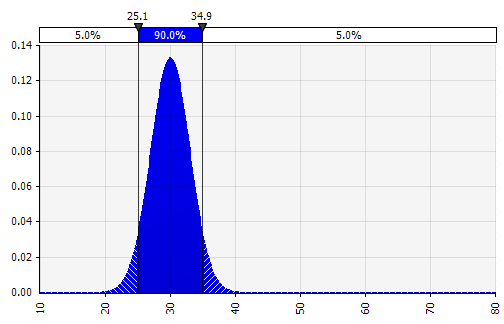Bir taslak veya ilk görüş hazırlayın ve ardından uzmanlarla, daha geniş yönetim ekibiyle veya diğer karar vericilerle gözden geçirin. Bir toplantıda ortaklaşa en önemli dağıtımları geliştirin. Bu, iyi bir tartışmaya ve daha iyi sonuçlara yol açabilir, ancak her zaman olduğu gibi grubun bileşimi çok önemlidir; temsil edilen farklı bakış açılarına/işlevlere sahip olmak ve güçlü ancak saygılı bir tartışma ortamını teşvik etmek elbette yardımcı olur. Her bir anahtar kaynak için bir dağıtım geliştirin ve her birine ne kadar inandığınıza göre ağırlıklandırarak bunları birleştirin. Birkaç farklı uzmandan girdi alıyorsanız, her birinin diğerlerinden bağımsız olarak kendi görüşlerini sunmasına izin vermek ve daha sonra bir araya getirmek iyi bir fikir olabilir. @RISK işlevi MakeRiskInput bunu bizim için yapar.	Ağırlık: 20% 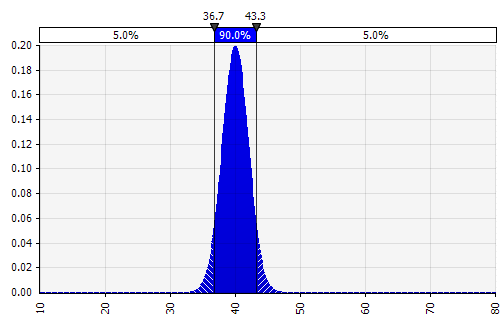+ Ağırlık: 20% 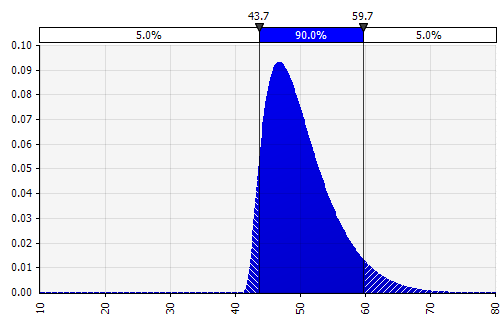+ Ağırlık: %60 =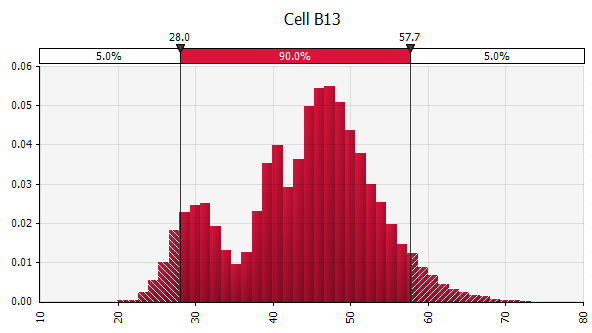
Serbest el. Tartışmaların bir parçası olarak bir dağıtımı hızlı bir şekilde göstermek için veya mevcut paletten kolayca oluşturulamayan bir model hazırlarken bir dağıtıma ihtiyacınız varsa, serbest el işlevi kullanışlıdır. Adından da anlaşılacağı gibi, bu, basit bir boyama aracı kullanarak dağılımı çizmenize olanak tanır.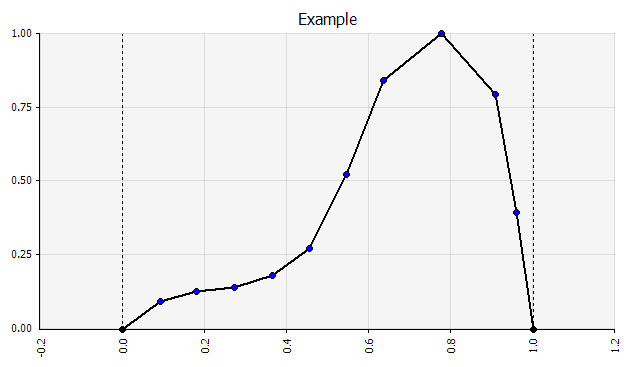

Şimdi, sol tarafta birkaç parametre ile dağılımın bir görselleştirmesini görüyoruz. Ortalama ve standart sapma sembolleri tanıdık gelmelidir. Normal dağılım durumunda, ortalama, hücreye daha önce tek bir değer olarak girdiğimiz değer olacaktır. Örnek olarak, %10'luk ortalamayı temsil eden 2018 satış olasılık dağılımı. Tipik modeliniz ya sadece %10 rakamına odaklanacak ya da sırasıyla %15 ve %5 büyüme ile "boğa" ve "ayı" senaryolarına sahip olsa da, bu şimdi tüm beklenen potansiyel sonuçlar hakkında bilgi sağlıyor.

Monte Carlo simülasyonlarının bir faydası, düşük olasılıklı kuyruk sonuçlarının düşünme ve tartışmaları tetikleyebilmesidir. Yalnızca yukarı ve aşağı senaryoları görüntülemek, karar vericilerin bunları dış sınırlar olarak yorumlaması ve dışarıda kalan senaryoları göz ardı etmesi riskini ortaya çıkarabilir. Bu, kuruluşun veya bireyin risk toleransının ötesindeki sonuçlara maruz kalma ile hatalı karar vermeyle sonuçlanabilir. Söz konusu senaryonun feci sonuçları olacaksa, %5 veya %1'lik bir olasılık bile kabul edilemez olabilir.

Adım 3. Gelir Tahminini Bir Yıldan Birkaç Yıla Genişletme

Monte Carlo modellemesiyle, zaman içinde olduğu gibi, belirsizlik ve olasılık dağılımlarının nasıl üst üste yığıldığına dikkat edin. Bir örneği gözden geçirelim. Her yıl satışlar önceki yıllardaki büyümeye bağlı olduğundan, 2022 satış tahminimizin 2018'e göre daha belirsiz olduğunu görselleştirebilir ve görebiliriz (her yıl için standart sapmalar ve %95 güven aralıkları kullanılarak gösterilmiştir). Basitlik adına, aşağıdaki örnekte bir yıl olan 2018 için büyüme belirtilir ve ardından aynı büyüme oranı 2022'ye kadar sonraki yılların her birine uygulanır. Diğer bir yaklaşım, her yıl için bir tane olmak üzere beş bağımsız dağılıma sahip olmaktır.

Adım 4. Gelir Tablosuna Devam Etme—Marjları Olasılık Dağılımları Olarak İfade Etme

Şimdi, satış büyümesi için yaptığımıza benzer şekilde, 2018'deki FVÖK marjı için (aşağıda vurgulanmıştır) bir olasılık dağılımı tahmin ediyoruz.

Burada, göreceli pazar payı ile karlılık arasında ölçek ekonomilerini yansıtan açık bir korelasyonun olduğu bir durumu simüle etmek için korelasyon fonksiyonunu kullanabiliriz. Pazara göre daha yüksek satış büyümesi ve buna bağlı olarak daha yüksek pazar payına sahip senaryolar, daha yüksek FVÖK marjları ile pozitif bir korelasyona sahip olacak şekilde modellenebilir. Bir firmanın servetinin petrol fiyatları veya döviz kurları gibi diğer bazı dış faktörlerle güçlü bir şekilde ilişkili olduğu endüstrilerde, bu faktör için bir dağılım tanımlamak ve satışlar ve karlılık ile bir korelasyon modellemek mantıklı olabilir.

Mevcut zamana, işlemin boyutuna ve diğer faktörlere bağlı olarak, genellikle bir işletim modeli oluşturmak ve en belirsiz değişkenleri açıkça girmek mantıklıdır. Bunlar şunları içerir: ürün hacimleri ve fiyatları, emtia fiyatları, döviz kurları, temel genel gider kalemleri, aylık aktif kullanıcılar ve birim başına ortalama gelir (ARPU). Geliştirme süresi, pazara sunma süresi veya pazar benimseme oranı gibi miktarın ötesinde değişkenleri modellemek de mümkündür.

Adım 5. Bilanço ve Nakit Akış Tablosu

Ana hatlarıyla belirtilen yaklaşımı kullanarak, artık varsayımlarla doldurarak ve mantıklı olduğu yerlerde olasılık dağılımlarını kullanarak bilanço ve nakit akış tablosu üzerinden devam edebiliriz.

Sermaye harcaması ile ilgili bir not: bu, potansiyel olarak daha büyük kademeli yatırımlarla birlikte mutlak tutarlar veya satış yüzdesi olarak modellenebilir; örneğin bir üretim tesisi, net bir kapasite sınırına ve büyük bir genişleme yatırımına veya satışlar eşiği aştığında gerekli olan yeni bir tesise sahip olabilir. Söz konusu 1.000 veya 10.000 iterasyonun her biri modelin tamamen yeniden hesaplanması olacağından, belirli bir hacme ulaşıldığında/olduğunda yatırım maliyetini tetikleyen basit bir formül kullanılabilir.

Adım 6. Modelin Sonlandırılması

Monte Carlo modelinin oluşturulması, standart bir finansal modele kıyasla ek bir adıma sahiptir: Sonuçları değerlendirmek istediğimiz hücrelerin özellikle çıktı hücreleri olarak atanması gerekir. Yazılım, simülasyon bittikten sonra değerlendirmemiz için bu hücreler için simülasyonun her yinelemesinin sonuçlarını kaydedecektir. Tüm modeldeki tüm hücreler her yinelemede yeniden hesaplanır, ancak giriş veya çıkış hücreleri olarak belirlenmeyen diğer hücrelerdeki yinelemelerin sonuçları kaybolur ve simülasyon bittikten sonra analiz edilemez. Aşağıdaki ekran görüntüsünde de görebileceğiniz gibi, MIRR sonuç hücresini çıkış hücresi olarak belirliyoruz.

Modeli oluşturmayı bitirdikten sonra, “simülasyonu başlat” a basarak ve birkaç saniye bekleyerek simülasyonu ilk kez çalıştırmanın zamanı geldi.

Adım 7. Sonuçların Yorumlanması

Olasılıklar Olarak İfade Edilen Çıktılar. Modelimiz daha önce değiştirilmiş IRR için bize tek bir değer verirken, şimdi bu değer etrafında farklı olasılıklara sahip bir dizi potansiyel sonuç olduğunu açıkça görebiliyoruz. Bu, “Bu yatırımla engelli getiri oranımıza ulaşacak mıyız?” gibi soruları yeniden ifade etmemize olanak tanır. “Engel oranımızı yakalama veya aşma olasılığımız ne kadar?” Örneğin, bir güven aralığı kullanarak hangi sonuçların daha olası olduğunu keşfedebilirsiniz. Görselleştirme, sonuçları farklı paydaşlara iletirken yardımcı olur ve mevcut olanın diğerleriyle karşılaştırıldığında ne kadar çekici ve (belirsiz) olduğunu görsel olarak karşılaştırmak için diğer işlemlerden elde edilen çıktıları üst üste bindirebilirsiniz (aşağıya bakın).

Nihai sonuçtaki belirsizlik derecesini anlamak. Başlangıçta satışlar için yaptığımıza benzer şekilde, zaman içinde nakit akışı değişkenliği grafiği oluşturursak, satışlarda ve olasılık dağılımları olarak modellediğimiz diğer girdilerde nispeten mütevazı bir belirsizlikle bile serbest nakit akışındaki değişkenliğin önemli hale geldiği netleşir. , ortalamadan sadece bir standart sapma bile olsa, yaklaşık 0,5 milyon € ile 5,0 milyon € arasında değişen sonuçlarla (10 kat bir faktör). Bu, belirsiz varsayımların üst üste yığılmasının bir sonucudur; bu, yıllar içinde hem "dikey" hem de mali tablolar aracılığıyla "yatay" olarak birleşen bir etkidir. Görselleştirmeler, her iki belirsizlik türü hakkında bilgi sağlar.

Duyarlılık analizi: Tornado grafiğine giriş. Bir diğer önemli alan, nihai sonucunuz üzerinde hangi girdilerin en büyük etkiye sahip olduğunu anlamaktır. Klasik bir örnek, nakit akışı tahminine göre iskonto oranı veya nihai değer varsayımlarının önemine genellikle çok az ağırlık verilmesidir. Bunu ele almanın yaygın bir yolu, her eksene bir tuş girişi koyduğunuz ve ardından her hücrede sonucu hesapladığınız matrisleri kullanmaktır (aşağıya bakın). Bu, özellikle kararların bir veya birkaç temel varsayıma bağlı olduğu durumlarda faydalıdır - bu “inanmanız gereken şey” durumlarında, (örneğin) bir yatırım komitesindeki veya bir üst yönetim ekibindeki karar vericiler, farklı görüşlere sahip olabilir. bu temel varsayımlar ve yukarıdaki gibi bir matris, her birinin kendi görüşlerine karşılık gelen bir sonuç değeri bulmasına izin verir ve buna dayanarak karar verebilir, oy verebilir veya tavsiye verebilir.

Monte Carlo simülasyonları ile geliştirme. Monte Carlo simülasyonlarını kullanırken, bu yaklaşım başka bir yaklaşımla tamamlanabilir: kasırga diyagramı. Bu görselleştirme, farklı belirsiz girdileri ve varsayımları dikey eksende listeler ve ardından her birinin nihai sonuç üzerindeki etkisinin ne kadar büyük olduğunu gösterir.

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein