Forecaster's Toolbox: So führen Sie Monte-Carlo-Simulationen durch

Zusammenfassung

Einführung

Erstens ist die einzige Gewissheit, dass es keine Gewissheit gibt. Zweitens ist jede Entscheidung als Konsequenz eine Frage der Abwägung von Wahrscheinlichkeiten. Drittens müssen wir trotz Ungewissheit entscheiden und handeln. Und schließlich müssen wir Entscheidungen nicht nur anhand der Ergebnisse beurteilen, sondern auch daran, wie diese Entscheidungen getroffen wurden. – Robert E. Rubin

Einer der wichtigsten und herausforderndsten Aspekte der Prognose ist der Umgang mit der Unsicherheit, die der Untersuchung der Zukunft innewohnt. Nachdem ich seit 2003 Hunderte von Finanz- und Betriebsmodellen für LBOs, Startup-Fundraisings, Budgets, M&A und strategische Unternehmenspläne erstellt und ausgefüllt habe, habe ich eine breite Palette von Ansätzen dafür erlebt. Jeder CEO, CFO, Vorstandsmitglied, Investor oder Anlageausschussmitglied bringt seine eigene Erfahrung und Herangehensweise an Finanzprognosen und Unsicherheiten ein – beeinflusst von unterschiedlichen Anreizen. Häufig bietet der Vergleich tatsächlicher Ergebnisse mit Prognosen eine Einschätzung dafür, wie groß die Abweichungen zwischen Prognosen und tatsächlichen Ergebnissen sein können, und daher die Notwendigkeit, Unsicherheiten zu verstehen und explizit zu erkennen.

Ich habe anfangs mit Szenario- und Sensitivitätsanalysen begonnen, um Unsicherheiten zu modellieren, und halte sie immer noch für sehr nützliche Werkzeuge. Seit ich 2010 Monte-Carlo-Simulationen in meine Toolbox aufgenommen habe, habe ich festgestellt, dass sie ein äußerst effektives Werkzeug sind, um zu verfeinern und zu verbessern, wie Sie über Risiken und Wahrscheinlichkeiten denken. Ich habe den Ansatz für alles verwendet, von der Erstellung von DCF-Bewertungen, der Bewertung von Kaufoptionen bei Fusionen und Übernahmen und der Diskussion von Risiken mit Kreditgebern bis hin zur Suche nach Finanzierung und der Leitung der Zuweisung von VC-Finanzierung für Startups. Der Ansatz wurde von Vorstandsmitgliedern, Investoren und leitenden Managementteams immer gut aufgenommen. In diesem Artikel stelle ich eine schrittweise Anleitung zur Verwendung von Monte-Carlo-Simulationen in der Praxis zur Verfügung, indem ich ein DCF-Bewertungsmodell aufbaue.

Jede Entscheidung ist eine Frage der Abwägung von Wahrscheinlichkeiten

Bevor wir mit der Fallstudie beginnen, lassen Sie uns einige verschiedene Ansätze zum Umgang mit Ungewissheit betrachten. Das Konzept des erwarteten Werts – der wahrscheinlichkeitsgewichtete Durchschnitt der Cashflows in allen möglichen Szenarien – ist Finance 101. Aber Finanzfachleute und Entscheidungsträger im weiteren Sinne verfolgen sehr unterschiedliche Ansätze, wenn sie diese einfache Erkenntnis in die Praxis umsetzen. Der Ansatz kann vom schlichten Nichterkennen oder Diskutieren von Ungewissheit auf der einen Seite bis hin zu ausgefeilten Modellen und Software auf der anderen Seite reichen. In einigen Fällen verbringen die Leute am Ende mehr Zeit damit, Wahrscheinlichkeiten zu diskutieren, als Cashflows zu berechnen.

Abgesehen davon, dass wir es einfach nicht ansprechen, wollen wir einige Möglichkeiten untersuchen, wie mit Unsicherheit in mittel- oder langfristigen Projektionen umgegangen werden kann. Viele davon dürften Ihnen bekannt sein.

Erstellen eines Szenarios. Dieser Ansatz ist die Standardeinstellung für Budgets, viele Startups und sogar Investitionsentscheidungen. Abgesehen davon, dass sie keine Informationen über den Grad der Ungewissheit oder Erkenntnis enthalten, dass die Ergebnisse von den Prognosen abweichen können, können sie mehrdeutig sein und je nach Interessenvertreter unterschiedlich interpretiert werden. Einige mögen es als ein erweitertes Ziel interpretieren, bei dem das tatsächliche Ergebnis eher unterschritten als überschritten wird. Einige betrachten es als Basisleistung mit mehr Aufwärts- als Abwärtswerten. Andere sehen es möglicherweise als "Basisfall" mit einer Wahrscheinlichkeit von 50/50 nach oben und unten. Bei einigen Ansätzen, insbesondere für Startups, ist es sehr ehrgeizig und ein Scheitern oder Unterschreiten ist bei weitem das wahrscheinlichere Ergebnis, aber ein höherer Diskontierungssatz wird verwendet, um das Risiko zu berücksichtigen.	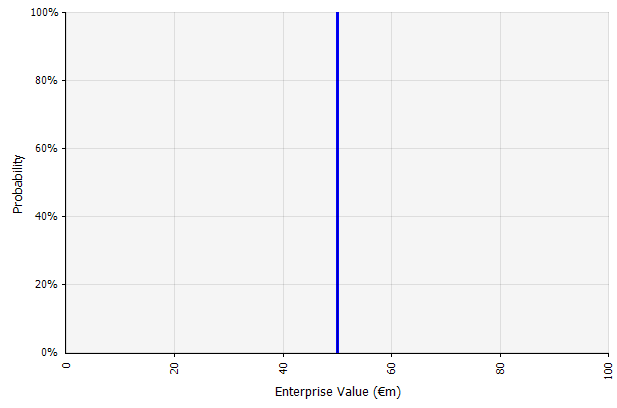Die Eingaben in die langfristige Cashflow-Prognose bei diesem Ansatz sind allesamt Punktschätzungen, die in diesem Beispiel mit einer impliziten Wahrscheinlichkeit von 100 % ein Punktschätzungsergebnis von 50 Mio. € ergeben.
Erstellen mehrerer Szenarien. Dieser Ansatz erkennt an, dass sich die Realität wahrscheinlich nicht nach einem einzigen vorgegebenen Plan entwickeln wird. 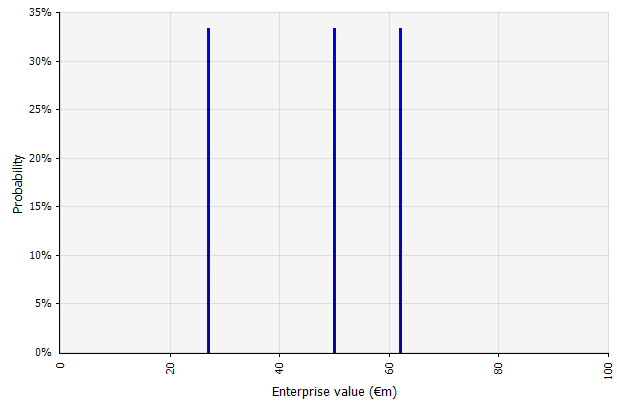In ihrer einfachsten Form, der Sensitivitätsanalyse, könnte dies die Auswirkungen von beispielsweise einem Umsatzwachstum von 10 % über und unter dem Basisfall simulieren, wobei eine bestimmte Mischung aus festen, halbvariablen und variablen Kosten zur Schätzung des Endergebnisses verwendet wird Einschlag. In komplexeren Formen denken Sie für jedes Szenario aus einer ganz anderen Perspektive in die Zukunft und analysieren die Auswirkungen, die unterschiedliche technologische Entwicklungen, Wettbewerbsdynamiken und Makrotrends auf die Leistung des Unternehmens haben werden. Leider werden die Szenarien oft recht willkürlich gewählt, manchmal auch mit Blick auf ein gewünschtes Endergebnis.	Die drei unterschiedlichen Szenarien ergeben drei unterschiedliche Ergebnisse, die hier als gleich wahrscheinlich angenommen werden. Die Wahrscheinlichkeiten von Ergebnissen außerhalb der Hoch- und Niedrigszenarien werden nicht berücksichtigt.
Erstellen von Basis-, Aufwärts- und Abwärtsfällen mit explizit erkannten Wahrscheinlichkeiten. Das heißt, die Bear- und Bull-Fälle enthalten beispielsweise eine Wahrscheinlichkeit von 25 % in jedem Tail, und die Fair-Value-Schätzung stellt den Mittelpunkt dar. Ein nützlicher Vorteil davon aus Sicht des Risikomanagements ist die explizite Analyse des Tail-Risikos, dh Ereignisse außerhalb der Aufwärts- und Abwärtsszenarien.	Abbildung aus dem Bewertungshandbuch von Morningstar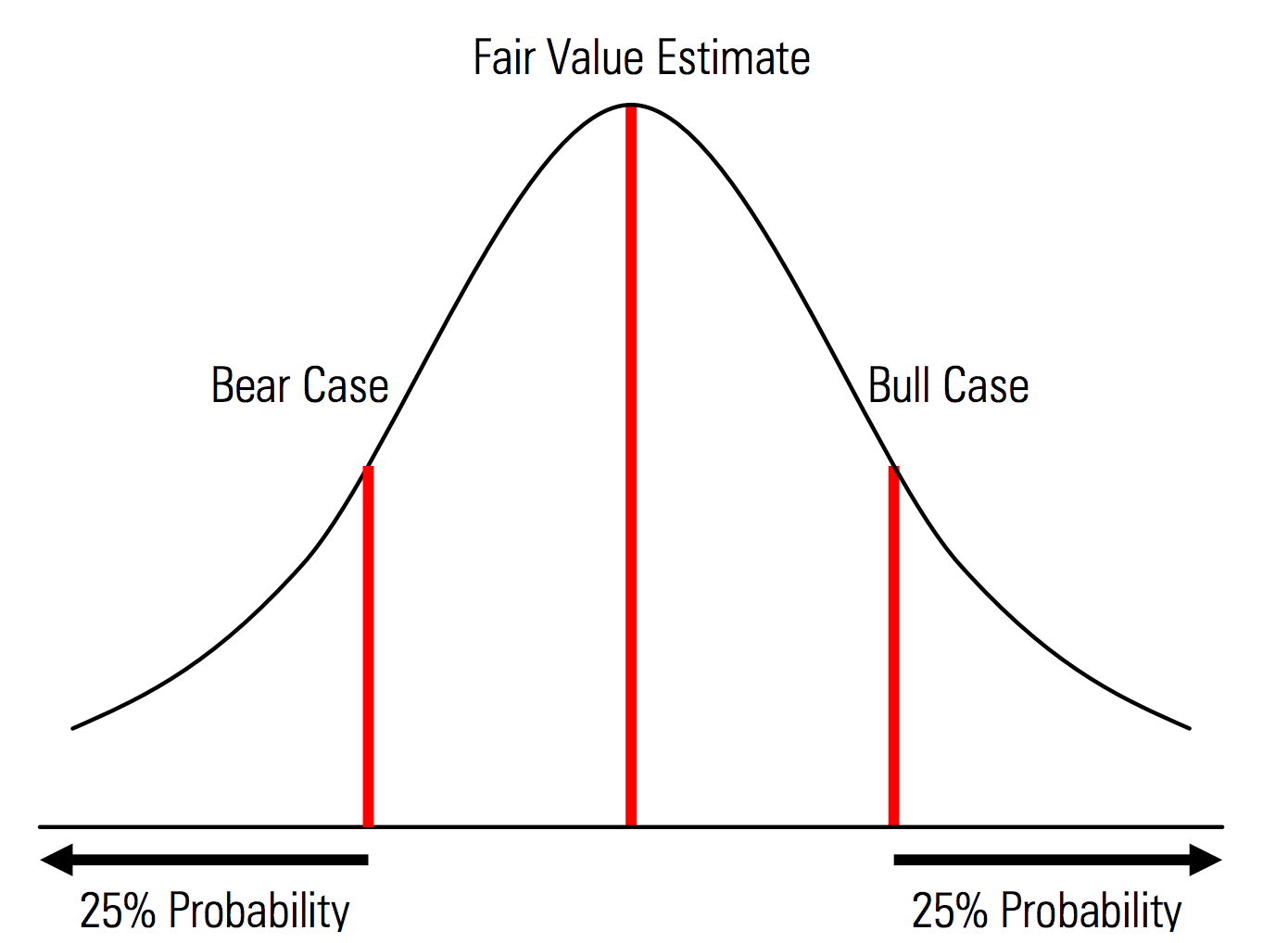
Verwendung von Wahrscheinlichkeitsverteilungen und Monte-Carlo-Simulationen. Durch die Verwendung von Wahrscheinlichkeitsverteilungen können Sie die gesamte Bandbreite möglicher Ergebnisse in der Prognose modellieren und visualisieren. Dies kann nicht nur auf aggregierter Ebene erfolgen, sondern auch für detaillierte individuelle Eingaben, Annahmen und Treiber. Anschließend werden Monte-Carlo-Methoden verwendet, um die resultierenden Wahrscheinlichkeitsverteilungen auf aggregierter Ebene zu berechnen, wodurch analysiert werden kann, wie mehrere unsichere Variablen zur Unsicherheit der Gesamtergebnisse beitragen. Am wichtigsten ist vielleicht, dass der Ansatz alle an der Analyse und Entscheidung Beteiligten dazu zwingt, die der Prognose innewohnende Unsicherheit explizit anzuerkennen und in Wahrscheinlichkeiten zu denken. Genau wie die anderen Ansätze hat dies seine Nachteile, einschließlich des Risikos falscher Genauigkeit und daraus resultierender Selbstüberschätzung, die mit der Verwendung eines ausgefeilteren Modells einhergehen können, und der zusätzlichen Arbeit, die erforderlich ist, um geeignete Wahrscheinlichkeitsverteilungen auszuwählen und ihre Parameter zu schätzen, wo sonst nur Punktschätzungen wären benutzt.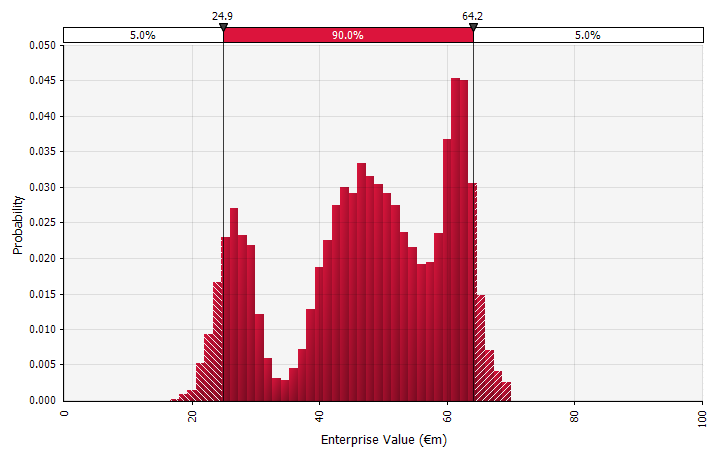

Was ist eine Monte-Carlo-Simulation?

Monte-Carlo-Simulationen modellieren die Wahrscheinlichkeit unterschiedlicher Ergebnisse in Finanzprognosen und Schätzungen. Sie verdienen ihren Namen aus der Gegend von Monte Carlo in Monaco, die für ihre High-End-Casinos weltberühmt ist; Zufällige Ergebnisse stehen im Mittelpunkt der Technik, genau wie beim Roulette und Spielautomaten. Monte-Carlo-Simulationen sind in einer Vielzahl von Bereichen nützlich, darunter Engineering, Projektmanagement, Öl- und Gasexploration und andere kapitalintensive Branchen, F&E und Versicherungen; hier konzentriere ich mich auf Anwendungen im Finanz- und Wirtschaftsbereich.

Wahrscheinlichkeitsverteilungen

In der Simulation werden die unsicheren Eingaben durch Wahrscheinlichkeitsverteilungen beschrieben, die durch Parameter wie Mittelwert und Standardabweichung beschrieben werden. Beispiele für Eingaben in Finanzprognosen können alles sein, von Einnahmen und Margen bis hin zu etwas Granularerem wie Rohstoffpreisen, Investitionsausgaben für eine Erweiterung oder Wechselkursen.

Wenn eine oder mehrere Eingaben als Wahrscheinlichkeitsverteilungen beschrieben werden, wird die Ausgabe ebenfalls zu einer Wahrscheinlichkeitsverteilung. Ein Computer zieht zufällig eine Zahl aus jeder Eingabeverteilung und berechnet und speichert das Ergebnis. Dies wird hundert-, tausend- oder zehntausendmal wiederholt, was jeweils als Iteration bezeichnet wird. Zusammengenommen nähern sich diese Iterationen der Wahrscheinlichkeitsverteilung des Endergebnisses an.

Arten von Eingängen

Die Eingabeverteilungen können entweder kontinuierlich sein, wobei der zufällig generierte Wert jeden Wert unterhalb der Verteilung annehmen kann (z. B. eine Normalverteilung), oder diskret sein, wobei Wahrscheinlichkeiten zwei oder mehr unterschiedlichen Szenarien zugeordnet sind.

Eine Simulation kann auch eine Mischung aus Verteilungen unterschiedlichen Typs enthalten. Nehmen wir zum Beispiel ein pharmazeutisches F&E-Projekt mit mehreren Phasen, die jeweils eine diskrete Erfolgs- oder Misserfolgswahrscheinlichkeit haben. Dies kann mit kontinuierlichen Ausschüttungen kombiniert werden, die ungewisse Investitionsbeträge beschreiben, die für jede Phase erforderlich sind, und potenzielle Einnahmen, wenn das Projekt zu einem Produkt führt, das auf den Markt kommt. Das folgende Diagramm zeigt das Ergebnis einer solchen Simulation: eine Wahrscheinlichkeit von ~65 %, die gesamte Investition von 5 bis 50 Millionen Euro (Barwert) zu verlieren, und eine Wahrscheinlichkeit von ~35 %, dass ein Nettogewinn höchstwahrscheinlich in der Größenordnung von 100 € bis 250 € – Informationen, die verloren gehen würden, wenn wichtige Output-Metriken wie MIRR oder NPV als Punktschätzungen und nicht als Wahrscheinlichkeitsverteilungen dargestellt würden.

Monte-Carlo-Simulationen in der Praxis

Ein Grund dafür, dass Monte-Carlo-Simulationen nicht weiter verbreitet sind, liegt darin, dass typische Tools für den Finanzalltag sie nicht sehr gut unterstützen. Excel und Google Sheets enthalten in jeder Zelle eine Zahl oder ein Formelergebnis, und obwohl sie Wahrscheinlichkeitsverteilungen definieren und Zufallszahlen generieren können, ist das Erstellen eines Finanzmodells mit Monte-Carlo-Funktionalität von Grund auf umständlich. Und während viele Finanzinstitute und Wertpapierfirmen Monte-Carlo-Simulationen zur Bewertung von Derivaten, zur Analyse von Portfolios und mehr verwenden, werden ihre Tools in der Regel intern entwickelt, sind proprietär oder unerschwinglich teuer, was sie für den einzelnen Finanzexperten unzugänglich macht.

Daher möchte ich auf Excel-Plugins wie @RISK von Palisade, ModelRisk von Vose und RiskAMP aufmerksam machen, die die Arbeit mit Monte-Carlo-Simulationen erheblich vereinfachen und es Ihnen ermöglichen, sie in Ihre bestehenden Modelle zu integrieren. In der folgenden exemplarischen Vorgehensweise verwende ich @RISK.

Fallstudie: Cashflow-Prognosen mit Monte-Carlo-Simulation

Sehen wir uns ein einfaches Beispiel an, das die Schlüsselkonzepte einer Monte-Carlo-Simulation veranschaulicht: eine Fünfjahres-Cashflow-Prognose. In dieser exemplarischen Vorgehensweise richte ich ein einfaches Cashflow-Modell für Bewertungszwecke ein und befülle es, ersetze die Eingaben schrittweise durch Wahrscheinlichkeitsverteilungen und führe schließlich die Simulation aus und analysiere die Ergebnisse.

Schritt 1. Auswahl oder Erstellung des Modells

Zu Beginn verwende ich ein einfaches Modell, das sich darauf konzentriert, die wichtigsten Merkmale der Verwendung von Wahrscheinlichkeitsverteilungen hervorzuheben. Beachten Sie, dass sich dieses Modell zunächst nicht von anderen Excel-Modellen unterscheidet. Die oben erwähnten Plugins funktionieren mit Ihren vorhandenen Modellen und Tabellenkalkulationen. Das folgende Modell ist eine einfache Standardversion, die mit Annahmen gefüllt ist, um ein Szenario zu bilden.

Schritt 2. Erstellen der ersten Wahrscheinlichkeitsverteilung

Zuerst müssen wir die Informationen sammeln, die für unsere Annahmen erforderlich sind, dann müssen wir die richtigen Wahrscheinlichkeitsverteilungen zum Einfügen auswählen. Es ist wichtig zu beachten, dass die Quelle der wichtigsten Eingaben/Annahmen die gleiche ist, unabhängig davon, welchen Ansatz Sie zum Umgang mit Unsicherheit wählen. Commercial Due Diligence, eine umfassende Überprüfung des Geschäftsplans des Unternehmens im Kontext der prognostizierten Marktentwicklung, Branchentrends und Wettbewerbsdynamik, umfasst typischerweise die Extrapolation aus historischen Daten, die Einbeziehung von Expertenmeinungen, die Durchführung von Marktforschung und die Befragung von Marktteilnehmern. Meiner Erfahrung nach diskutieren Experten und Marktteilnehmer gerne über verschiedene Szenarien, Risiken und Ergebnisbereiche. Die meisten beschreiben jedoch Wahrscheinlichkeitsverteilungen nicht explizit.

Lassen Sie uns nun durchgehen und unsere wichtigsten Eingabewerte nacheinander durch Wahrscheinlichkeitsverteilungen ersetzen, beginnend mit dem geschätzten Umsatzwachstum für das erste Prognosejahr (2018). Das @RISK-Plugin für Excel kann mit einer 15-tägigen kostenlosen Testversion evaluiert werden, sodass Sie es von der Palisade-Website herunterladen und mit wenigen Klicks installieren können. Wählen Sie bei aktiviertem @RISK-Plug-in die Zelle aus, in der die Verteilung erfolgen soll, und wählen Sie im Menü „Verteilung definieren“.

Sie wählen dann eine aus der angezeigten Palette von Distributionen aus. Die @RISK-Software bietet mehr als 70 verschiedene Distributionen zur Auswahl, so dass die Auswahl zunächst überwältigend erscheinen kann. Nachfolgend finden Sie eine Anleitung zu einer Handvoll, die ich am häufigsten verwende:

Normal. Definiert durch Mittelwert und Standardabweichung. Dies ist aufgrund seiner Einfachheit ein guter Ausgangspunkt und eignet sich als Erweiterung des Morningstar-Ansatzes, bei dem Sie eine Verteilung definieren, die möglicherweise bereits definierte Szenarien oder Bereiche für eine bestimmte Eingabe abdeckt, wobei sichergestellt wird, dass die Fälle um den Basisfall herum symmetrisch sind dass die Wahrscheinlichkeiten in jedem Ende vernünftig aussehen (z. B. 25 % wie im Morningstar-Beispiel).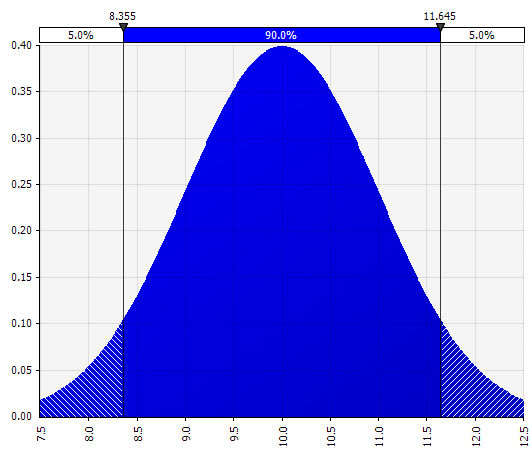
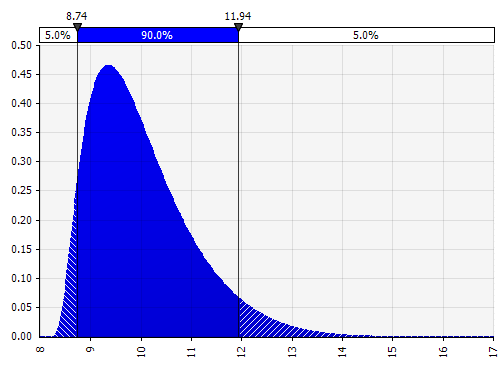
Johnson-Momente. Wenn Sie diese Option auswählen, können Sie schiefe Verteilungen und Verteilungen mit dickeren oder dünneren Enden definieren (technisch gesehen werden Schiefe- und Kurtosis-Parameter hinzugefügt). Hinter den Kulissen verwendet dies einen Algorithmus, um eine von vier Verteilungen auszuwählen, die die vier ausgewählten Parameter widerspiegelt, aber das ist für den Benutzer unsichtbar – wir müssen uns nur auf die Parameter konzentrieren. Manchmal wird beim Sammeln von Informationen für die Eingabe deutlich, dass die Normalverteilung nicht angemessen ist. Zum Beispiel werden für ein Unternehmen am Tiefpunkt oder Höhepunkt eines Branchenzyklus die Wahrscheinlichkeiten einer besseren oder schlechteren Performance in den nächsten, sagen wir, fünf Jahren nicht symmetrisch sein. Je näher am Höhepunkt, desto wahrscheinlicher ist ein Abschwung im Vergleich zu einer anhaltend starken Performance. Hier kann eine schiefe Verteilung nützlich sein. Über das Konzept der „Fat Tails“ ist in vielen Finanzbereichen viel geschrieben worden. Es scheint, dass die Normalverteilung die tatsächlichen Ergebnisse oft nicht sehr gut beschreibt, da Ereignisse, die sehr selten sein sollten, häufiger auftreten, als eine Normalverteilung vermuten lässt.
Diskret. Wo Wahrscheinlichkeiten für zwei oder mehr spezifische Werte gegeben sind. Um auf das gestufte F&E-Projektbeispiel am Anfang zurückzukommen, wird die Erfolgswahrscheinlichkeit in jeder Phase als binäre diskrete Verteilung modelliert, wobei ein Ergebnis von 1 Erfolg und 0 Misserfolg darstellt.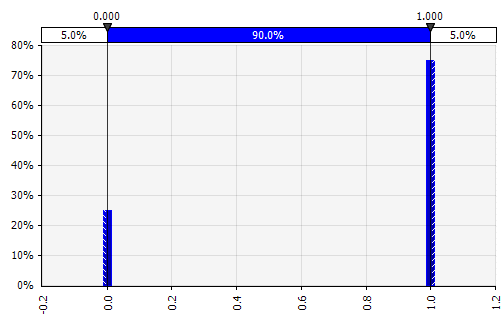
Verteilerarmatur. Wenn Sie über eine große Menge historischer Datenpunkte verfügen, ist die Verteilungsanpassungsfunktion nützlich. Dies bedeutet beispielsweise nicht drei oder vier Jahre historisches Umsatzwachstum, sondern Zeitreihendaten wie Rohstoffpreise, Wechselkurse oder andere Marktpreise, bei denen die Historie nützliche Informationen über zukünftige Trends und den Grad der Unsicherheit liefern kann.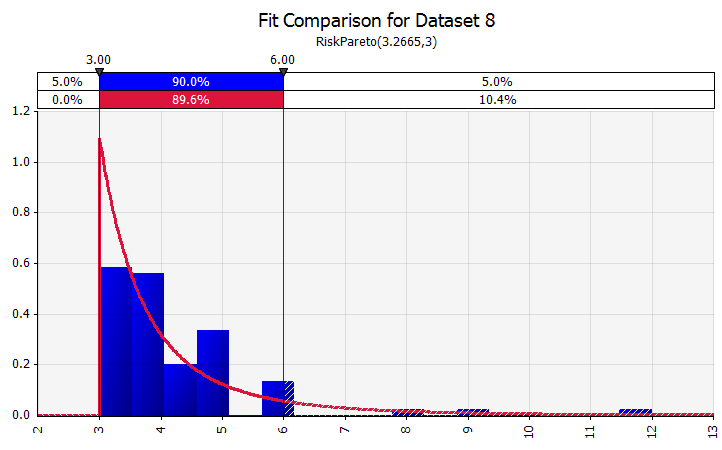
Kombinieren mehrerer verschiedener Distributionen zu einer. Um die potenziellen Auswirkungen individueller Vorurteile abzumildern, ist es oft eine gute Idee, den Input verschiedener Quellen in eine Annahme einzubeziehen und/oder die Ergebnisse zu überprüfen und zu diskutieren. Es gibt verschiedene Ansätze: 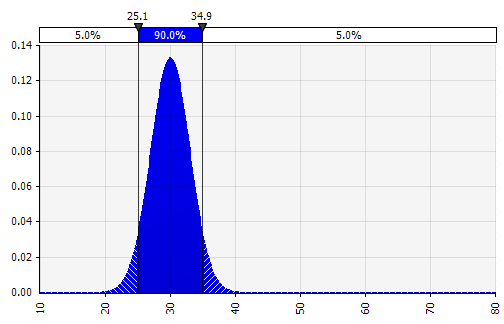Erstellen Sie einen Entwurf oder eine erste Ansicht und überprüfen Sie diese dann mit Experten, dem breiteren Managementteam oder anderen Entscheidungsträgern. Erarbeiten Sie gemeinsam in einem Meeting die wichtigsten Distributionen. Dies kann zu einer guten Diskussion und besseren Ergebnissen führen, aber wie immer ist die Zusammensetzung der Gruppe entscheidend; Die Vertretung verschiedener Perspektiven/Funktionen und die Förderung einer Atmosphäre lebhafter, aber respektvoller Debatten sind natürlich hilfreich. Entwickeln Sie eine Verteilung für jede Schlüsselquelle und kombinieren Sie sie, gewichtet danach, wie viel Vertrauen Sie in jede haben. Wenn Sie Input von mehreren verschiedenen Experten erhalten, kann es eine gute Idee sein, jeden von ihnen unabhängig von den anderen seine eigene Meinung äußern zu lassen und sich dann zu einer zusammenzufügen. Die @RISK-Funktion MakeRiskInput erledigt dies für uns.	Gewicht: 20% 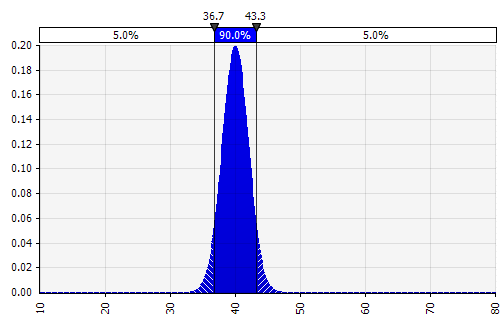+ Gewicht: 20% 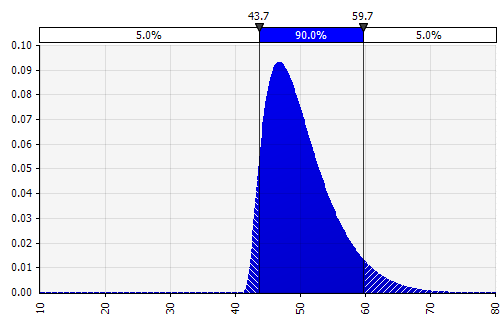+ Gewicht: 60 % =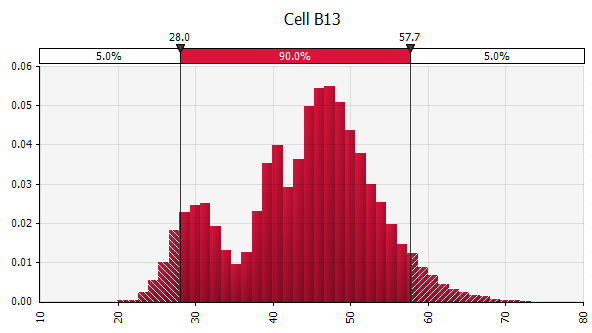
Freihändig. Um eine Verteilung im Rahmen von Diskussionen schnell zu veranschaulichen oder wenn Sie eine Verteilung benötigen, wenn Sie ein Modell entwerfen, das nicht einfach aus der vorhandenen Palette erstellt werden kann, ist die Freihandfunktion nützlich. Wie der Name schon sagt, können Sie die Verteilung mit einem einfachen Malwerkzeug zeichnen.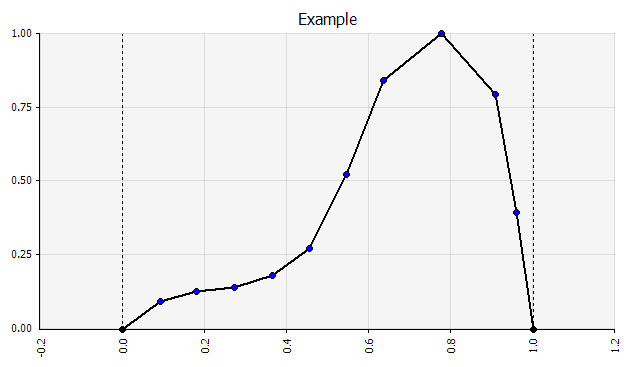

Nun sehen wir eine Visualisierung der Verteilung mit einigen Parametern auf der linken Seite. Die Symbole für Mittelwert und Standardabweichung sollten Ihnen bekannt vorkommen. Bei einer Normalverteilung wäre der Mittelwert das, was wir vorher als Einzelwert in die Zelle eingetragen haben. Hier ist als Beispiel die Verkaufswahrscheinlichkeitsverteilung 2018, wobei 10 % den Mittelwert darstellen. Während sich Ihr typisches Modell entweder nur auf die 10 %-Zahl konzentriert oder „bullen“- und „bären“-Szenarien mit vielleicht 15 % bzw. 5 % Wachstum hat, liefert dies nun Informationen über die gesamte Bandbreite der erwarteten potenziellen Ergebnisse.

Ein Vorteil von Monte-Carlo-Simulationen besteht darin, dass Tail-Ergebnisse mit geringer Wahrscheinlichkeit zum Nachdenken und zu Diskussionen führen können. Nur die Darstellung von Aufwärts- und Abwärtsszenarien kann das Risiko bergen, dass Entscheidungsträger diese als äußere Grenzen interpretieren und alle außerhalb liegenden Szenarien verwerfen. Dies kann zu einer fehlerhaften Entscheidungsfindung führen, mit Ergebnissen, die außerhalb der Risikotoleranz der Organisation oder des Einzelnen liegen. Selbst eine Wahrscheinlichkeit von 5 % oder 1 % kann inakzeptabel sein, wenn das betreffende Szenario katastrophale Folgen hätte.

Schritt 3. Erweiterung der Umsatzprognose von einem Jahr auf mehrere

Achten Sie bei der Monte-Carlo-Modellierung darauf, wie sich Unsicherheits- und Wahrscheinlichkeitsverteilungen überlagern, z. B. im Laufe der Zeit. Sehen wir uns ein Beispiel an. Da der Umsatz in jedem Jahr vom Wachstum in den vorangegangenen Jahren abhängt, können wir uns vorstellen und sehen, dass unsere Schätzung des Umsatzes für 2022 unsicherer ist als die für 2018 (dargestellt anhand der Standardabweichungen und 95-%-Konfidenzintervalle in jedem Jahr). Der Einfachheit halber gibt das folgende Beispiel das Wachstum für ein Jahr, 2018, an und wendet dann dieselbe Wachstumsrate auf jedes der folgenden Jahre bis 2022 an. Ein anderer Ansatz besteht darin, fünf unabhängige Verteilungen zu haben, eine für jedes Jahr.

Schritt 4. Weiter nach unten in der Gewinn- und Verlustrechnung – Margen als Wahrscheinlichkeitsverteilungen ausdrücken

Wir schätzen nun eine Wahrscheinlichkeitsverteilung für die EBIT-Marge im Jahr 2018 (unten hervorgehoben) ähnlich wie wir es für das Umsatzwachstum getan haben.

Hier können wir die Korrelationsfunktion verwenden, um eine Situation zu simulieren, in der es eine klare Korrelation zwischen relativem Marktanteil und Rentabilität gibt, was Skaleneffekte widerspiegelt. Szenarien mit höherem Umsatzwachstum relativ zum Markt und entsprechend höherem relativen Marktanteil können so modelliert werden, dass sie eine positive Korrelation mit höheren EBIT-Margen aufweisen. In Branchen, in denen das Vermögen eines Unternehmens stark mit anderen externen Faktoren wie Ölpreisen oder Wechselkursen korreliert, kann es sinnvoll sein, eine Verteilung für diesen Faktor zu definieren und eine Korrelation mit Umsatz und Rentabilität zu modellieren.

Abhängig von der verfügbaren Zeit, der Transaktionsgröße und anderen Faktoren ist es oft sinnvoll, ein Betriebsmodell zu erstellen und die unsichersten Variablen explizit einzugeben. Dazu gehören: Produktvolumen und -preise, Rohstoffpreise, Wechselkurse, wichtige Gemeinkostenposten, monatlich aktive Benutzer und durchschnittlicher Umsatz pro Einheit (ARPU). Es ist auch möglich, über Mengenvariablen wie Entwicklungszeit, Time-to-Market oder Markteinführungsrate hinaus zu modellieren.

Schritt 5. Bilanz und Kapitalflussrechnung

Unter Verwendung des skizzierten Ansatzes können wir nun mit der Bilanz und der Kapitalflussrechnung fortfahren, Annahmen füllen und Wahrscheinlichkeitsverteilungen verwenden, wo es sinnvoll ist.

Ein Hinweis zu Investitionsausgaben: Diese können entweder in absoluten Beträgen oder als Prozentsatz des Umsatzes modelliert werden, möglicherweise in Kombination mit größeren schrittweisen Investitionen; Eine Produktionsstätte kann beispielsweise eine klare Kapazitätsgrenze haben und eine große Erweiterungsinvestition oder eine neue Anlage erforderlich sein, wenn der Umsatz die Schwelle überschreitet. Da jede der sagen wir 1.000 oder 10.000 Iterationen eine vollständige Neuberechnung des Modells darstellt, kann eine einfache Formel verwendet werden, die die Investitionskosten auslöst, wenn/wenn ein bestimmtes Volumen erreicht wird.

Schritt 6. Finalisieren des Modells

Die Erstellung eines Monte-Carlo-Modells hat im Vergleich zu einem Standard-Finanzmodell einen zusätzlichen Schritt: Die Zellen, in denen wir die Ergebnisse auswerten möchten, müssen ausdrücklich als Ausgabezellen gekennzeichnet werden. Die Software speichert die Ergebnisse jeder Iteration der Simulation für diese Zellen, damit wir sie nach Abschluss der Simulation auswerten können. Alle Zellen im gesamten Modell werden bei jeder Iteration neu berechnet, aber die Ergebnisse der Iterationen in anderen Zellen, die nicht als Eingabe- oder Ausgabezellen gekennzeichnet sind, gehen verloren und können nach Abschluss der Simulation nicht analysiert werden. Wie Sie im folgenden Screenshot sehen können, weisen wir die MIRR-Ergebniszelle als Ausgabezelle aus.

Wenn Sie mit dem Bau des Modells fertig sind, ist es an der Zeit, die Simulation zum ersten Mal auszuführen, indem Sie einfach auf „Simulation starten“ drücken und einige Sekunden warten.

Schritt 7. Interpretieren der Ergebnisse

Ausgaben ausgedrückt als Wahrscheinlichkeiten. Während unser Modell uns zuvor einen einzigen Wert für den modifizierten IRR lieferte, können wir jetzt klar erkennen, dass es um diesen Wert herum eine Reihe potenzieller Ergebnisse mit unterschiedlichen Wahrscheinlichkeiten gibt. Dies ermöglicht es uns, Fragen neu zu formulieren, wie z. B. „Werden wir mit dieser Investition unsere Renditehürde erreichen?“ zu „Wie wahrscheinlich ist es, dass wir unsere Hurdle Rate erreichen oder überschreiten?“ Sie können untersuchen, welche Ergebnisse am wahrscheinlichsten sind, indem Sie beispielsweise ein Konfidenzintervall verwenden. Die Visualisierung ist hilfreich, wenn Sie die Ergebnisse an verschiedene Stakeholder kommunizieren, und Sie können die Ergebnisse anderer Transaktionen überlagern, um visuell zu vergleichen, wie attraktiv und (un)sicher die aktuelle im Vergleich zu anderen ist (siehe unten).

Den Grad der Unsicherheit im Endergebnis verstehen. Wenn wir ein Diagramm der Cashflow-Variabilität im Laufe der Zeit erstellen, ähnlich wie wir es ursprünglich für den Umsatz gemacht haben, wird deutlich, dass die Variabilität des freien Cashflows selbst bei relativ bescheidener Ungewissheit beim Umsatz und den anderen Eingaben, die wir als Wahrscheinlichkeitsverteilungen modelliert haben, signifikant wird , mit Ergebnissen von rund 0,5 Mio. € bis 5,0 Mio. € – ein Faktor von 10x – sogar nur eine Standardabweichung vom Mittelwert. Dies ist das Ergebnis der Übereinanderstapelung unsicherer Annahmen, ein Effekt, der sich sowohl „vertikal“ über die Jahre als auch „horizontal“ durch den Jahresabschluss hindurch verstärkt. Die Visualisierungen geben Auskunft über beide Unsicherheitsarten.

Sensitivitätsanalyse: Einführung in den Tornado-Graphen. Ein weiterer wichtiger Bereich ist zu verstehen, welche Eingaben den größten Einfluss auf Ihr Endergebnis haben. Ein klassisches Beispiel ist, dass der Bedeutung von Diskontsatz- oder Endwertannahmen im Vergleich zu Cashflow-Prognosen oft zu wenig Gewicht beigemessen wird. Eine gängige Methode, dies zu handhaben, ist die Verwendung von Matrizen, bei denen Sie eine Schlüsseleingabe auf jeder Achse platzieren und dann das Ergebnis in jeder Zelle berechnen (siehe unten). Dies ist besonders in Situationen nützlich, in denen Entscheidungen von einer oder wenigen Schlüsselannahmen abhängen – in diesen „was man glauben muss“-Situationen können Entscheidungsträger in (zum Beispiel) einem Anlageausschuss oder einem Senior Management Team unterschiedliche Ansichten haben diese Schlüsselannahmen, und eine Matrix wie die obige ermöglicht es jedem von ihnen, einen Ergebniswert zu finden, der seiner Ansicht entspricht, und kann auf dieser Grundlage entscheiden, abstimmen oder Ratschläge erteilen.

Verbesserung mit Monte-Carlo-Simulationen. Bei der Verwendung von Monte-Carlo-Simulationen kann dieser Ansatz durch einen weiteren ergänzt werden: das Tornado-Diagramm. Diese Visualisierung listet die verschiedenen unsicheren Eingaben und Annahmen auf der vertikalen Achse auf und zeigt dann, wie groß der Einfluss jeder einzelnen auf das Endergebnis ist.

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein