Boîte à outils du prévisionniste : comment effectuer des simulations de Monte-Carlo

Résumé

introduction

Premièrement, la seule certitude est qu'il n'y a pas de certitude. Deuxièmement, chaque décision en conséquence est une question de pesée des probabilités. Troisièmement, malgré l'incertitude, nous devons décider et nous devons agir. Et enfin, nous devons juger les décisions non seulement sur les résultats, mais sur la manière dont ces décisions ont été prises. – Robert E. Rubin

L'un des aspects les plus importants et les plus difficiles de la prévision est la gestion de l'incertitude inhérente à l'examen de l'avenir. Ayant construit et rempli des centaines de modèles financiers et opérationnels pour les LBO, les levées de fonds de démarrage, les budgets, les fusions et acquisitions et les plans stratégiques d'entreprise depuis 2003, j'ai été témoin d'un large éventail d'approches pour y parvenir. Chaque PDG, directeur financier, membre du conseil d'administration, investisseur ou membre du comité d'investissement apporte sa propre expérience et sa propre approche des projections financières et de l'incertitude, influencées par différentes incitations. Souvent, la comparaison des résultats réels avec les projections permet d'apprécier l'ampleur des écarts entre les prévisions et les résultats réels, et donc la nécessité de comprendre et de reconnaître explicitement l'incertitude.

J'ai commencé par utiliser des analyses de scénarios et de sensibilité pour modéliser l'incertitude, et je les considère toujours comme des outils très utiles. Depuis que j'ai ajouté les simulations de Monte Carlo à ma boîte à outils en 2010, j'ai trouvé qu'elles étaient un outil extrêmement efficace pour affiner et améliorer votre façon de penser au risque et aux probabilités. J'ai utilisé l'approche pour tout, depuis la construction d'évaluations DCF, l'évaluation des options d'achat dans les fusions et acquisitions, et la discussion des risques avec les prêteurs jusqu'à la recherche de financement et l'orientation de l'allocation des fonds de capital-risque pour les startups. L'approche a toujours été bien accueillie par les membres du conseil d'administration, les investisseurs et les équipes de direction. Dans cet article, je propose un didacticiel étape par étape sur l'utilisation pratique des simulations de Monte Carlo en créant un modèle d'évaluation DCF.

Chaque décision est une question de probabilités

Avant de commencer avec l'étude de cas, passons en revue quelques approches différentes pour gérer l'incertitude. Le concept de valeur attendue - la moyenne pondérée par les probabilités des flux de trésorerie dans tous les scénarios possibles - est Finance 101. Mais les professionnels de la finance, et les décideurs plus largement, adoptent des approches très différentes lorsqu'ils traduisent cette simple idée en pratique. L'approche peut aller de la simple absence de reconnaissance ou de discussion de l'incertitude, d'une part, à des modèles et logiciels sophistiqués, d'autre part. Dans certains cas, les gens finissent par passer plus de temps à discuter des probabilités qu'à calculer les flux de trésorerie.

En plus de simplement ne pas l'aborder, examinons quelques façons de gérer l'incertitude dans les projections à moyen ou long terme. Beaucoup d'entre eux devraient vous être familiers.

Création d'un scénario. Cette approche est la valeur par défaut pour les budgets, de nombreuses startups et même les décisions d'investissement. En plus de ne contenir aucune information sur le degré d'incertitude ou de reconnaître que les résultats peuvent différer des projections, il peut être ambigu et être interprété différemment selon la partie prenante. Certains peuvent l'interpréter comme une cible extensible, où le résultat réel est plus susceptible d'être en deçà que de dépasser. Certains y voient une performance de base avec plus d'avantages que d'inconvénients. D'autres peuvent le voir comme un "cas de base" avec une probabilité de 50/50 de haut en bas. Dans certaines approches, en particulier pour les startups, il est très ambitieux et l'échec ou le manque à gagner est de loin le résultat le plus probable, mais un taux d'actualisation plus élevé est utilisé pour tenter de tenir compte du risque.	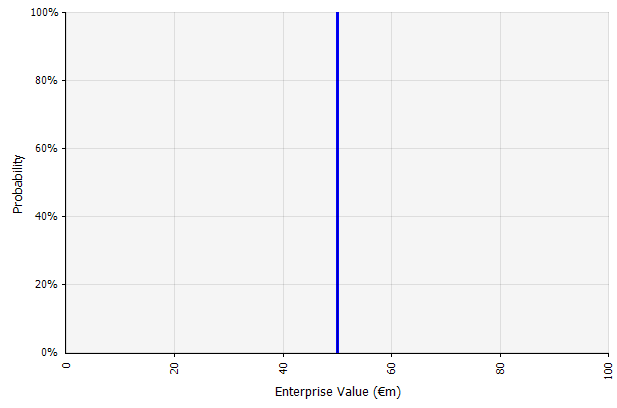Les entrées dans les prévisions de flux de trésorerie à long terme selon cette approche sont toutes des estimations ponctuelles, ce qui donne un résultat d'estimation ponctuelle de 50 millions d'euros dans cet exemple, avec une probabilité implicite de 100 %.
Création de plusieurs scénarios. Cette approche reconnaît qu'il est peu probable que la réalité se déroule selon un seul plan donné. 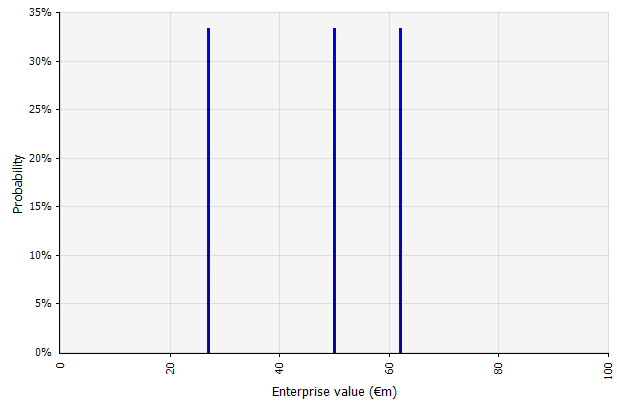Dans sa forme la plus simple, l'analyse de sensibilité, cela pourrait simuler l'impact, par exemple, d'une croissance des ventes de 10 % supérieure et inférieure à celle du scénario de base, en utilisant une combinaison donnée de coûts fixes, semi-variables et variables pour estimer le résultat net impacter. Dans des formes plus complexes, vous pensez à l'avenir d'un point de vue complètement différent pour chaque scénario et analysez l'impact que les différents développements technologiques, la dynamique concurrentielle et les tendances macro auront sur les performances de l'entreprise. Souvent, les scénarios sont malheureusement choisis assez arbitrairement, et parfois avec un résultat final souhaité à l'esprit.	Les trois scénarios différents donnent trois résultats différents, supposés ici équiprobables. Les probabilités de résultats en dehors des scénarios haut et bas ne sont pas prises en compte.
Créer des cas de base, à la hausse et à la baisse avec des probabilités explicitement reconnues. Autrement dit, les cas baissier et haussier contiennent, par exemple, une probabilité de 25 % dans chaque queue, et l'estimation de la juste valeur représente le point médian. Un avantage utile de ceci du point de vue de la gestion des risques est l'analyse explicite du risque extrême, c'est-à-dire des événements en dehors des scénarios haussiers et baissiers.	Illustration tirée du manuel d'évaluation Morningstar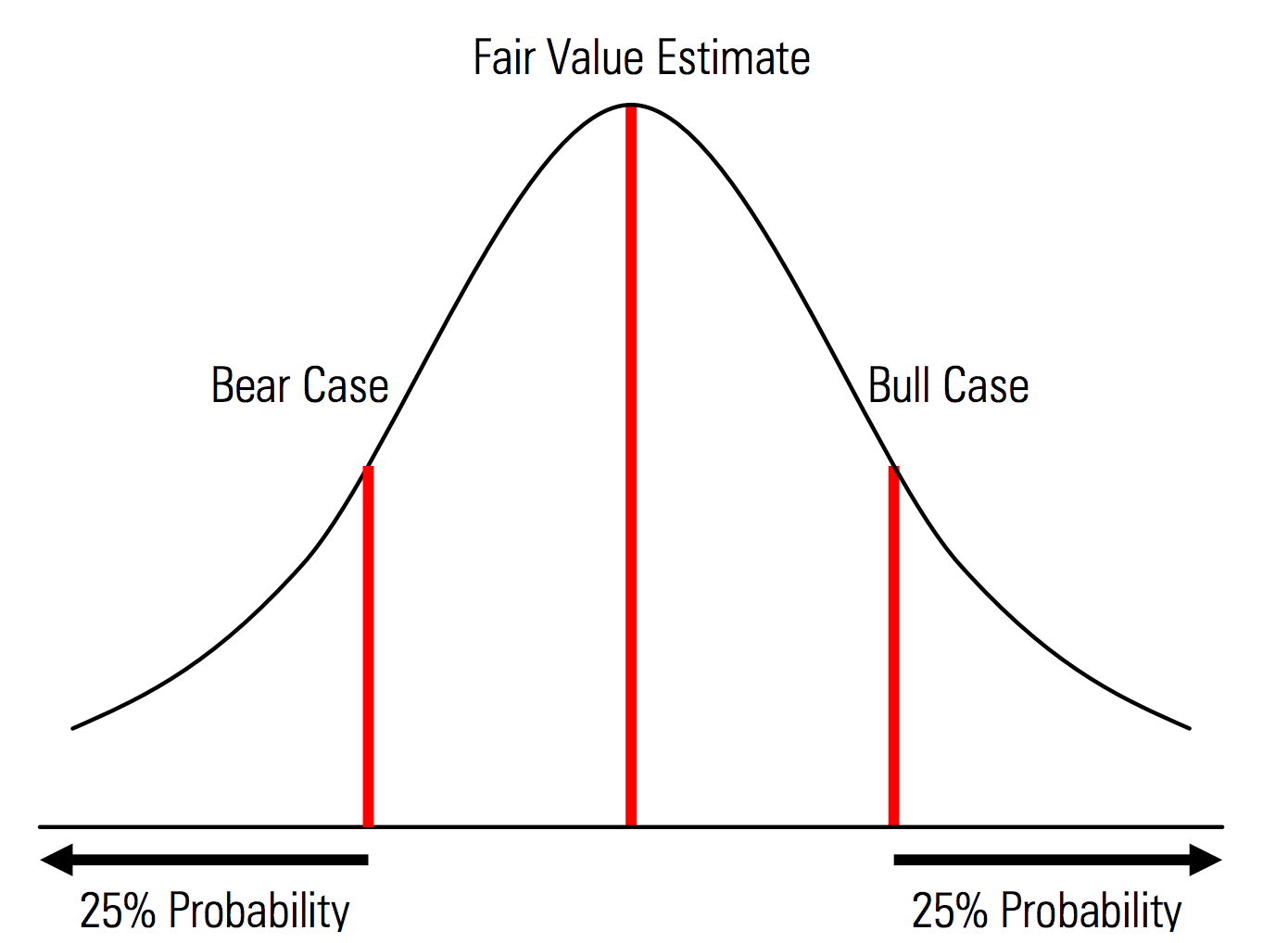
Utilisation de distributions de probabilité et de simulations de Monte Carlo. L'utilisation de distributions de probabilité vous permet de modéliser et de visualiser la gamme complète des résultats possibles dans la prévision. Cela peut être fait non seulement à un niveau agrégé, mais également pour des entrées, des hypothèses et des facteurs individuels détaillés. Les méthodes de Monte Carlo sont ensuite utilisées pour calculer les distributions de probabilité résultantes à un niveau agrégé, permettant l'analyse de la façon dont plusieurs variables incertaines contribuent à l'incertitude des résultats globaux. Peut-être plus important encore, l'approche oblige toutes les personnes impliquées dans l'analyse et la décision à reconnaître explicitement l'incertitude inhérente à la prévision et à penser en probabilités. Tout comme les autres approches, cela a ses inconvénients, y compris le risque de fausse précision et d'excès de confiance qui peut résulter de l'utilisation d'un modèle plus sophistiqué, et le travail supplémentaire requis pour sélectionner des distributions de probabilité appropriées et estimer leurs paramètres là où, autrement, seules des estimations ponctuelles seraient. utilisé.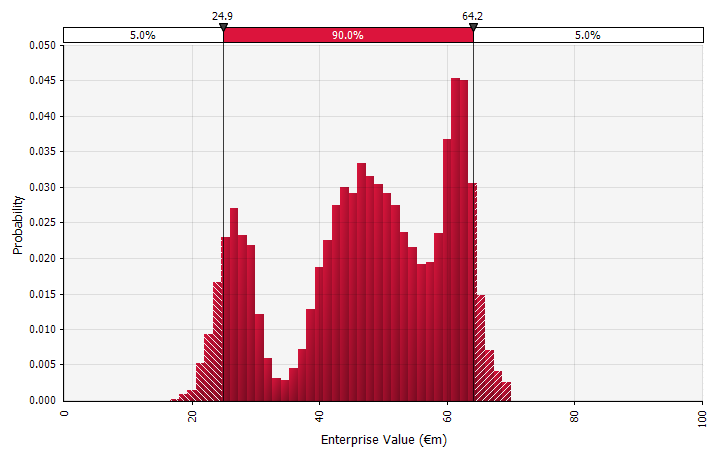

Qu'est-ce qu'une simulation de Monte-Carlo ?

Les simulations de Monte Carlo modélisent la probabilité de différents résultats dans les prévisions et estimations financières. Ils tirent leur nom du quartier de Monte Carlo à Monaco, mondialement connu pour ses casinos haut de gamme ; les résultats aléatoires sont au cœur de la technique, tout comme ils le sont pour la roulette et les machines à sous. Les simulations de Monte Carlo sont utiles dans un large éventail de domaines, notamment l'ingénierie, la gestion de projets, l'exploration pétrolière et gazière et d'autres industries à forte intensité de capital, la R&D et l'assurance ; ici, je me concentre sur les applications en finance et en affaires.

Distributions de probabilité

Dans la simulation, les entrées incertaines sont décrites à l'aide de distributions de probabilité, décrites par des paramètres tels que la moyenne et l'écart type. Des exemples d'entrées dans les projections financières peuvent être n'importe quoi, des revenus et des marges à quelque chose de plus granulaire, comme les prix des matières premières, les dépenses en capital pour une expansion ou les taux de change.

Lorsqu'une ou plusieurs entrées sont décrites comme des distributions de probabilité, la sortie devient également une distribution de probabilité. Un ordinateur tire au hasard un nombre de chaque distribution d'entrée et calcule et enregistre le résultat. Ceci est répété des centaines, des milliers ou des dizaines de milliers de fois, chacune appelée une itération. Lorsqu'elles sont prises ensemble, ces itérations se rapprochent de la distribution de probabilité du résultat final.

Types d'entrées

Les distributions d'entrée peuvent être soit continues , où la valeur générée aléatoirement peut prendre n'importe quelle valeur sous la distribution (par exemple une distribution normale), soit discrètes , où les probabilités sont attachées à deux scénarios distincts ou plus.

Une simulation peut également contenir un mélange de distributions de différents types. Prenons, par exemple, un projet de R&D pharmaceutique comportant plusieurs étapes ayant chacune une probabilité discrète de succès ou d'échec. Cela peut être combiné avec des distributions continues décrivant les montants d'investissement incertains nécessaires pour chaque étape et les revenus potentiels si le projet aboutit à un produit qui atteint le marché. Le graphique ci-dessous montre le résultat d'une telle simulation : une probabilité d'environ 65 % de perdre la totalité de l'investissement de 5 à 50 millions d'euros (valeur actuelle) et une probabilité d'environ 35 % d'un gain net très probablement de l'ordre de 100 € à 250 € : informations qui seraient perdues si des mesures de sortie clés telles que le MIRR ou la VAN étaient présentées sous forme d'estimations ponctuelles plutôt que de distributions de probabilité.

Simulations de Monte Carlo en pratique

L'une des raisons pour lesquelles les simulations de Monte Carlo ne sont pas plus largement utilisées est que les outils financiers quotidiens typiques ne les prennent pas très bien en charge. Excel et Google Sheets contiennent un nombre ou un résultat de formule dans chaque cellule, et bien qu'ils puissent définir des distributions de probabilité et générer des nombres aléatoires, la construction d'un modèle financier avec la fonctionnalité Monte Carlo à partir de zéro est fastidieuse. Et, alors que de nombreuses institutions financières et sociétés d'investissement utilisent des simulations de Monte Carlo pour évaluer les dérivés, analyser les portefeuilles et plus encore, leurs outils sont généralement développés en interne, propriétaires ou d'un coût prohibitif, ce qui les rend inaccessibles au professionnel de la finance individuel.

Ainsi, je souhaite attirer l'attention sur les plugins Excel tels que @RISK de Palisade, ModelRisk de Vose et RiskAMP, qui simplifient grandement le travail avec les simulations Monte Carlo et vous permettent de les intégrer dans vos modèles existants. Dans la procédure pas à pas suivante, j'utiliserai @RISK.

Étude de cas : Projections de flux de trésorerie avec la simulation de Monte Carlo

Passons en revue un exemple simple qui illustre les concepts clés d'une simulation de Monte Carlo : une prévision de flux de trésorerie à cinq ans. Dans cette procédure pas à pas, j'ai configuré et rempli un modèle de flux de trésorerie de base à des fins d'évaluation, remplacé progressivement les entrées par des distributions de probabilité, puis exécuté la simulation et analysé les résultats.

Étape 1. Choisir ou construire le modèle

Pour commencer, j'utilise un modèle simple, axé sur la mise en évidence des principales caractéristiques de l'utilisation des distributions de probabilité. Notez que, pour commencer, ce modèle n'est pas différent de tout autre modèle Excel ; les plugins que j'ai mentionnés ci-dessus fonctionnent avec vos modèles et feuilles de calcul existants. Le modèle ci-dessous est une version standard simple remplie d'hypothèses pour former un scénario.

Étape 2. Création de la première distribution de probabilité

Premièrement, nous devons collecter les informations nécessaires pour faire nos hypothèses, puis nous devons choisir les distributions de probabilité correctes à insérer. Il est important de noter que la source des entrées/hypothèses clés est la même quelle que soit l'approche que vous adoptez pour gérer l'incertitude. La diligence raisonnable commerciale, un examen complet du plan d'affaires de l'entreprise dans le contexte du développement prévu du marché, des tendances de l'industrie et de la dynamique concurrentielle, comprend généralement une extrapolation à partir de données historiques, l'incorporation d'opinions d'experts, la réalisation d'études de marché et des entretiens avec des acteurs du marché. D'après mon expérience, les experts et les acteurs du marché sont heureux de discuter de différents scénarios, risques et gammes de résultats. Cependant, la plupart ne décrivent pas explicitement les distributions de probabilité.

Passons maintenant en revue et remplaçons nos principales valeurs d'entrée par des distributions de probabilité une par une, en commençant par la croissance estimée des ventes pour la première année de prévision (2018). Le plugin @RISK pour Excel peut être évalué avec un essai gratuit de 15 jours afin que vous puissiez le télécharger depuis le site Web de Palisade et l'installer en quelques clics. Avec le plug-in @RISK activé, sélectionnez la cellule dans laquelle vous voulez la distribution et sélectionnez « Définir la distribution » dans le menu.

Vous en sélectionnez ensuite une dans la palette de distributions qui s'affiche. Le logiciel @RISK offre plus de 70 distributions différentes parmi lesquelles choisir, donc en choisir une peut sembler écrasant au premier abord. Vous trouverez ci-dessous un guide pour une poignée que j'utilise le plus souvent :

Normal. Défini par la moyenne et l'écart-type. C'est un bon point de départ en raison de sa simplicité, et adapté comme une extension de l'approche Morningstar, où vous définissez une distribution qui couvre peut-être des scénarios ou des plages déjà définis pour une entrée donnée, en veillant à ce que les cas soient symétriques autour du cas de base et que les probabilités dans chaque queue semblent raisonnables (disons 25 % comme dans l'exemple de Morningstar).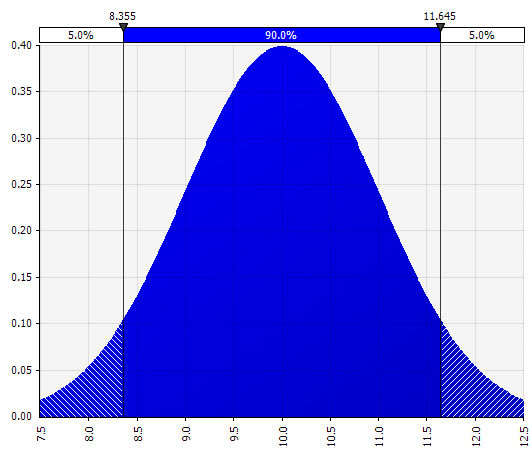
Moments Johnson. Le choix de cette option vous permet de définir des distributions asymétriques et des distributions avec des queues plus grosses ou plus fines (en ajoutant techniquement des paramètres d'asymétrie et d'aplatissement). Dans les coulisses, cela utilise un algorithme pour choisir l'une des quatre distributions qui reflète les quatre paramètres choisis, mais qui est invisible pour l'utilisateur --- tout ce sur quoi nous devons nous concentrer, ce sont les paramètres. Parfois, lors du processus de collecte d'informations pour l'entrée, il devient clair que la distribution normale n'est pas appropriée. Par exemple, pour une entreprise au creux ou au sommet d'un cycle industriel, les probabilités de meilleures ou de moins bonnes performances au cours des, disons, cinq prochaines années ne seront pas symétriques. Plus le pic est proche, plus un ralentissement est probable par rapport à une performance solide et continue. C'est là qu'une distribution asymétrique peut être utile. Beaucoup a été écrit sur le concept de "fat tails" dans de nombreux domaines de la finance. Il semble que la distribution normale ne décrive souvent pas très bien les résultats réels, des événements qui devraient être très rares se produisant plus fréquemment qu'une distribution normale ne l'indiquerait.
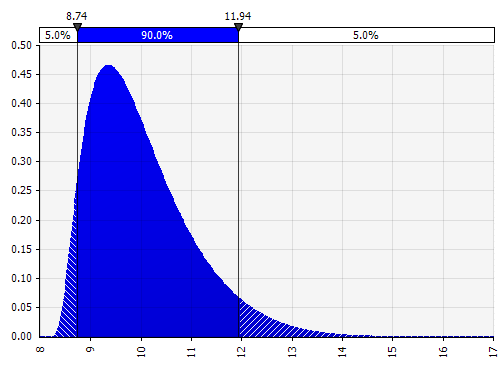Discret. Où les probabilités sont données à deux ou plusieurs valeurs spécifiques. Revenant à l'exemple du projet de R&D par étapes au début, la probabilité de succès à chaque étape est modélisée sous la forme d'une distribution discrète binaire, avec un résultat de 1 représentant le succès et 0 échec.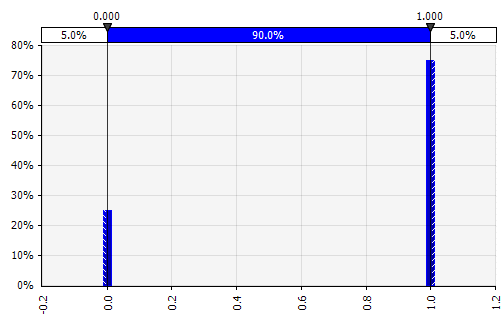
Raccord de distribution. Lorsque vous disposez d'un grand nombre de points de données historiques, la fonctionnalité d'ajustement de distribution est utile. Cela ne signifie pas trois ou quatre ans de croissance historique des ventes, par exemple, mais des données de séries chronologiques telles que les prix des matières premières, les taux de change ou d'autres prix du marché où l'histoire peut fournir des informations utiles sur les tendances futures et le degré d'incertitude.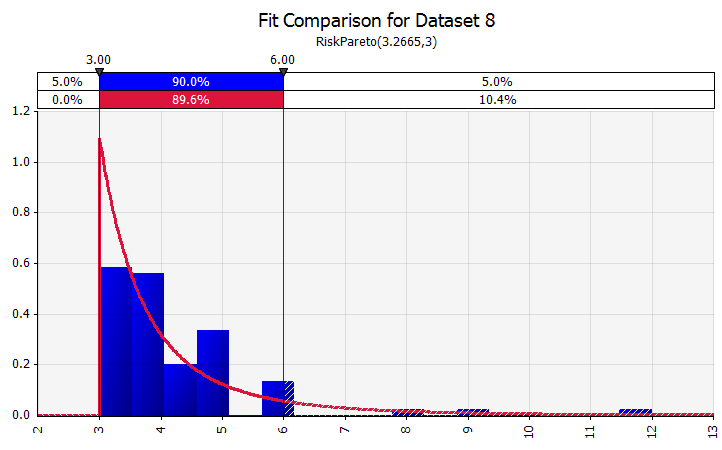
Combiner plusieurs distributions différentes en une seule. Pour atténuer l'impact potentiel des biais individuels, il est souvent judicieux d'intégrer les apports de différentes sources dans une hypothèse et/ou d'examiner et de discuter des résultats. Il existe différentes approches : 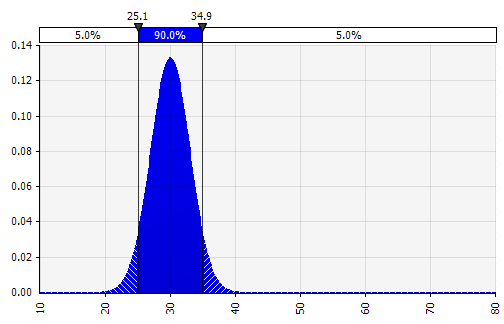Préparez une ébauche ou une première vue, puis examinez-la avec des experts, l'équipe de direction élargie ou d'autres décideurs. Développez les distributions les plus importantes ensemble lors d'une réunion. Cela peut conduire à une bonne discussion et à de meilleurs résultats, mais comme toujours, la composition du groupe est essentielle ; la représentation de différentes perspectives/fonctions et la promotion d'une atmosphère de débat vigoureux mais respectueux sont bien sûr utiles. Développez une distribution pour chaque source clé et combinez-les, pondérées en fonction de la confiance que vous accordez à chacune. Si vous obtenez la contribution de plusieurs experts différents, il peut être judicieux de laisser chacun d'eux donner son propre point de vue, indépendamment des autres, puis de les combiner en un seul. La fonction @RISK MakeRiskInput le fait pour nous.	Poids : 20 % 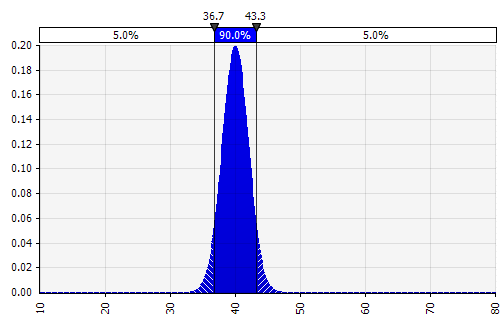+ Poids : 20 % 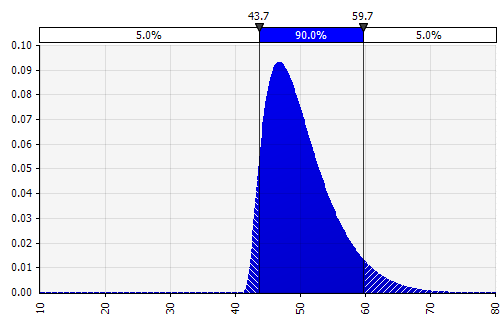+ Poids : 60 % =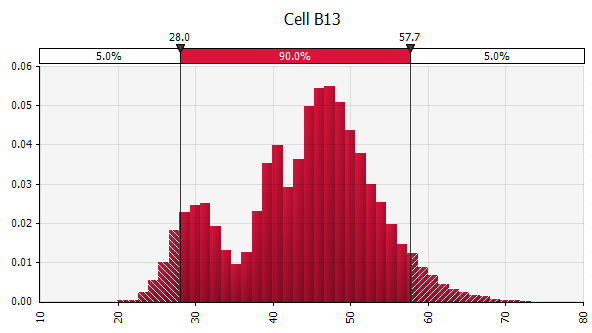
À main levée. Pour illustrer rapidement une distribution dans le cadre de discussions ou si vous avez besoin d'une distribution lors de la rédaction d'un modèle difficile à créer à partir de la palette existante, la fonctionnalité à main levée est utile. Comme son nom l'indique, cela vous permet de dessiner la distribution à l'aide d'un simple outil de peinture.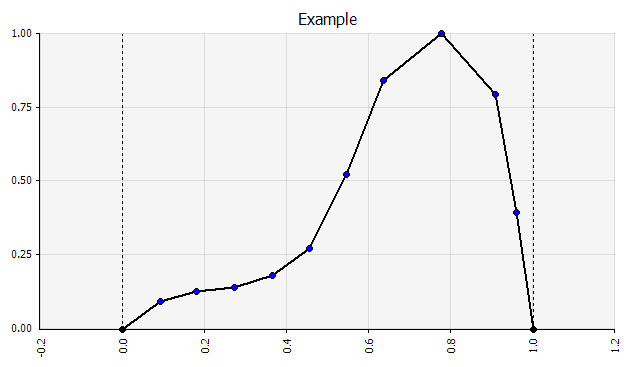

Nous voyons maintenant une visualisation de la distribution, avec quelques paramètres sur le côté gauche. Les symboles de moyenne et d'écart type doivent vous sembler familiers. Dans le cas d'une distribution normale, la moyenne serait ce que nous avons précédemment entré comme valeur unique dans la cellule. Voici la distribution de probabilité des ventes de 2018 à titre d'exemple, 10 % représentant la moyenne. Alors que votre modèle typique se concentrerait uniquement sur le chiffre de 10 % ou aurait des scénarios « haussier » et « baissier » avec peut-être 15 % et 5 % de croissance respectivement, cela fournit désormais des informations sur la gamme complète des résultats potentiels attendus.

L'un des avantages des simulations de Monte Carlo est que les résultats extrêmes à faible probabilité peuvent déclencher des réflexions et des discussions. Seul l'affichage de scénarios à la hausse et à la baisse peut introduire le risque que les décideurs les interprètent comme des limites extérieures, rejetant tous les scénarios qui se trouvent à l'extérieur. Cela peut entraîner une prise de décision erronée, avec une exposition à des résultats qui dépassent la tolérance au risque de l'organisation ou de l'individu. Même une probabilité de 5% ou 1% peut être inacceptable si le scénario en question aurait des conséquences catastrophiques.

Étape 3. Extension des prévisions de revenus d'un an à plusieurs

Avec la modélisation de Monte Carlo, gardez à l'esprit la façon dont les distributions d'incertitude et de probabilité s'empilent les unes sur les autres, par exemple au fil du temps. Reprenons un exemple. Étant donné que les ventes de chaque année dépendent de la croissance des années précédentes, nous pouvons visualiser et voir que notre estimation des ventes de 2022 est plus incertaine que celle de 2018 (indiquée en utilisant les écarts-types et les intervalles de confiance à 95 % chaque année). Par souci de simplicité, l'exemple ci-dessous spécifie la croissance pour une année, 2018, puis applique ce même taux de croissance à chacune des années suivantes jusqu'en 2022. Une autre approche consiste à avoir cinq distributions indépendantes, une pour chaque année.

Étape 4. Continuer vers le bas dans le compte de résultat - Exprimer les marges sous forme de distributions de probabilité

Nous estimons maintenant une distribution de probabilité pour la marge EBIT en 2018 (mise en évidence ci-dessous) de la même manière que nous l'avons fait pour la croissance des ventes.

Ici, nous pouvons utiliser la fonction de corrélation pour simuler une situation où il existe une corrélation claire entre la part de marché relative et la rentabilité, reflétant les économies d'échelle. Les scénarios avec une croissance des ventes plus élevée par rapport au marché et une part de marché relative plus élevée en conséquence peuvent être modélisés pour avoir une corrélation positive avec des marges EBIT plus élevées. Dans les secteurs où la fortune d'une entreprise est fortement corrélée à un autre facteur externe, tel que les prix du pétrole ou les taux de change, il peut être judicieux de définir une distribution pour ce facteur et de modéliser une corrélation avec les ventes et la rentabilité.

En fonction du temps disponible, de la taille de la transaction et d'autres facteurs, il est souvent judicieux de construire un modèle opérationnel et de saisir explicitement les variables les plus incertaines. Ceux-ci incluent : les volumes et les prix des produits, les prix des matières premières, les taux de change, les principaux éléments généraux, les utilisateurs actifs mensuels et le revenu moyen par unité (ARPU). Il est également possible de modéliser des variables au-delà du montant telles que le temps de développement, le délai de mise sur le marché ou le taux d'adoption sur le marché.

Étape 5. Bilan et état des flux de trésorerie

En utilisant l'approche décrite, nous pouvons maintenant continuer à travers le bilan et l'état des flux de trésorerie, en remplissant d'hypothèses et en utilisant des distributions de probabilité là où cela a du sens.

Remarque sur les dépenses d'investissement : elles peuvent être modélisées soit en montants absolus, soit en pourcentage des ventes, éventuellement en combinaison avec des investissements progressifs plus importants ; une installation de fabrication peut par exemple avoir une limite de capacité claire et un investissement d'expansion important ou une nouvelle installation nécessaire lorsque les ventes dépassent le seuil. Étant donné que chacune des 1 000 ou 10 000 itérations sera un recalcul complet du modèle, une formule simple qui déclenche le coût d'investissement si/quand un certain volume est atteint peut être utilisée.

Étape 6. Finalisation du modèle

La construction d'un modèle Monte Carlo comporte une étape supplémentaire par rapport à un modèle financier standard : les cellules dont nous voulons évaluer les résultats doivent être spécifiquement désignées comme cellules de sortie. Le logiciel enregistrera les résultats de chaque itération de la simulation pour ces cellules afin que nous les évaluions une fois la simulation terminée. Toutes les cellules du modèle entier sont recalculées à chaque itération, mais les résultats des itérations dans d'autres cellules, qui ne sont pas désignées comme cellules d'entrée ou de sortie, sont perdus et ne peuvent pas être analysés une fois la simulation terminée. Comme vous pouvez le voir dans la capture d'écran ci-dessous, nous désignons la cellule de résultat MIRR comme une cellule de sortie.

Une fois que vous avez fini de construire le modèle, il est temps de lancer la simulation pour la première fois en appuyant simplement sur "démarrer la simulation" et en attendant quelques secondes.

Étape 7. Interprétation des résultats

Sorties exprimées sous forme de probabilités. Alors que notre modèle nous donnait auparavant une valeur unique pour le TRI modifié, nous pouvons maintenant voir clairement qu'il existe un certain nombre de résultats potentiels autour de cette valeur, avec différentes probabilités. Cela nous permet de reformuler des questions telles que « Atteindrons-nous notre taux de rendement minimal avec cet investissement ? » à « Quelle est la probabilité que nous atteignions ou dépassions notre taux de rendement minimal ? » Vous pouvez explorer les résultats les plus susceptibles d'utiliser, par exemple, un intervalle de confiance. La visualisation est utile lors de la communication des résultats aux différentes parties prenantes, et vous pouvez superposer les résultats d'autres transactions pour comparer visuellement à quel point la transaction actuelle est attrayante et (in)certaine par rapport aux autres (voir ci-dessous).

Comprendre le degré d'incertitude du résultat final. Si nous générons un graphique de la variabilité des flux de trésorerie dans le temps, similaire à ce que nous avons fait initialement pour les ventes, il devient clair que la variabilité des flux de trésorerie disponibles devient significative même avec une incertitude relativement modeste dans les ventes et les autres entrées que nous avons modélisées comme distributions de probabilité , avec des résultats allant d'environ 0,5 million d'euros à 5,0 millions d'euros, soit un facteur de 10 x, voire un seul écart type par rapport à la moyenne. C'est le résultat de l'empilement d'hypothèses incertaines les unes sur les autres, un effet qui s'aggrave à la fois « verticalement » au fil des ans et « horizontalement » tout au long des états financiers. Les visualisations fournissent des informations sur les deux types d'incertitude.

Analyse de sensibilité : Présentation du graphique tornade. Un autre domaine important est de comprendre quelles entrées ont le plus grand impact sur votre résultat final. Un exemple classique est la manière dont l'importance des hypothèses de taux d'actualisation ou de valeur terminale est souvent trop peu pondérée par rapport aux prévisions de flux de trésorerie. Une façon courante de gérer cela consiste à utiliser des matrices dans lesquelles vous placez une entrée clé sur chaque axe, puis calculez le résultat dans chaque cellule (voir ci-dessous). Ceci est particulièrement utile dans les situations où les décisions dépendent d'une ou de quelques hypothèses clés - dans ces situations de «ce que vous devez croire», les décideurs d'un comité d'investissement ou d'une équipe de direction peuvent avoir des points de vue différents sur ces hypothèses clés, et une matrice telle que celle ci-dessus permet à chacun d'entre eux de trouver une valeur de résultat correspondant à leur point de vue, et peut décider, voter ou donner des conseils en fonction de cela.

Amélioration avec des simulations de Monte Carlo. Lors de l'utilisation de simulations de Monte Carlo, cette approche peut être complétée par une autre : le diagramme de tornade. Cette visualisation répertorie les différentes entrées et hypothèses incertaines sur l'axe vertical, puis montre l'ampleur de l'impact de chacune sur le résultat final.

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein