Набор инструментов прогнозиста: как выполнять моделирование методом Монте-Карло
Опубликовано: 2022-03-11Управляющее резюме
Что такое моделирование Монте-Карло?
- Моделирование Монте-Карло моделирует вероятность различных результатов в прогнозах и оценках. Они получили свое название от района Монте-Карло в Монако, известного своими элитными казино. Случайные результаты играют центральную роль в этой технике, так же как и в рулетке и игровых автоматах. Моделирование методом Монте-Карло полезно в самых разных областях, включая проектирование, управление проектами, разведку нефти и газа и другие капиталоемкие отрасли, НИОКР и страхование. Эта статья посвящена приложениям в области финансов и бизнеса.
- Распределения вероятностей. При моделировании неопределенные входные данные описываются с использованием вероятностных распределений. Когда один или несколько входных данных описываются как распределения вероятностей, выходные данные также становятся распределением вероятностей. Компьютер случайным образом выбирает число из каждого входного распределения, вычисляет и сохраняет результат. Это повторяется сотни или тысячи раз, каждое из которых называется итерацией. В совокупности эти итерации аппроксимируют распределение вероятностей конечного результата.
Учебное пособие по моделированию методом Монте-Карло
- Шаг 1: Выбор или построение модели. Используйте простую модель, ориентированную на выделение ключевых особенностей использования вероятностных распределений. Обратите внимание, что для начала эта модель ничем не отличается от любой другой модели Excel — плагины работают с вашими существующими моделями и электронными таблицами.
- Шаг 2: Создание первого распределения вероятностей. Во-первых, нам нужно собрать информацию, необходимую для наших предположений, затем нам нужно выбрать правильные распределения вероятностей для вставки. Важно отметить, что источник ключевых исходных данных/предположений один и тот же, независимо от того, какой подход вы используете для работы с неопределенностью. Затем вы проходите и заменяете наши ключевые входные значения распределениями вероятностей одно за другим. Далее вы выберете дистрибутив, который хотите использовать (например, обычный).
- Шаг 3: Расширение прогноза доходов с одного года до нескольких. При моделировании методом Монте-Карло помните о том, как распределения неопределенности и вероятности накладываются друг на друга, например, во времени. Другой подход состоит в том, чтобы иметь пять независимых распределений, по одному на каждый год.
- Шаг 4: Выражение маржи как распределения вероятностей. Здесь мы можем использовать функцию корреляции, чтобы смоделировать ситуацию, когда существует четкая корреляция между относительной долей рынка и прибыльностью, отражающая эффект масштаба. И в зависимости от доступного времени, размера транзакции и других факторов часто имеет смысл построить операционную модель и явно ввести наиболее неопределенные переменные. К ним относятся: объемы и цены продуктов, цены на товары, валютные курсы, ключевые статьи накладных расходов, ежемесячные активные пользователи и средний доход на единицу (ARPU). Также возможно моделировать не только количественные переменные, такие как время разработки, время выхода на рынок или скорость принятия рынком.
- Шаг 5: Балансовый отчет и отчет о движении денежных средств. Используя изложенный подход, мы теперь можем продолжить работу с балансовым отчетом и отчетом о движении денежных средств, внося допущения и используя распределения вероятностей там, где это имеет смысл.
- Шаг 6: Завершение модели. Построение модели Монте-Карло имеет один дополнительный шаг по сравнению со стандартной финансовой моделью: ячейки, в которых мы хотим оценить результаты, должны быть специально обозначены как выходные ячейки. Программное обеспечение будет сохранять результаты каждой итерации моделирования для этих ячеек, чтобы мы могли оценить их после завершения моделирования — все ячейки во всей модели пересчитываются с каждой итерацией, но результаты итераций в других ячейках, которые не обозначенные как входные или выходные ячейки, теряются и не могут быть проанализированы после завершения моделирования. После того, как вы закончили построение модели, пришло время запустить симуляцию в первый раз, просто нажав «Начать симуляцию» и подождав несколько секунд.
- Шаг 7: Интерпретация результатов. Теперь мы можем ясно видеть, что существует ряд потенциальных исходов вокруг этого значения с различной вероятностью. Это позволяет нам перефразировать такие вопросы, как «Сможем ли мы достичь нашей пороговой доходности с этими инвестициями?» на «Насколько вероятно, что мы достигнем или превзойдем нашу пороговую скорость?» Вы можете изучить, какие результаты наиболее вероятны, используя, например, доверительный интервал. Визуализация полезна при передаче результатов различным заинтересованным сторонам, и вы можете накладывать результаты других транзакций, чтобы визуально сравнить, насколько привлекательна и (не) определенна текущая транзакция по сравнению с другими.
- Toptal Finance может помочь вам со всеми вашими потребностями в моделировании с нашими экспертами Excel, консультантами по финансовому моделированию, специалистами по оценке и экспертами по финансовому прогнозированию.
Введение
Во-первых, единственная уверенность в том, что уверенности нет. Во-вторых, каждое решение, как следствие, является вопросом взвешивания вероятностей. В-третьих, несмотря на неопределенность, мы должны принять решение и должны действовать. И, наконец, нам нужно судить о решениях не только по результатам, но и по тому, как эти решения были приняты. - Роберт Э. Рубин
Одним из наиболее важных и сложных аспектов прогнозирования является работа с неопределенностью, присущей изучению будущего. Создав и заполнив сотни финансовых и операционных моделей для LBO, сбора средств для стартапов, бюджетов, слияний и поглощений и корпоративных стратегических планов с 2003 года, я стал свидетелем широкого спектра подходов к этому. Каждый генеральный директор, финансовый директор, член совета директоров, инвестор или член инвестиционного комитета привносит свой собственный опыт и подход к финансовым прогнозам и неопределенности — под влиянием различных стимулов. Часто сравнение фактических результатов с прогнозами позволяет оценить, насколько большими могут быть отклонения между прогнозами и фактическими результатами, и, следовательно, необходимость понимания и явного признания неопределенности.
Сначала я начал использовать анализ сценариев и чувствительности для моделирования неопределенности и до сих пор считаю их очень полезными инструментами. С тех пор, как в 2010 году я добавил моделирование Монте-Карло в свой набор инструментов, я обнаружил, что это чрезвычайно эффективный инструмент для уточнения и улучшения ваших представлений о риске и вероятностях. Я использовал этот подход для всего: от расчета DCF, оценки колл-опционов при слияниях и поглощениях и обсуждения рисков с кредиторами до поиска финансирования и управления распределением венчурного финансирования для стартапов. Такой подход всегда хорошо воспринимался членами совета директоров, инвесторами и высшим руководством. В этой статье я предлагаю пошаговое руководство по практическому использованию моделирования Монте-Карло путем построения модели оценки DCF.
Каждое решение — это вопрос взвешивания вероятностей
Прежде чем приступить к рассмотрению примера, давайте рассмотрим несколько различных подходов к работе с неопределенностью. Концепция ожидаемой стоимости — средневзвешенное значение денежных потоков во всех возможных сценариях — это Финансы 101. Но профессионалы в области финансов и лица, принимающие решения в целом, применяют совершенно разные подходы при воплощении этого простого понимания на практике. Подход может варьироваться от простого непризнания или вообще обсуждения неопределенности, с одной стороны, до сложных моделей и программного обеспечения, с другой. В некоторых случаях люди тратят больше времени на обсуждение вероятностей, чем на расчет денежных потоков.
Помимо того, что мы просто не будем его рассматривать, давайте рассмотрим несколько способов работы с неопределенностью в среднесрочных или долгосрочных прогнозах. Многие из них должны быть вам знакомы.
Создание одного сценария. Этот подход используется по умолчанию для бюджетов, многих стартапов и даже инвестиционных решений. Помимо того, что он не содержит никакой информации о степени неопределенности или признания того, что результаты могут отличаться от прогнозов, он может быть неоднозначным и интерпретироваться по-разному в зависимости от заинтересованной стороны. Некоторые могут интерпретировать это как растянутую цель, где фактический результат, скорее всего, не превзойдет, а не превзойдет. Некоторые рассматривают это как базовую производительность с большим количеством положительных сторон, чем отрицательных. Другие могут рассматривать это как «базовый случай» с вероятностью 50/50 вверх и вниз. В некоторых подходах, особенно для стартапов, это очень амбициозно, и неудача или дефицит являются более вероятным результатом, но для учета риска используется более высокая ставка дисконтирования. | 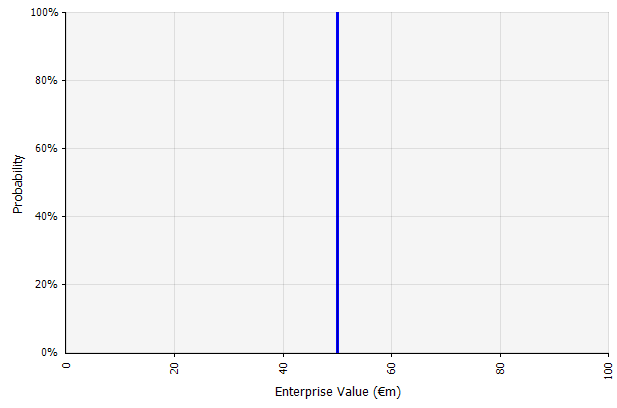 Все входные данные для долгосрочного прогноза движения денежных средств в соответствии с этим подходом представляют собой точечные оценки, что в данном примере дает результат точечной оценки в размере 50 миллионов евро с неявной вероятностью 100%. |
Создание нескольких сценариев. Этот подход признает, что реальность вряд ли будет разворачиваться в соответствии с одним заданным планом.
| 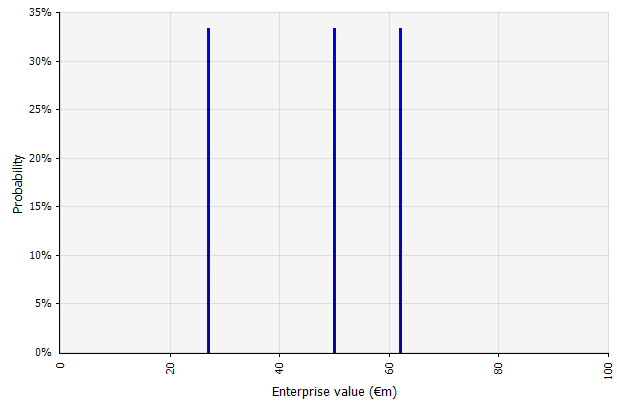 Три разных сценария дают три разных результата, которые здесь считаются равновероятными. Вероятности исходов за пределами высокого и низкого сценариев не учитываются. |
Создание базовых, положительных и отрицательных вариантов с явно распознаваемыми вероятностями. То есть медвежьи и бычьи случаи содержат, например, 25% вероятности в каждом хвосте, а оценка справедливой стоимости представляет собой среднюю точку. Полезным преимуществом этого с точки зрения управления рисками является явный анализ хвостового риска, т. е. событий, выходящих за рамки сценариев роста и падения. | Иллюстрация из Справочника по оценке Morningstar 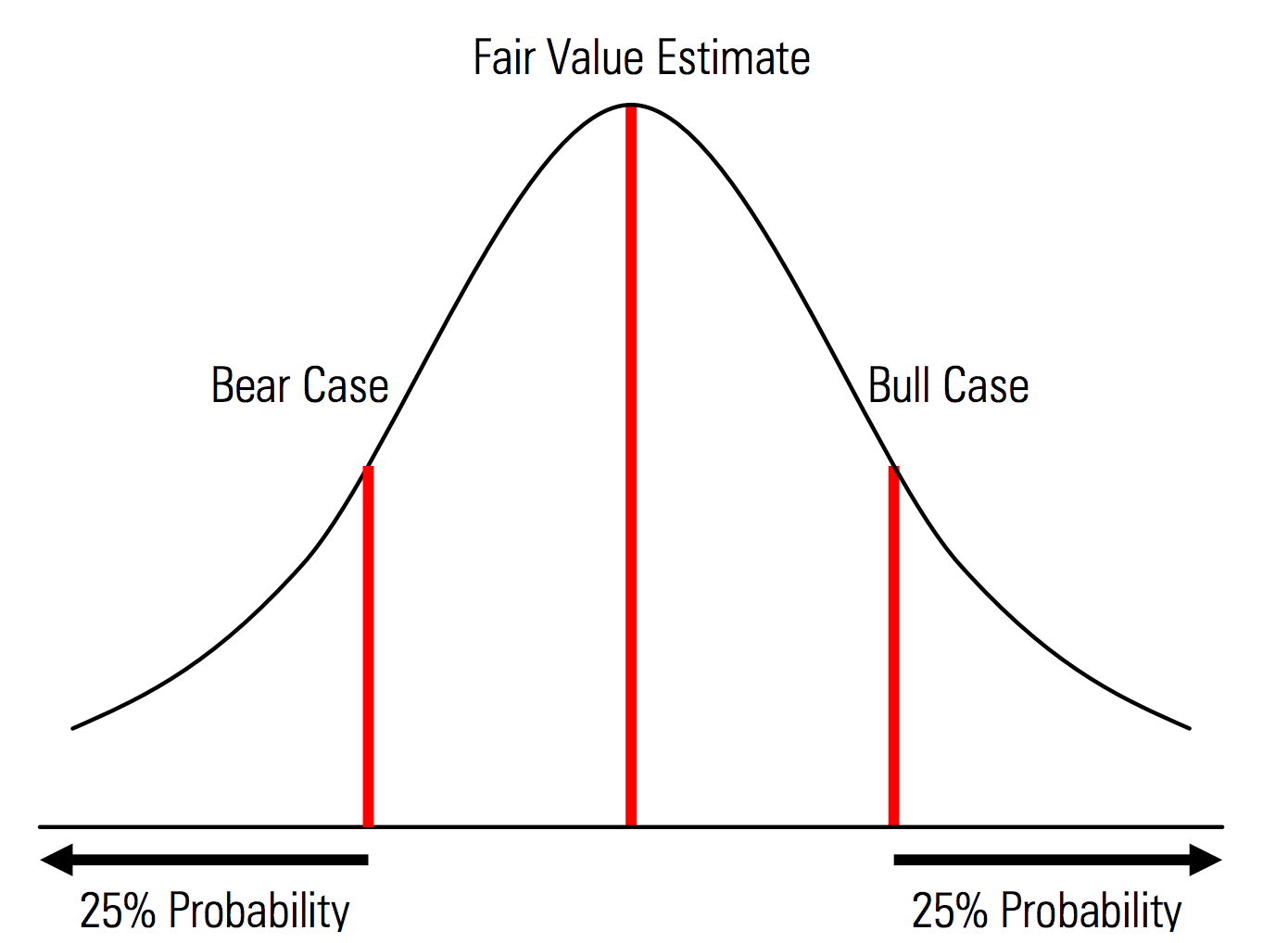 |
Использование распределений вероятностей и моделирования методом Монте-Карло. Использование вероятностных распределений позволяет моделировать и визуализировать весь спектр возможных результатов в прогнозе. Это можно сделать не только на агрегированном уровне, но и для подробных индивидуальных входных данных, допущений и движущих сил. Затем методы Монте-Карло используются для расчета результирующих распределений вероятностей на агрегированном уровне, что позволяет проанализировать, как несколько неопределенных переменных влияют на неопределенность общих результатов. Возможно, наиболее важно то, что этот подход заставляет всех, кто участвует в анализе и принятии решений, четко осознавать неопределенность, присущую прогнозированию, и думать о вероятностях. Как и у других подходов, у этого есть свои недостатки, в том числе риск ложной точности и, как следствие, чрезмерной уверенности, которая может возникнуть при использовании более сложной модели, а также дополнительная работа, необходимая для выбора подходящих распределений вероятностей и оценки их параметров, где в противном случае были бы только точечные оценки. использовал. | 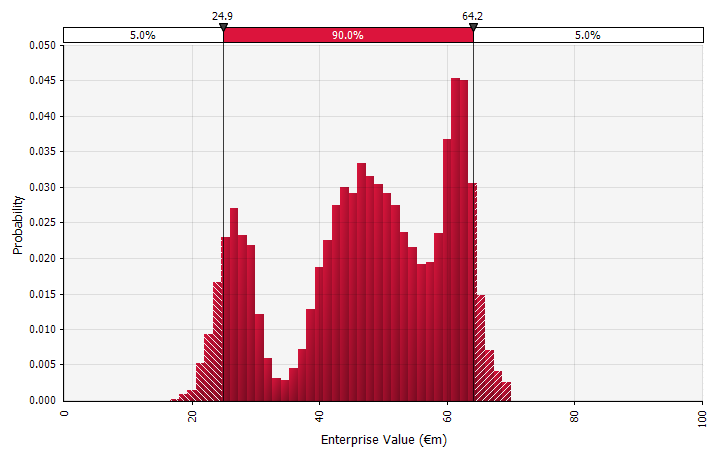 |
Что такое моделирование Монте-Карло?
Моделирование Монте-Карло моделирует вероятность различных результатов в финансовых прогнозах и оценках. Они получили свое название от района Монте-Карло в Монако, который всемирно известен своими элитными казино. случайные исходы играют центральную роль в этой технике, так же как и в рулетке и игровых автоматах. Моделирование методом Монте-Карло полезно в самых разных областях, включая проектирование, управление проектами, разведку нефти и газа и другие капиталоемкие отрасли, НИОКР и страхование; здесь я сосредоточусь на приложениях в области финансов и бизнеса.
Распределения вероятностей
При моделировании неопределенные входные данные описываются с помощью распределений вероятностей, описываемых такими параметрами, как среднее значение и стандартное отклонение. Примером входных данных в финансовых прогнозах может быть что угодно, от выручки и маржи до чего-то более детального, например, цены на товары, капитальные затраты на расширение или обменные курсы.
Когда один или несколько входных данных описываются как распределения вероятностей, выходные данные также становятся распределением вероятностей. Компьютер случайным образом выбирает число из каждого входного распределения, вычисляет и сохраняет результат. Это повторяется сотни, тысячи или десятки тысяч раз, каждое из которых называется итерацией. В совокупности эти итерации аппроксимируют распределение вероятностей конечного результата.
Типы входов
Входные распределения могут быть либо непрерывными , когда случайно сгенерированное значение может принимать любое значение в соответствии с распределением (например, нормальное распределение), либо дискретными , когда вероятности привязаны к двум или более различным сценариям.
Моделирование также может содержать смесь распределений разных типов. Возьмем, к примеру, фармацевтический научно-исследовательский проект с несколькими этапами, каждый из которых имеет дискретную вероятность успеха или неудачи. Это можно комбинировать с непрерывными распределениями, описывающими неопределенные суммы инвестиций, необходимые для каждого этапа, и потенциальные доходы, если в результате проекта будет выпущен продукт, который выйдет на рынок. На приведенной ниже диаграмме показаны результаты такого моделирования: вероятность потери всех инвестиций в размере от 5 до 50 миллионов евро (текущая стоимость) составляет ~65 %, а вероятность чистой прибыли в размере ~35 %, скорее всего, находится в диапазоне От 100 до 250 евро — информация, которая будет потеряна, если ключевые выходные показатели, такие как MIRR или NPV, будут показаны в виде точечных оценок, а не распределений вероятностей.
Моделирование методом Монте-Карло на практике
Одна из причин, по которой моделирование методом Монте-Карло не используется более широко, заключается в том, что типичные повседневные финансовые инструменты не очень хорошо их поддерживают. Таблицы Excel и Google Sheets содержат одно число или результат формулы в каждой ячейке, и хотя они могут определять распределения вероятностей и генерировать случайные числа, построение финансовой модели с помощью функции Монте-Карло с нуля является громоздким. И хотя многие финансовые учреждения и инвестиционные фирмы используют моделирование методом Монте-Карло для оценки деривативов, анализа портфелей и многого другого, их инструменты, как правило, разрабатываются собственными силами, запатентованы или слишком дороги, что делает их недоступными для отдельных специалистов по финансам.
Таким образом, я хочу обратить внимание на плагины Excel, такие как @RISK от Palisade, ModelRisk от Vose и RiskAMP, которые значительно упрощают работу с симуляциями Монте-Карло и позволяют интегрировать их в существующие модели. В следующем пошаговом руководстве я буду использовать @RISK.
Практический пример: прогнозы денежных потоков с помощью моделирования Монте-Карло
Давайте рассмотрим простой пример, иллюстрирующий ключевые концепции моделирования Монте-Карло: пятилетний прогноз движения денежных средств. В этом пошаговом руководстве я настраиваю и заполняю базовую модель денежного потока для целей оценки, постепенно заменяю входные данные вероятностными распределениями и, наконец, запускаю моделирование и анализирую результаты.
Шаг 1. Выбор или построение модели
Для начала я использую простую модель, ориентированную на выделение ключевых особенностей использования вероятностных распределений. Обратите внимание, что для начала эта модель ничем не отличается от любой другой модели Excel; плагины, о которых я упоминал выше, работают с вашими существующими моделями и электронными таблицами. Приведенная ниже модель представляет собой простую готовую версию, заполненную предположениями для формирования одного сценария.
Шаг 2. Создание первого распределения вероятностей
Во-первых, нам нужно собрать информацию, необходимую для наших предположений, затем нам нужно выбрать правильные распределения вероятностей для вставки. Важно отметить, что источник ключевых исходных данных/предположений один и тот же, независимо от того, какой подход вы используете для работы с неопределенностью. Коммерческая экспертиза, всесторонний обзор бизнес-плана компании в контексте прогнозируемого развития рынка, отраслевых тенденций и динамики конкуренции, как правило, включает в себя экстраполяцию исторических данных, учет мнений экспертов, проведение маркетинговых исследований и опрос участников рынка. По моему опыту, эксперты и участники рынка с удовольствием обсуждают разные сценарии, риски и диапазоны результатов. Однако большинство из них явно не описывают распределения вероятностей.
Давайте теперь пройдемся и заменим наши ключевые входные значения распределениями вероятностей одно за другим, начиная с предполагаемого роста продаж для первого прогнозируемого года (2018). Плагин @RISK для Excel можно оценить с помощью 15-дневной бесплатной пробной версии, поэтому вы можете загрузить его с веб-сайта Palisade и установить несколькими щелчками мыши. При включенном плагине @RISK выберите ячейку, в которую вы хотите распределить, и выберите «Определить распределение» в меню.
Затем вы выбираете один из появившейся палитры дистрибутивов. Программное обеспечение @RISK предлагает на выбор более 70 различных дистрибутивов, поэтому поначалу выбор одного из них может показаться ошеломляющим. Ниже приведено руководство по нескольким из них, которые я использую чаще всего:
Обычный. Определяется средним значением и стандартным отклонением. Это хорошая отправная точка из-за своей простоты, и она подходит в качестве расширения подхода Морнингстара, где вы определяете распределение, которое охватывает, возможно, уже определенные сценарии или диапазоны для заданных входных данных, гарантируя, что случаи симметричны относительно базового случая и что вероятности в каждой хвосте выглядят разумными (скажем, 25%, как в примере с Морнингстаром).  | 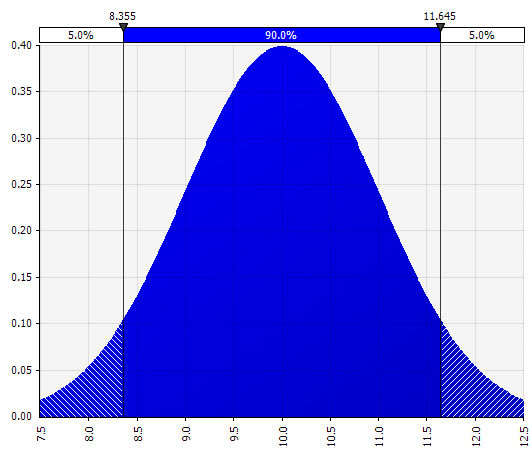 |
Моменты Джонсона. Выбор этого параметра позволяет вам определять асимметричные распределения и распределения с более толстыми или тонкими хвостами (технически добавляя параметры асимметрии и эксцесса). За кулисами используется алгоритм выбора одного из четырех распределений, который отражает четыре выбранных параметра, но невидим для пользователя — все, на чем мы должны сосредоточиться, — это параметры.
| 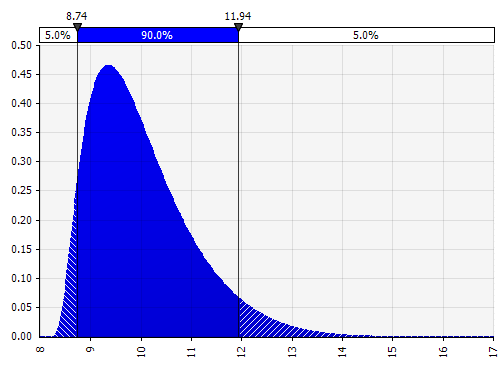 |
Дискретный. Где вероятности даны двум или более конкретным значениям. Возвращаясь к примеру с поэтапным проектом НИОКР в начале, вероятность успеха на каждом этапе моделируется как бинарное дискретное распределение, где результат 1 соответствует успеху, а 0 — неудаче. | 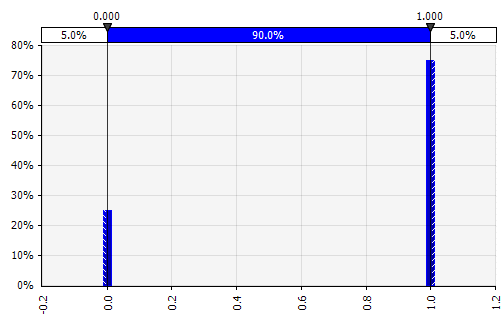 |
Распределительный фитинг. Когда у вас есть большое количество исторических точек данных, полезна функция подгонки распределения. Это не означает, например, три или четыре года исторического роста продаж, а данные временных рядов, такие как цены на товары, обменные курсы валют или другие рыночные цены, где история может дать полезную информацию о будущих тенденциях и степени неопределенности. | 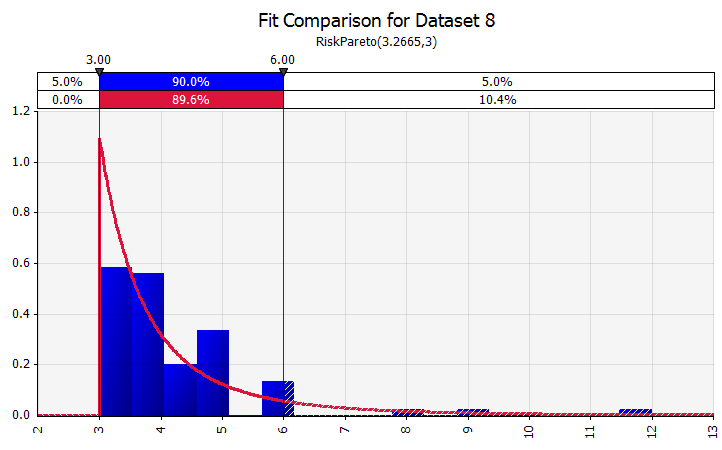 |
Объединение нескольких разных дистрибутивов в один. Чтобы смягчить потенциальное влияние индивидуальных предубеждений, часто бывает полезно включить в предположение информацию из различных источников и/или просмотреть и обсудить результаты. Существуют разные подходы:
| 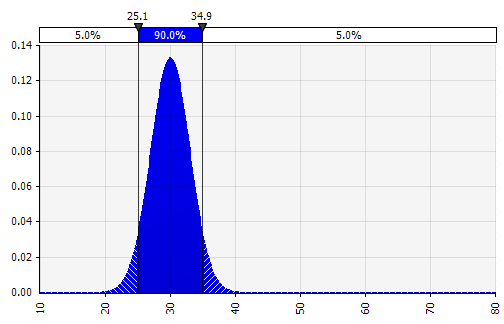 Вес: 20% 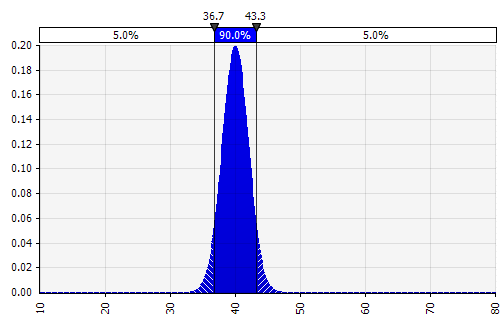 Вес: 20% 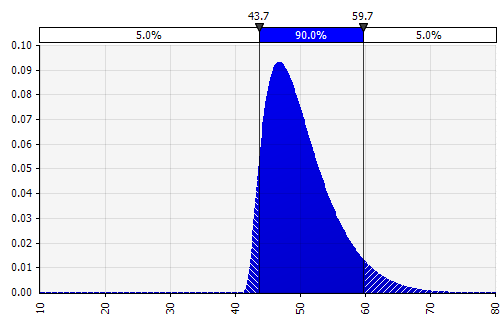 Вес: 60% 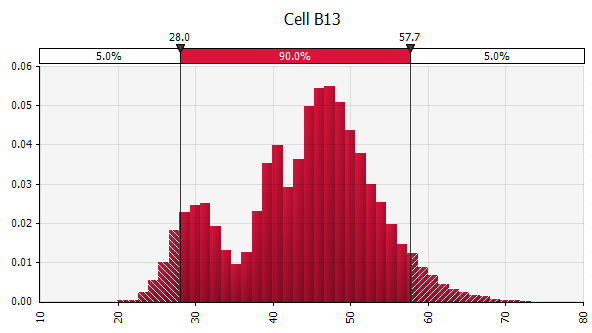 |
От руки. Чтобы быстро проиллюстрировать распределение в рамках обсуждений или если вам нужно распределение при составлении модели, которую нелегко создать из существующей палитры, полезна функциональность от руки. Как следует из названия, это позволяет рисовать распределение с помощью простого инструмента рисования. |  |
Теперь мы видим визуализацию распределения с несколькими параметрами в левой части. Символы среднего значения и стандартного отклонения должны выглядеть знакомыми. В случае нормального распределения средним значением будет то, что мы ранее ввели как одно значение в ячейку. Вот, например, распределение вероятностей продаж за 2018 год, где 10 % представляют собой среднее значение. В то время как ваша типичная модель фокусировалась бы только на цифре 10 % или имела бы «бычий» и «медвежий» сценарии с ростом, возможно, на 15 % и 5 % соответственно, теперь она предоставляет информацию о полном диапазоне ожидаемых потенциальных результатов.
Одним из преимуществ симуляций Монте-Карло является то, что маловероятные исходы хвоста могут вызвать размышления и дискуссии. Только отображение положительных и отрицательных сценариев может привести к риску того, что лица, принимающие решения, интерпретируют их как внешние границы, отвергая любые сценарии, лежащие за пределами. Это может привести к ошибочному принятию решений, с последствиями, которые лежат за пределами терпимости организации или отдельного лица к риску. Даже вероятность в 5% или 1% может оказаться неприемлемой, если рассматриваемый сценарий будет иметь катастрофические последствия.
Шаг 3. Расширение прогноза выручки с одного года до нескольких
При моделировании методом Монте-Карло помните о том, как распределения неопределенности и вероятности накладываются друг на друга, например, во времени. Давайте рассмотрим пример. Поскольку продажи в каждом году зависят от роста в предыдущие годы, мы можем визуализировать и увидеть, что наша оценка продаж в 2022 году более неопределенна, чем оценка для 2018 года (показана с использованием стандартных отклонений и 95% доверительных интервалов для каждого года). Для простоты в приведенном ниже примере указан рост за один год, 2018 г., а затем применяются те же темпы роста к каждому из следующих лет до 2022 г. Другой подход заключается в наличии пяти независимых распределений, по одному на каждый год.
Шаг 4. Продолжение вниз по отчету о прибылях и убытках — выражение маржи в виде вероятностных распределений
Теперь мы оцениваем распределение вероятностей для маржи EBIT в 2018 году (выделено ниже) аналогично тому, как мы делали это для роста продаж.
Здесь мы можем использовать функцию корреляции для моделирования ситуации, когда существует четкая корреляция между относительной долей рынка и прибыльностью, отражающая эффект масштаба. Сценарии с более высоким ростом продаж по сравнению с рынком и, соответственно, более высокой относительной долей рынка можно смоделировать так, чтобы они имели положительную корреляцию с более высокой маржой EBIT. В отраслях, где состояние фирмы сильно коррелирует с некоторыми другими внешними факторами, такими как цены на нефть или обменные курсы, определение распределения для этого фактора и моделирование корреляции с продажами и прибыльностью может иметь смысл.
В зависимости от доступного времени, размера транзакции и других факторов часто имеет смысл построить операционную модель и явно ввести наиболее неопределенные переменные. К ним относятся: объемы и цены продуктов, цены на товары, валютные курсы, ключевые статьи накладных расходов, ежемесячные активные пользователи и средний доход на единицу (ARPU). Также возможно моделировать переменные, выходящие за рамки количества, такие как время разработки, время выхода на рынок или скорость принятия рынком.
Шаг 5. Бухгалтерский баланс и отчет о движении денежных средств
Используя изложенный подход, мы теперь можем продолжить работу с балансовым отчетом и отчетом о движении денежных средств, внося допущения и используя распределения вероятностей там, где это имеет смысл.
Примечание по капитальным затратам: их можно смоделировать либо в абсолютных величинах, либо в процентах от продаж, возможно, в сочетании с более крупными пошаговыми инвестициями; производственное предприятие может, например, иметь четкий предел мощности и большие инвестиции в расширение или новое предприятие, необходимое, когда продажи превышают пороговое значение. Поскольку каждая из, скажем, 1000 или 10 000 итераций будет представлять собой полный пересчет модели, можно использовать простую формулу, которая запускает инвестиционные затраты, если/когда будет достигнут определенный объем.
Шаг 6. Доработка модели
Построение модели Монте-Карло имеет один дополнительный шаг по сравнению со стандартной финансовой моделью: ячейки, в которых мы хотим оценить результаты, должны быть специально обозначены как выходные ячейки. Программное обеспечение будет сохранять результаты каждой итерации моделирования для этих ячеек, чтобы мы могли оценить их после завершения моделирования. Все ячейки всей модели пересчитываются при каждой итерации, но результаты итераций в других ячейках, не обозначенных как входные или выходные, теряются и не могут быть проанализированы после завершения моделирования. Как вы можете видеть на снимке экрана ниже, мы назначаем ячейку результата MIRR выходной ячейкой.
После того, как вы закончили построение модели, пришло время запустить симуляцию в первый раз, просто нажав «начать симуляцию» и подождав несколько секунд.
Шаг 7. Интерпретация результатов
Выходы, выраженные как вероятности. В то время как наша модель ранее давала нам единственное значение модифицированной внутренней нормы доходности, теперь мы можем ясно видеть, что вокруг этого значения существует ряд потенциальных результатов с различной вероятностью. Это позволяет нам перефразировать такие вопросы, как «Сможем ли мы достичь нашей пороговой доходности с этими инвестициями?» на «Насколько вероятно, что мы достигнем или превзойдем нашу пороговую скорость?» Вы можете изучить, какие результаты наиболее вероятны, используя, например, доверительный интервал. Визуализация полезна при передаче результатов различным заинтересованным сторонам, и вы можете накладывать результаты других транзакций, чтобы визуально сравнить, насколько привлекательна и (не)надежна текущая транзакция по сравнению с другими (см. ниже).
Понимание степени неопределенности конечного результата. Если мы создадим диаграмму изменчивости денежного потока во времени, подобно тому, что мы сделали первоначально для продаж, станет ясно, что изменчивость свободного денежного потока становится значительной даже при относительно небольшой неопределенности в продажах и других входных данных, которые мы смоделировали как распределения вероятностей. , с результатами в диапазоне от 0,5 до 5,0 млн евро (коэффициент 10x) и даже всего одно стандартное отклонение от среднего. Это результат наложения неопределенных допущений друг на друга, эффект, который суммируется как «по вертикали» в течение многих лет, так и «по горизонтали» по финансовой отчетности. Визуализации предоставляют информацию об обоих типах неопределенности.
Анализ чувствительности: знакомство с графиком торнадо. Еще одна важная область — понять, какие входные данные оказывают наибольшее влияние на конечный результат. Классическим примером является то, как важности предположений о ставке дисконтирования или конечной стоимости часто придается слишком мало значения по сравнению с прогнозированием денежных потоков. Один из распространенных способов справиться с этим — использовать матрицы, в которых вы вводите одну клавишу на каждую ось, а затем вычисляете результат в каждой ячейке (см. ниже). Это особенно полезно в ситуациях, когда решения зависят от одного или нескольких ключевых предположений — в таких ситуациях «во что вы должны верить» лица, принимающие решения (например) в инвестиционном комитете, или группа высшего руководства могут иметь разные взгляды на эти ключевые предположения и матрица, подобная приведенной выше, позволяет каждому из них найти значение результата, соответствующее их мнению, и может принять решение, проголосовать или дать совет на основе этого.
Улучшение с помощью моделирования методом Монте-Карло. При использовании моделирования методом Монте-Карло этот подход можно дополнить другим: диаграммой торнадо. Эта визуализация перечисляет различные неопределенные входные данные и предположения по вертикальной оси, а затем показывает, насколько велико влияние каждого из них на конечный результат.
This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.
Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.
A Few Words of Caution: Different Types of Uncertainty
Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb
It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.
In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.
The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.
In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.
At the End of the Day, It's about the Mindset, Not the Technical Solution
There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.
I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.
Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.
I spend 98% of my time on 2% probabilities – Lloyd Blankfein
