Zestaw narzędzi prognostyka: Jak przeprowadzać symulacje Monte Carlo

Podsumowanie wykonawcze

Wstęp

Po pierwsze, jedyną pewnością jest to, że pewności nie ma. Po drugie, każda decyzja w konsekwencji jest kwestią ważenia prawdopodobieństw. Po trzecie, pomimo niepewności, musimy decydować i działać. I na koniec musimy oceniać decyzje nie tylko na podstawie wyników, ale także sposobu, w jaki te decyzje zostały podjęte. – Robert E. Rubin

Jednym z najważniejszych i najtrudniejszych aspektów prognozowania jest radzenie sobie z niepewnością związaną z badaniem przyszłości. Po zbudowaniu i zapełnieniu setek modeli finansowych i operacyjnych dla LBO, pozyskiwania funduszy dla startupów, budżetów, fuzji i przejęć oraz korporacyjnych planów strategicznych od 2003 roku, byłem świadkiem wielu różnych podejść do tego. Każdy dyrektor generalny, dyrektor finansowy, członek zarządu, inwestor lub członek komitetu inwestycyjnego wnosi własne doświadczenie i podejście do prognoz finansowych i niepewności — pod wpływem różnych zachęt. Często porównywanie rzeczywistych wyników z prognozami pozwala ocenić, jak duże mogą być odchylenia między prognozami a rzeczywistymi wynikami, a zatem potrzeba zrozumienia i wyraźnego uznania niepewności.

Początkowo używałem analiz scenariuszy i analiz wrażliwości do modelowania niepewności i nadal uważam je za bardzo przydatne narzędzia. Od czasu dodania symulacji Monte Carlo do mojego zestawu narzędzi w 2010 r. odkryłem, że są one niezwykle skutecznym narzędziem do udoskonalania i ulepszania sposobu myślenia o ryzyku i prawdopodobieństwach. Stosowałem to podejście do wszystkiego, od konstruowania wycen DCF, wyceny opcji kupna w przypadku fuzji i przejęć oraz omawiania ryzyka z kredytodawcami po poszukiwanie finansowania i kierowanie alokacją finansowania VC dla startupów. Podejście to zawsze było dobrze przyjmowane przez członków zarządu, inwestorów i zespoły kierownicze wyższego szczebla. W tym artykule przedstawiam krok po kroku samouczek dotyczący wykorzystania symulacji Monte Carlo w praktyce poprzez budowanie modelu wyceny DCF.

Każda decyzja jest kwestią ważenia prawdopodobieństw

Zanim zaczniemy od studium przypadku, przejrzyjmy kilka różnych podejść do radzenia sobie z niepewnością. Pojęcie wartości oczekiwanej — ważona prawdopodobieństwem średnia przepływów pieniężnych we wszystkich możliwych scenariuszach — to Finanse 101. Jednak specjaliści ds. finansów i szerzej decydenci stosują bardzo różne podejścia przy przekładaniu tego prostego spostrzeżenia na praktykę. Podejście to może obejmować z jednej strony po prostu nierozpoznawanie lub nie omawianie niepewności, z drugiej strony wyrafinowane modele i oprogramowanie. W niektórych przypadkach ludzie spędzają więcej czasu na omawianiu prawdopodobieństw niż na obliczaniu przepływów pieniężnych.

Oprócz tego, że po prostu nie zajmiemy się tym problemem, przeanalizujmy kilka sposobów radzenia sobie z niepewnością w prognozach średnio- i długoterminowych. Wiele z nich powinno być ci znajome.

Tworzenie jednego scenariusza. Takie podejście jest domyślne dla budżetów, wielu startupów, a nawet decyzji inwestycyjnych. Poza tym, że nie zawierają żadnych informacji na temat stopnia niepewności lub uznania, że ​​wyniki mogą różnić się od prognoz, mogą być niejednoznaczne i różnie interpretowane w zależności od interesariuszy. Niektórzy mogą zinterpretować to jako rozciągnięty cel, w którym rzeczywisty wynik jest bardziej prawdopodobny, aby był niższy niż przekroczony. Niektórzy postrzegają to jako bazową wydajność, która ma więcej plusów niż minusów. Inni mogą postrzegać to jako „przypadek podstawowy” z prawdopodobieństwem 50/50 w górę iw dół. W niektórych podejściach, zwłaszcza dla startupów, jest to bardzo ambitne i zdecydowanie bardziej prawdopodobnym rezultatem jest niepowodzenie lub niedobór, ale w celu uwzględnienia ryzyka stosuje się wyższą stopę dyskontową.	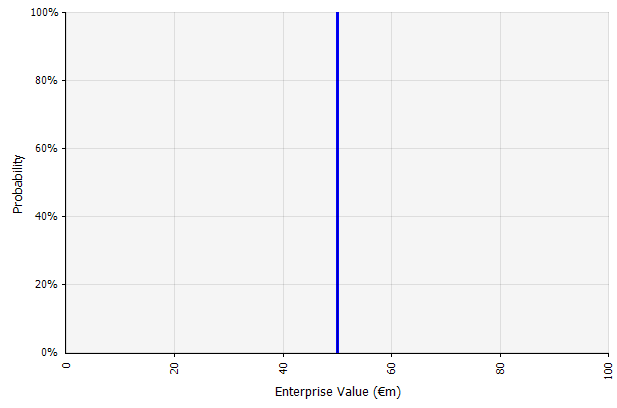Wszystkie dane wejściowe w długoterminowej prognozie przepływów pieniężnych w ramach tego podejścia są szacunkami punktowymi, co w tym przykładzie daje szacunkowy wynik punktowy w wysokości 50 mln EUR, z domniemanym prawdopodobieństwem 100%.
Tworzenie wielu scenariuszy. Takie podejście zakłada, że ​​rzeczywistość raczej nie rozwinie się zgodnie z jednym danym planem. 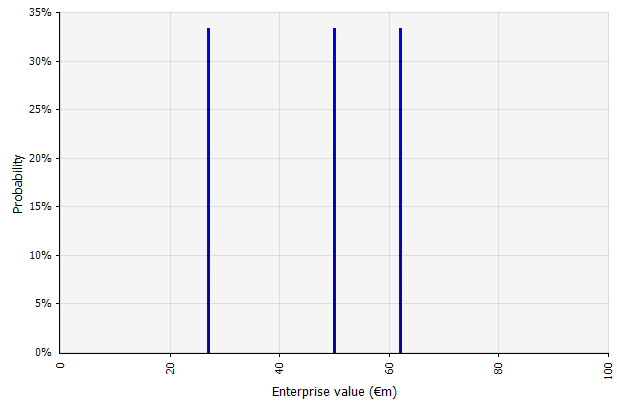W najprostszej formie, analiza wrażliwości, może to symulować wpływ np. wzrostu sprzedaży o 10% powyżej i poniżej scenariusza bazowego, wykorzystując daną kombinację kosztów stałych, półzmiennych i zmiennych do oszacowania wyniku finansowego. uderzenie. W bardziej złożonych formach myślisz o przyszłości z zupełnie innej perspektywy dla każdego scenariusza i analizujesz wpływ, jaki różne zmiany technologiczne, dynamika konkurencji i trendy makro będą miały na wyniki firmy. Często scenariusze są niestety wybierane dość arbitralnie, a czasem z myślą o pożądanym efekcie końcowym.	Trzy różne scenariusze dają trzy różne wyniki, tutaj założono, że są równie prawdopodobne. Nie są brane pod uwagę prawdopodobieństwa wyników poza scenariuszami wysokimi i niskimi.
Tworzenie przypadków bazowych, pozytywnych i negatywnych z wyraźnie rozpoznanym prawdopodobieństwem. Oznacza to, że przypadki niedźwiedzia i byka zawierają na przykład prawdopodobieństwo 25% w każdym ogonie, a oszacowanie wartości godziwej stanowi punkt środkowy. Użyteczną korzyścią z tego z perspektywy zarządzania ryzykiem jest wyraźna analiza ryzyka ogona, tj. zdarzeń poza scenariuszami zwyżkowymi i zniżkowymi.	Ilustracja z podręcznika wyceny Morningstar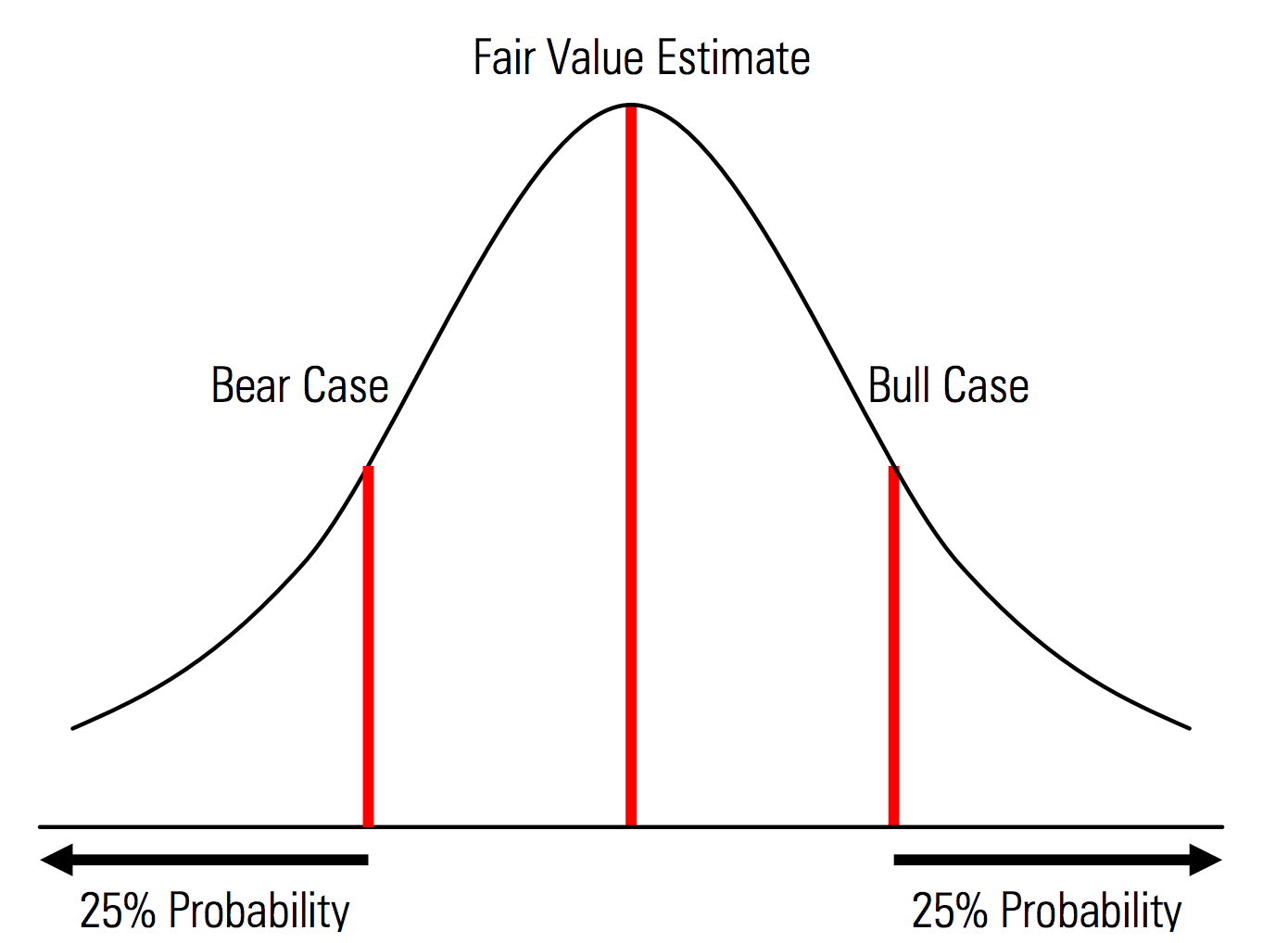
Wykorzystanie rozkładów prawdopodobieństwa i symulacji Monte Carlo. Korzystanie z rozkładów prawdopodobieństwa pozwala na modelowanie i wizualizację pełnego zakresu możliwych wyników w prognozie. Można to zrobić nie tylko na poziomie zagregowanym, ale także dla szczegółowych danych wejściowych, założeń i czynników. Metody Monte Carlo są następnie wykorzystywane do obliczania otrzymanych rozkładów prawdopodobieństwa na poziomie zagregowanym, co pozwala na analizę, w jaki sposób kilka niepewnych zmiennych wpływa na niepewność ogólnych wyników. Co być może najważniejsze, podejście zmusza wszystkich zaangażowanych w analizę i podejmowanie decyzji do wyraźnego rozpoznania niepewności związanej z prognozowaniem i myślenia według prawdopodobieństw. Podobnie jak inne podejścia, ma to swoje wady, w tym ryzyko fałszywej precyzji i wynikającej z niej nadmiernej pewności, która może się pojawić przy użyciu bardziej wyrafinowanego modelu, oraz dodatkowej pracy wymaganej do wybrania odpowiednich rozkładów prawdopodobieństwa i oszacowania ich parametrów, gdzie w przeciwnym razie tylko oszacowania punktowe byłyby używany.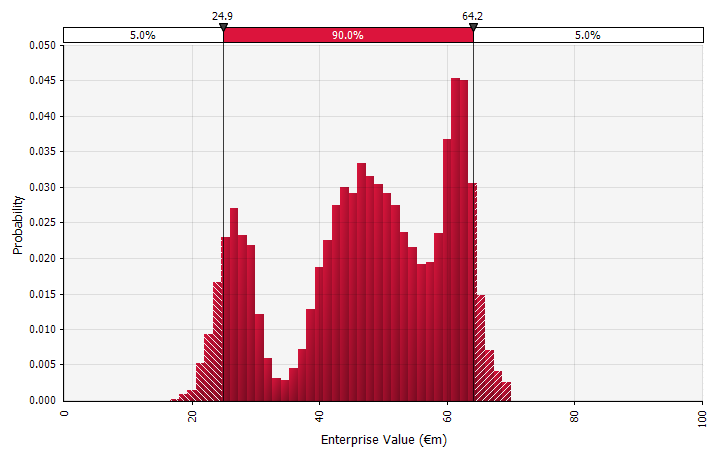

Co to jest symulacja Monte Carlo?

Symulacje Monte Carlo modelują prawdopodobieństwo różnych wyników w prognozach i szacunkach finansowych. Zasługują na swoją nazwę z obszaru Monte Carlo w Monako, który słynie na całym świecie z luksusowych kasyn; losowe wyniki są kluczowe dla tej techniki, podobnie jak w przypadku ruletki i automatów do gry. Symulacje Monte Carlo są przydatne w wielu dziedzinach, w tym w inżynierii, zarządzaniu projektami, wydobyciu ropy i gazu i innych kapitałochłonnych branżach, badaniach i rozwoju oraz ubezpieczeniach; tutaj skupiam się na zastosowaniach w finansach i biznesie.

Rozkłady prawdopodobieństwa

W symulacji niepewne dane wejściowe są opisane za pomocą rozkładów prawdopodobieństwa, opisanych parametrami, takimi jak średnia i odchylenie standardowe. Przykładowe dane wejściowe w prognozach finansowych mogą obejmować wszystko, od przychodów i marż po coś bardziej szczegółowego, takie jak ceny towarów, nakłady inwestycyjne na ekspansję lub kursy walutowe.

Gdy jeden lub więcej danych wejściowych jest opisanych jako rozkłady prawdopodobieństwa, dane wyjściowe również stają się rozkładami prawdopodobieństwa. Komputer losowo losuje liczbę z każdego rozkładu wejściowego i oblicza oraz zapisuje wynik. Jest to powtarzane setki, tysiące lub dziesiątki tysięcy razy, każdy nazywany iteracją. Łącznie te iteracje przybliżają rozkład prawdopodobieństwa końcowego wyniku.

Rodzaje wejść

Rozkłady wejściowe mogą być ciągłe , gdzie losowo generowana wartość może przyjąć dowolną wartość w rozkładzie (na przykład rozkład normalny) lub dyskretne , gdzie prawdopodobieństwa są przypisane do dwóch lub więcej różnych scenariuszy.

Symulacja może również zawierać kombinację rozkładów różnych typów. Weźmy na przykład farmaceutyczny projekt badawczo-rozwojowy z kilkoma etapami, z których każdy ma dyskretne prawdopodobieństwo sukcesu lub niepowodzenia. Można to połączyć z ciągłymi rozkładami opisującymi niepewne kwoty inwestycji potrzebne na każdym etapie i potencjalne przychody, jeśli projekt zaowocuje produktem, który trafi na rynek. Poniższy wykres przedstawia wyniki takiej symulacji: ~65% prawdopodobieństwa utraty całej inwestycji o wartości od 5 do 50 mln EUR (wartość bieżąca) oraz ~35% prawdopodobieństwa zysku netto najprawdopodobniej w przedziale 100 do 250 euro — informacje, które zostałyby utracone, gdyby kluczowe wskaźniki wyjściowe, takie jak MIRR lub NPV, były przedstawiane jako szacunki punktowe, a nie rozkłady prawdopodobieństwa.

Symulacje Monte Carlo w praktyce

Jednym z powodów, dla których symulacje Monte Carlo nie są szerzej stosowane, jest to, że typowe narzędzia codziennego użytku finansowego nie obsługują ich zbyt dobrze. Excel i Arkusze Google przechowują jeden wynik liczbowy lub formuły w każdej komórce i chociaż mogą definiować rozkłady prawdopodobieństwa i generować liczby losowe, budowanie od podstaw modelu finansowego z funkcjonalnością Monte Carlo jest kłopotliwe. I chociaż wiele instytucji finansowych i firm inwestycyjnych korzysta z symulacji Monte Carlo do wyceny instrumentów pochodnych, analizowania portfeli i nie tylko, ich narzędzia są zazwyczaj opracowywane we własnym zakresie, zastrzeżone lub zbyt drogie, co czyni je niedostępnymi dla indywidualnych specjalistów finansowych.

Dlatego chcę zwrócić uwagę na wtyczki Excela, takie jak @RISK firmy Palisade, ModelRisk firmy Vose i RiskAMP, które znacznie upraszczają pracę z symulacjami Monte Carlo i pozwalają zintegrować je z istniejącymi modelami. W poniższym przewodniku będę używał @RISK.

Studium przypadku: Prognozy przepływów pieniężnych z symulacją Monte Carlo

Przyjrzyjmy się prostemu przykładowi, który ilustruje kluczowe koncepcje symulacji Monte Carlo: pięcioletnia prognoza przepływów pieniężnych. W tym przewodniku konfiguruję i wypełniam podstawowy model przepływów pieniężnych do celów wyceny, stopniowo zastępuję dane wejściowe rozkładami prawdopodobieństwa, a na koniec przeprowadzam symulację i analizuję wyniki.

Krok 1. Wybór lub budowa modelu

Na początek korzystam z prostego modelu, skupionego na podkreśleniu kluczowych cech wykorzystania rozkładów prawdopodobieństwa. Zwróć uwagę, że na początek ten model nie różni się od żadnego innego modelu programu Excel; wtyczki, o których wspomniałem powyżej, działają z istniejącymi modelami i arkuszami kalkulacyjnymi. Poniższy model jest prostą, gotową wersją wypełnioną założeniami, aby stworzyć jeden scenariusz.

Krok 2. Tworzenie pierwszego rozkładu prawdopodobieństwa

Najpierw musimy zebrać informacje niezbędne do przyjęcia naszych założeń, a następnie wybrać właściwe rozkłady prawdopodobieństwa do wstawienia. Ważne jest, aby pamiętać, że źródło kluczowych danych wejściowych/założeń jest takie samo, niezależnie od tego, jakie podejście zastosujesz do radzenia sobie z niepewnością. Komercyjne due diligence, kompleksowy przegląd biznesplanu firmy w kontekście przewidywanego rozwoju rynku, trendów branżowych i dynamiki konkurencji, zazwyczaj obejmuje ekstrapolację danych historycznych, uwzględnienie opinii ekspertów, przeprowadzenie badań rynkowych i wywiady z uczestnikami rynku. Z mojego doświadczenia wynika, że ​​eksperci i uczestnicy rynku chętnie omawiają różne scenariusze, ryzyka i zakresy wyników. Jednak większość nie opisuje wprost rozkładów prawdopodobieństwa.

Przejdźmy teraz i zastąpmy nasze kluczowe wartości wejściowe rozkładami prawdopodobieństwa jeden po drugim, zaczynając od szacowanego wzrostu sprzedaży dla pierwszego roku prognozy (2018). Wtyczkę @RISK do programu Excel można przetestować w ramach 15-dniowej bezpłatnej wersji próbnej, dzięki czemu można ją pobrać ze strony internetowej Palisade i zainstalować za pomocą kilku kliknięć. Po włączeniu wtyczki @RISK wybierz komórkę, w której chcesz dystrybucję, i wybierz "Definiuj dystrybucję" w menu.

Następnie wybierasz jedną z pojawiającej się palety dystrybucji. Oprogramowanie @RISK oferuje ponad 70 różnych dystrybucji do wyboru, więc wybór jednej może początkowo wydawać się przytłaczający. Poniżej znajduje się przewodnik po garstce, z której najczęściej korzystam:

Normalna. Zdefiniowane przez średnią i odchylenie standardowe. Jest to dobry punkt wyjścia ze względu na swoją prostotę i nadaje się jako rozszerzenie podejścia Morningstar, w którym definiujesz rozkład, który obejmuje być może już zdefiniowane scenariusze lub zakresy dla danych danych wejściowych, zapewniając, że obserwacje są symetryczne wokół przypadku podstawowego i że prawdopodobieństwa w każdym ogonie wyglądają na rozsądne (powiedzmy 25%, jak w przykładzie Morningstar).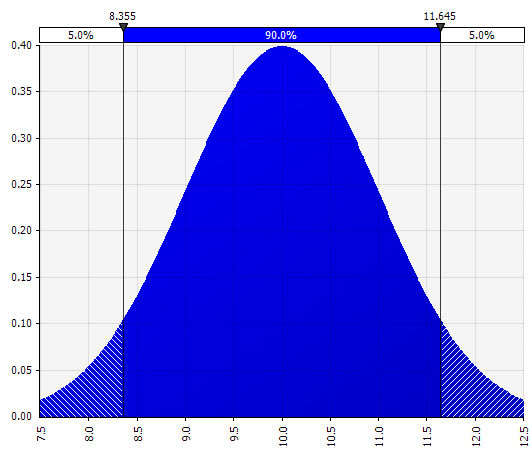
Chwile Johnsona. Wybranie tej opcji umożliwia zdefiniowanie rozkładów skośnych i rozkładów z grubszymi lub cieńszymi ogonami (technicznie dodając parametry skośności i kurtozy). Za kulisami wykorzystuje algorytm do wyboru jednego z czterech rozkładów, który odzwierciedla cztery wybrane parametry, ale jest to niewidoczne dla użytkownika --- wszystko, na czym musimy się skupić, to parametry. Czasami w trakcie zbierania informacji do danych wejściowych staje się jasne, że rozkład normalny nie jest odpowiedni. Na przykład w przypadku firmy znajdującej się w dołku lub szczycie cyklu branżowego prawdopodobieństwa lepszych lub gorszych wyników w ciągu następnych, powiedzmy, pięciu lat, nie będą symetryczne. Im bliżej szczytu, tym większe prawdopodobieństwo spadku w porównaniu z utrzymującymi się dobrymi wynikami. W tym przypadku przydatna może być dystrybucja skośna. Wiele napisano o pojęciu „grubych ogonów” w wielu dziedzinach finansów. Wydaje się, że rozkład normalny często nie opisuje zbyt dobrze rzeczywistych wyników, a zdarzenia, które powinny być bardzo rzadkie, występują częściej niż wskazywałby na to rozkład normalny.
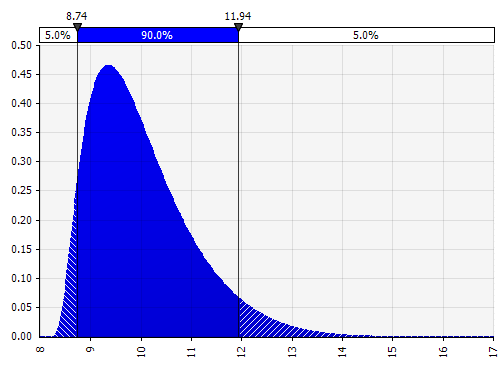Oddzielny. Gdzie prawdopodobieństwa są podane do dwóch lub więcej określonych wartości. Wracając do przykładu etapowego projektu badawczo-rozwojowego na początku, prawdopodobieństwo sukcesu na każdym etapie jest modelowane jako binarny rozkład dyskretny, z wynikiem 1 oznaczającym sukces i 0 niepowodzeniem.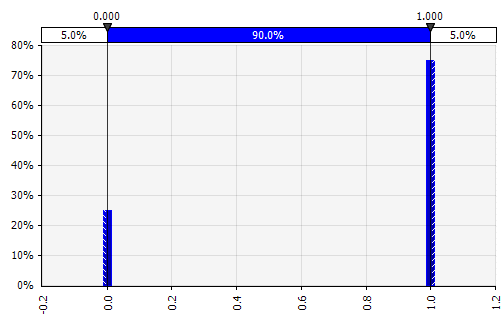
Dopasowanie dystrybucji. Gdy masz dużą liczbę historycznych punktów danych, przydatna jest funkcja dopasowywania rozkładu. Nie oznacza to, na przykład, trzech lub czterech lat historycznego wzrostu sprzedaży, ale dane szeregów czasowych, takie jak ceny towarów, kursy walut lub inne ceny rynkowe, w przypadku których historia może dostarczyć przydatnych informacji na temat przyszłych trendów i stopnia niepewności.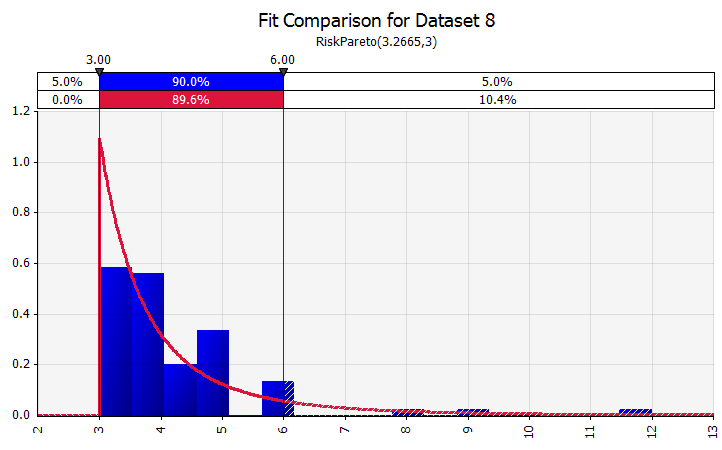
Łączenie kilku różnych dystrybucji w jedną. Aby złagodzić potencjalny wpływ indywidualnych uprzedzeń, często dobrym pomysłem jest uwzględnienie danych wejściowych z różnych źródeł w założeniu i/lub przegląd i omówienie wyników. Istnieją różne podejścia: 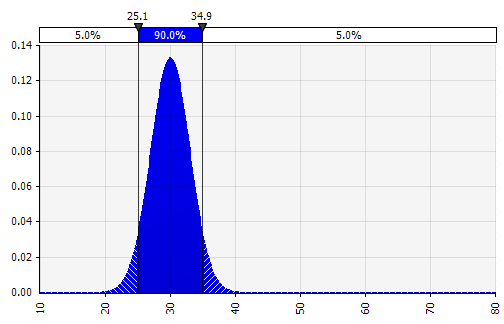Przygotuj szkic lub pierwszy pogląd, a następnie przejrzyj go z ekspertami, szerszym zespołem zarządzającym lub innymi decydentami. Wspólnie opracujcie najważniejsze dystrybucje podczas spotkania. Może to prowadzić do dobrej dyskusji i lepszych wyników, ale jak zwykle skład grupy ma kluczowe znaczenie; reprezentowanie różnych perspektyw/funkcji i wspieranie atmosfery energicznej, ale pełnej szacunku debaty są oczywiście pomocne. Opracuj jedną dystrybucję dla każdego kluczowego źródła i połącz je, ważone według tego, jak bardzo wierzysz w każde z nich. Jeśli otrzymujesz informacje od kilku różnych ekspertów, dobrym pomysłem może być umożliwienie każdemu z nich przedstawienia własnego poglądu, niezależnie od innych, a następnie połączenie w jeden. Funkcja @RISK MakeRiskInput robi to za nas.	Waga: 20% 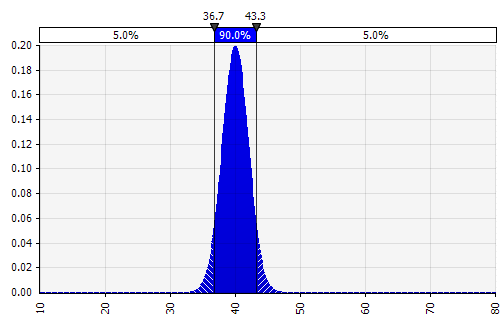+ Waga: 20% 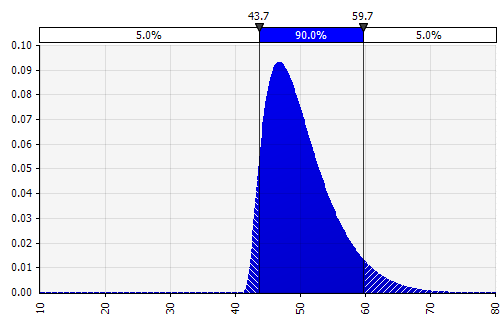+ Waga: 60% =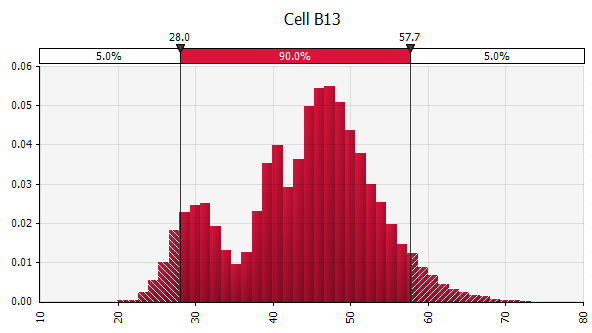
Odręczne. Aby szybko zilustrować rozkład jako część dyskusji lub jeśli potrzebujesz rozkładu podczas szkicowania modelu, który nie jest łatwy do utworzenia z istniejącej palety, przydatna jest funkcja odręczna. Jak sama nazwa wskazuje, pozwala to narysować rozkład za pomocą prostego narzędzia do malowania.

Teraz widzimy wizualizację rozkładu z kilkoma parametrami po lewej stronie. Symbole średniej i odchylenia standardowego powinny wyglądać znajomo. W przypadku rozkładu normalnego średnia byłaby tym, co wcześniej wprowadziliśmy jako pojedynczą wartość w komórce. Oto przykładowy rozkład prawdopodobieństwa sprzedaży z 2018 r., gdzie 10% reprezentuje średnią. Podczas gdy typowy model albo skupiałby się tylko na wartości 10%, albo miał scenariusze „byka” i „niedźwiedzia” z odpowiednio 15% i 5% wzrostem, teraz dostarcza on informacji o pełnym zakresie oczekiwanych potencjalnych wyników.

Jedną z zalet symulacji Monte Carlo jest to, że wyniki ogona o niskim prawdopodobieństwie mogą wywołać myślenie i dyskusje. Tylko pokazywanie scenariuszy w górę i w dół może wprowadzić ryzyko, że decydenci zinterpretują je jako granice zewnętrzne, odrzucając wszelkie scenariusze, które leżą poza. Może to skutkować błędnym podejmowaniem decyzji, z narażeniem na wyniki, które wykraczają poza tolerancję na ryzyko organizacji lub osoby. Nawet 5% lub 1% prawdopodobieństwa może być nie do zaakceptowania, jeśli dany scenariusz miałby katastrofalne konsekwencje.

Krok 3. Rozszerzenie prognozy przychodów z jednego roku na kilka

Korzystając z modelowania Monte Carlo, pamiętaj o tym, jak niepewność i rozkłady prawdopodobieństwa nakładają się na siebie, na przykład w czasie. Przyjrzyjmy się przykładowi. Ponieważ sprzedaż w każdym roku zależy od wzrostu w poprzednich, możemy zwizualizować i zobaczyć, że nasze szacunki dotyczące sprzedaży w 2022 r. są bardziej niepewne niż w 2018 r. (pokazane przy użyciu odchyleń standardowych i 95% przedziałów ufności w każdym roku). Dla uproszczenia poniższy przykład określa wzrost na rok 2018, a następnie stosuje tę samą stopę wzrostu do każdego z kolejnych lat do 2022. Innym podejściem jest posiadanie pięciu niezależnych rozkładów, po jednym na każdy rok.

Krok 4. Kontynuacja rachunku zysków i strat — wyrażanie marży jako rozkład prawdopodobieństwa

Szacujemy teraz rozkład prawdopodobieństwa dla marży EBIT w 2018 roku (podkreślony poniżej) podobnie jak zrobiliśmy to dla wzrostu sprzedaży.

Tutaj możemy użyć funkcji korelacji do symulacji sytuacji, w której istnieje wyraźna korelacja między względnym udziałem w rynku a rentownością, odzwierciedlając ekonomię skali. Scenariusze o wyższym wzroście sprzedaży w stosunku do rynku i odpowiednio wyższym względnym udziale w rynku można modelować tak, aby miały pozytywną korelację z wyższymi marżami EBIT. W branżach, w których fortuna firmy jest silnie skorelowana z innymi czynnikami zewnętrznymi, takimi jak ceny ropy naftowej lub kursy walut, określenie rozkładu dla tego czynnika i modelowanie korelacji ze sprzedażą i rentownością może mieć sens.

W zależności od dostępnego czasu, wielkości transakcji i innych czynników, często sensowne jest zbudowanie modelu operacyjnego i jawne wprowadzenie najbardziej niepewnych zmiennych. Obejmują one: wolumeny i ceny produktów, ceny towarów, kursy walutowe, kluczowe pozycje linii napowietrznych, miesięczną liczbę aktywnych użytkowników oraz średni przychód na jednostkę (ARPU). Możliwe jest również modelowanie poza zmiennymi ilościowymi, takimi jak czas opracowania, czas wprowadzenia na rynek lub wskaźnik przyjęcia na rynek.

Krok 5. Bilans i rachunek przepływów pieniężnych

Stosując nakreślone podejście, możemy teraz przejść do bilansu i rachunku przepływów pieniężnych, wypełniając założenia i stosując rozkłady prawdopodobieństwa tam, gdzie ma to sens.

Uwaga dotycząca nakładów inwestycyjnych: można je modelować w kwotach bezwzględnych lub jako procent sprzedaży, potencjalnie w połączeniu z większymi inwestycjami krokowymi; zakład produkcyjny może na przykład mieć wyraźny limit mocy i dużą inwestycję w rozbudowę lub nowy zakład niezbędny, gdy sprzedaż przekroczy próg. Ponieważ każda z powiedzmy 1000 lub 10 000 iteracji będzie całkowitym przeliczeniem modelu, można zastosować prostą formułę, która uruchamia koszt inwestycji, jeśli/kiedy zostanie osiągnięty określony wolumen.

Krok 6. Finalizacja modelu

Budowanie modelu Monte Carlo ma jeden dodatkowy krok w porównaniu ze standardowym modelem finansowym: komórki, w których chcemy ocenić wyniki, muszą być konkretnie oznaczone jako komórki wyjściowe. Oprogramowanie zapisze wyniki każdej iteracji symulacji dla tych komórek, abyśmy mogli je ocenić po zakończeniu symulacji. Wszystkie komórki w całym modelu są ponownie obliczane przy każdej iteracji, ale wyniki iteracji w innych komórkach, które nie są oznaczone jako komórki wejściowe lub wyjściowe, są tracone i nie mogą być analizowane po zakończeniu symulacji. Jak widać na poniższym zrzucie ekranu, oznaczamy komórkę wynikową MIRR jako komórkę wyjściową.

Po zakończeniu budowania modelu nadszedł czas, aby uruchomić symulację po raz pierwszy, po prostu naciskając „rozpocznij symulację” i odczekując kilka sekund.

Krok 7. Interpretacja wyników

Wyniki wyrażone jako prawdopodobieństwa. Podczas gdy nasz model wcześniej dawał nam pojedynczą wartość zmodyfikowanej wewnętrznej stopy zwrotu, teraz możemy wyraźnie zobaczyć, że istnieje wiele potencjalnych wyników wokół tej wartości, z różnymi prawdopodobieństwami. To pozwala nam przeformułować pytania, takie jak „Czy dzięki tej inwestycji osiągniemy naszą przeszkodę w postaci stopy zwrotu?” na „Jak prawdopodobne jest, że osiągniemy lub przekroczymy nasz wskaźnik przeszkód?” Możesz zbadać, które wyniki są najbardziej prawdopodobne, korzystając na przykład z przedziału ufności. Wizualizacja jest pomocna podczas komunikowania wyników różnym interesariuszom, a wyniki innych transakcji można nakładać na siebie, aby wizualnie porównać, jak atrakcyjna i (nie)pewna jest bieżąca transakcja w porównaniu z innymi (patrz poniżej).

Zrozumienie stopnia niepewności w wyniku końcowym. Jeśli wygenerujemy wykres zmienności przepływów pieniężnych w czasie, podobny do tego, który zrobiliśmy początkowo dla sprzedaży, staje się jasne, że zmienność wolnych przepływów pieniężnych staje się istotna nawet przy stosunkowo niewielkiej niepewności sprzedaży i innych danych wejściowych, które modelowaliśmy jako rozkłady prawdopodobieństwa , z wynikami wahającymi się od około 0,5 mln EUR do 5,0 mln EUR — współczynnik 10-krotny — nawet jedno odchylenie standardowe od średniej. Jest to wynik nakładania na siebie niepewnych założeń, efekt, który składa się zarówno „pionowo” na przestrzeni lat, jak i „poziomo” w dół sprawozdania finansowego. Wizualizacje dostarczają informacji o obu rodzajach niepewności.

Analiza wrażliwości: Przedstawiamy wykres tornada. Innym ważnym obszarem jest zrozumienie, które dane wejściowe mają największy wpływ na końcowy wynik. Klasycznym przykładem jest to, że ważności założeń dotyczących stopy dyskontowej lub wartości końcowej często przypisuje się zbyt małą wagę w stosunku do prognozowania przepływów pieniężnych. Jednym z typowych sposobów radzenia sobie z tym jest użycie macierzy, w których umieszczasz jedno kluczowe dane wejściowe na każdej osi, a następnie obliczasz wynik w każdej komórce (patrz poniżej). Jest to przydatne zwłaszcza w sytuacjach, w których decyzje zależą od jednego lub kilku kluczowych założeń — w sytuacjach „w co trzeba wierzyć” decydenci (na przykład) z komitetu inwestycyjnego lub wyższego kierownictwa mogą mieć różne poglądy na temat te kluczowe założenia, a macierz, taka jak powyższa, pozwala każdemu z nich znaleźć wartość wynikową odpowiadającą ich opinii i na tej podstawie może decydować, głosować lub udzielać porad.

Wzmacnianie za pomocą symulacji Monte Carlo. Korzystając z symulacji Monte Carlo, podejście to można uzupełnić innym: diagramem tornada. Ta wizualizacja przedstawia różne niepewne dane wejściowe i założenia na osi pionowej, a następnie pokazuje, jak duży wpływ każdego z nich ma na wynik końcowy.

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein