กล่องเครื่องมือของผู้พยากรณ์: วิธีดำเนินการจำลองมอนติคาร์โล

บทสรุปผู้บริหาร

บทนำ

ประการแรก ความแน่นอนเพียงอย่างเดียวคือไม่มีความแน่นอน ประการที่สอง การตัดสินใจทุกครั้งเป็นเรื่องของความน่าจะเป็นในการชั่งน้ำหนัก สาม เราต้องตัดสินใจและต้องลงมือทำทั้งๆ ที่ความไม่แน่นอน และสุดท้าย เราต้องตัดสินการตัดสินใจ ไม่เพียงแต่ผลลัพธ์เท่านั้น แต่ยังต้องตัดสินด้วยว่าตัดสินใจอย่างไร – โรเบิร์ต อี. รูบิน

แง่มุมที่สำคัญและท้าทายที่สุดประการหนึ่งของการคาดการณ์คือการจัดการกับความไม่แน่นอนที่มีอยู่ในการตรวจสอบอนาคต หลังจากสร้างและจัดทำแบบจำลองทางการเงินและการดำเนินงานหลายร้อยรูปแบบสำหรับ LBO การระดมทุนสำหรับสตาร์ทอัพ งบประมาณ การควบรวมกิจการ และแผนกลยุทธ์ขององค์กรมาตั้งแต่ปี 2546 ฉันได้เห็นวิธีการที่หลากหลายในการทำเช่นนั้น CEO, CFO, สมาชิกคณะกรรมการ, นักลงทุน หรือคณะกรรมการการลงทุนทุกคนต่างนำประสบการณ์และแนวทางของตนเองมาใช้กับการคาดการณ์ทางการเงินและความไม่แน่นอน ซึ่งได้รับอิทธิพลจากสิ่งจูงใจที่แตกต่างกัน บ่อยครั้ง การเปรียบเทียบผลลัพธ์ที่เกิดขึ้นจริงกับการคาดการณ์จะทำให้เห็นค่าความเบี่ยงเบนระหว่างการคาดการณ์และผลลัพธ์ที่เกิดขึ้นจริงได้มากเพียงใด ดังนั้นจึงจำเป็นต้องทำความเข้าใจและตระหนักถึงความไม่แน่นอนอย่างชัดเจน

ตอนแรกฉันเริ่มใช้การวิเคราะห์สถานการณ์และความไวต่อความไม่แน่นอนของแบบจำลอง และยังคงพิจารณาว่าสิ่งเหล่านี้เป็นเครื่องมือที่มีประโยชน์มาก ตั้งแต่เพิ่มการจำลอง Monte Carlo ลงในกล่องเครื่องมือของฉันในปี 2010 ฉันพบว่าสิ่งเหล่านี้เป็นเครื่องมือที่มีประสิทธิภาพอย่างยิ่งในการปรับแต่งและปรับปรุงวิธีคิดของคุณเกี่ยวกับความเสี่ยงและความน่าจะเป็น ฉันได้ใช้แนวทางสำหรับทุกอย่างตั้งแต่การสร้างการประเมินมูลค่า DCF การประเมินมูลค่าตัวเลือกการโทรในการควบรวมกิจการ และหารือเกี่ยวกับความเสี่ยงกับผู้ให้กู้ไปจนถึงการหาเงินทุนและแนวทางการจัดสรรเงินทุน VC สำหรับสตาร์ทอัพ แนวทางนี้ได้รับการตอบรับอย่างดีจากสมาชิกคณะกรรมการ นักลงทุน และทีมผู้บริหารระดับสูง ในบทความนี้ ฉันมีบทแนะนำทีละขั้นตอนเกี่ยวกับการใช้การจำลองแบบมอนติคาร์โลในทางปฏิบัติโดยการสร้างแบบจำลองการประเมินค่า DCF

ทุกการตัดสินใจเป็นเรื่องของความน่าจะเป็นในการชั่งน้ำหนัก

ก่อนเริ่มกรณีศึกษา เรามาทบทวนแนวทางต่างๆ สองสามวิธีในการจัดการกับความไม่แน่นอนกันก่อน แนวคิดของมูลค่าที่ คาดหวัง — ค่า เฉลี่ยถ่วงน้ำหนักของความน่าจะเป็นของกระแสเงินสดในทุกสถานการณ์ที่เป็นไปได้—คือ Finance 101 แต่ผู้เชี่ยวชาญด้านการเงินและผู้มีอำนาจตัดสินใจในวงกว้างกว่านั้น ใช้แนวทางที่แตกต่างกันมากเมื่อแปลข้อมูลเชิงลึกที่เรียบง่ายนี้เป็นการปฏิบัติ แนวทางดังกล่าวอาจมีตั้งแต่การไม่รับรู้หรือพูดคุยถึงความไม่แน่นอนเลย ไปจนถึงรูปแบบที่ซับซ้อนและซอฟต์แวร์ในอีกทางหนึ่ง ในบางกรณี ผู้คนมักใช้เวลาพูดคุยเกี่ยวกับความน่าจะเป็นมากกว่าการคำนวณกระแสเงินสด

นอกจากจะไม่พูดถึงมันแล้ว เรามาพิจารณาสองสามวิธีในการจัดการกับความไม่แน่นอนในการประมาณการระยะกลางหรือระยะยาว หลายสิ่งเหล่านี้น่าจะคุ้นเคยกับคุณ

การสร้างสถานการณ์หนึ่ง แนวทางนี้เป็นค่าเริ่มต้นสำหรับงบประมาณ สตาร์ทอัพจำนวนมาก และแม้แต่การตัดสินใจลงทุน นอกจากจะไม่มีข้อมูลใดๆ เกี่ยวกับระดับของความไม่แน่นอนหรือการรับรู้ว่าผลลัพธ์อาจแตกต่างจากที่คาดการณ์ไว้ ยังสามารถคลุมเครือและตีความได้แตกต่างกันตามผู้มีส่วนได้ส่วนเสีย บางคนอาจตีความว่าเป็นเป้าหมายที่ยืดเยื้อ ซึ่งผลลัพธ์ที่แท้จริงมักจะสั้นกว่าเกิน บางคนมองว่าเป็นประสิทธิภาพพื้นฐานที่มีข้อดีมากกว่าข้อเสีย คนอื่นอาจมองว่าเป็น "กรณีพื้นฐาน" ที่มีโอกาสขึ้นและลง 50/50 ในบางแนวทาง โดยเฉพาะอย่างยิ่งสำหรับสตาร์ทอัพ มีความทะเยอทะยานอย่างมาก และความล้มเหลวหรือการขาดแคลนเป็นผลลัพธ์ที่น่าจะเป็นไปได้มากกว่า แต่อัตราการคิดลดที่สูงกว่านั้นถูกใช้เพื่อพยายามพิจารณาความเสี่ยง	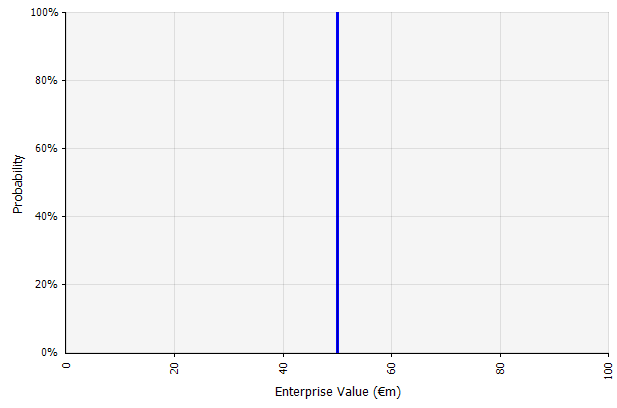ข้อมูลที่ป้อนเข้าในการคาดการณ์กระแสเงินสดในระยะยาวภายใต้แนวทางนี้คือการประมาณการแบบจุดทั้งหมด โดยให้ผลการประมาณแบบจุดที่ 50 ล้านยูโรในตัวอย่างนี้ โดยมีความน่าจะเป็นโดยปริยายที่ 100%
การสร้างหลายสถานการณ์ แนวทางนี้ตระหนักดีว่าความเป็นจริงไม่น่าจะเกิดขึ้นตามแผนที่กำหนดไว้เพียงแผนเดียว 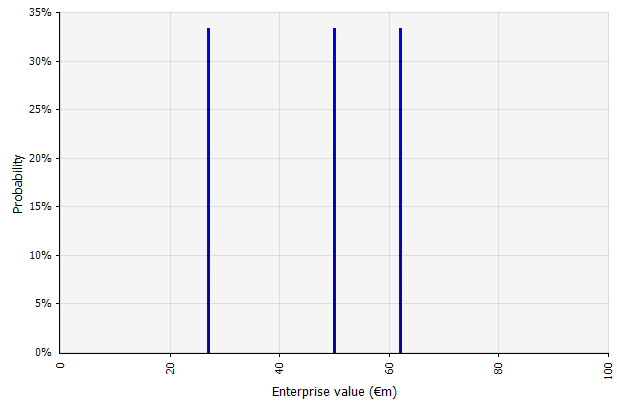ในรูปแบบที่ง่ายที่สุด การวิเคราะห์ความอ่อนไหว สิ่งนี้สามารถจำลองผลกระทบของยอดขาย เช่น การเติบโตของยอดขาย 10% ที่สูงกว่าและต่ำกว่ากรณีพื้นฐาน โดยใช้ต้นทุนคงที่ กึ่งตัวแปร และต้นทุนผันแปรที่กำหนดเพื่อประมาณการบรรทัดล่าง ผลกระทบ. ในรูปแบบที่ซับซ้อนมากขึ้น คุณคิดถึงอนาคตจากมุมมองที่แตกต่างกันโดยสิ้นเชิงสำหรับแต่ละสถานการณ์ และวิเคราะห์ผลกระทบที่การพัฒนาทางเทคโนโลยีที่แตกต่างกัน พลวัตของการแข่งขัน และแนวโน้มมหภาคจะมีต่อประสิทธิภาพของบริษัท บ่อยครั้ง สถานการณ์ต่างๆ มักถูกเลือกโดยพลการ และบางครั้งก็มีผลลัพธ์ที่ต้องการในใจ	สถานการณ์ที่แตกต่างกันสามแบบให้ผลลัพธ์ที่แตกต่างกันสามแบบ ซึ่งถือว่ามีโอกาสเท่าเทียมกัน ไม่พิจารณาความน่าจะเป็นของผลลัพธ์นอกสถานการณ์สูงและต่ำ
การสร้างกรณีฐาน กลับด้าน และด้านลบที่มีความน่าจะเป็นที่รับรู้อย่างชัดเจน กล่าวคือ กรณีหมีและตลาดกระทิงมีความน่าจะเป็น 25% ในแต่ละหาง และการประมาณมูลค่ายุติธรรมแสดงถึงจุดกึ่งกลาง ประโยชน์ที่เป็นประโยชน์ของสิ่งนี้จากมุมมองของการจัดการความเสี่ยงคือการวิเคราะห์ความเสี่ยงหางอย่างชัดเจน เช่น เหตุการณ์ที่อยู่นอกสถานการณ์กลับหัวและขาลง	ภาพประกอบจากคู่มือการประเมินมูลค่า Morningstar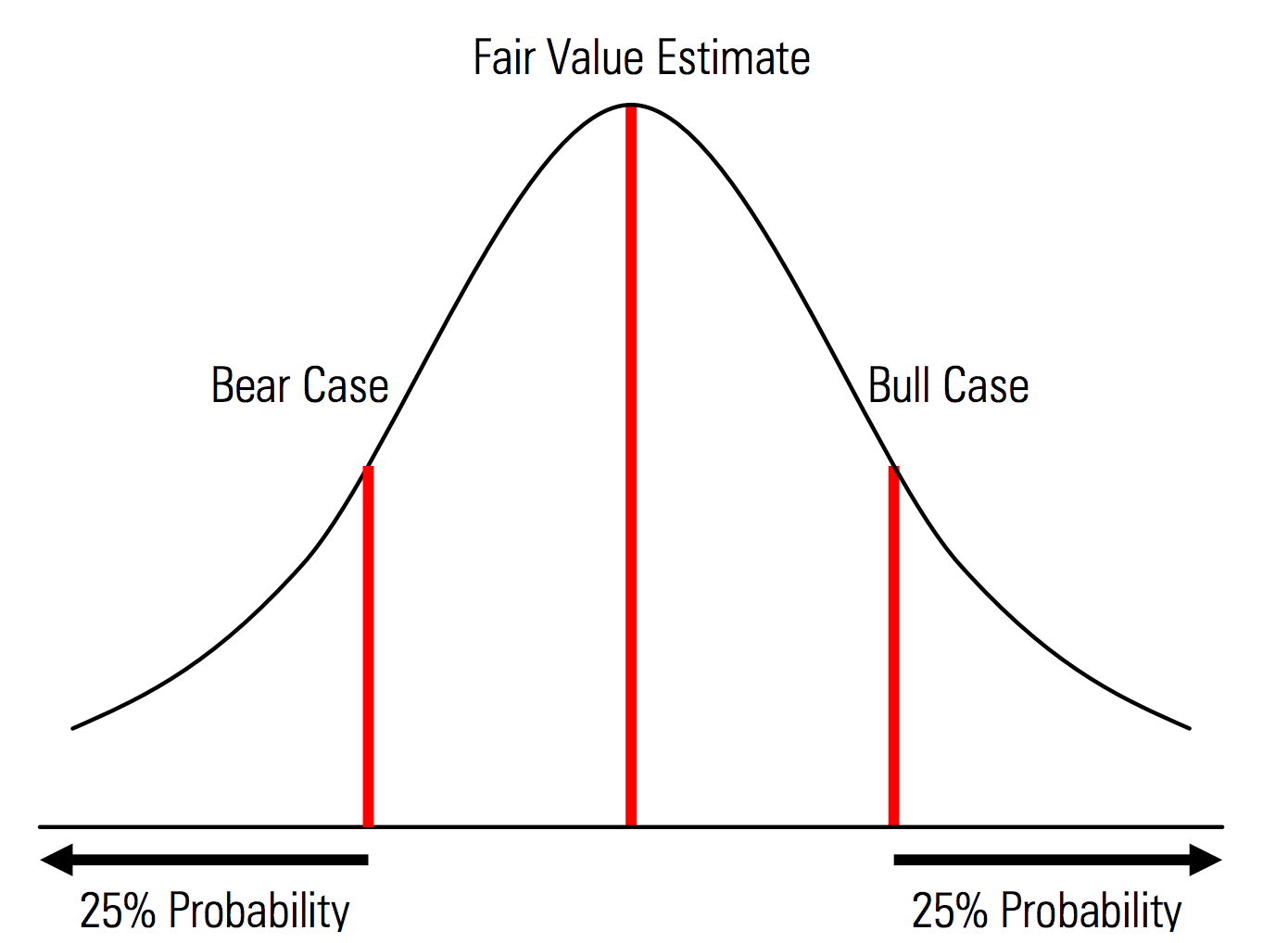
การใช้การแจกแจงความน่าจะเป็นและการจำลองแบบมอนติคาร์โล การใช้การแจกแจงความน่าจะเป็นช่วยให้คุณสร้างแบบจำลองและเห็นภาพผลลัพธ์ที่เป็นไปได้ทั้งหมดในการคาดการณ์ สิ่งนี้สามารถทำได้ไม่เพียงแต่ในระดับรวมเท่านั้น แต่ยังสำหรับข้อมูลอินพุต สมมติฐาน และตัวขับเคลื่อนโดยละเอียดแต่ละรายการ จากนั้นใช้วิธีมอนติคาร์โลในการคำนวณการแจกแจงความน่าจะเป็นที่เป็นผลลัพธ์ในระดับรวม เพื่อให้สามารถวิเคราะห์ว่าตัวแปรที่ไม่แน่นอนหลายตัวมีส่วนทำให้เกิดความไม่แน่นอนของผลลัพธ์โดยรวมได้อย่างไร บางทีสิ่งสำคัญที่สุดคือแนวทางนี้บังคับให้ทุกคนที่เกี่ยวข้องในการวิเคราะห์และตัดสินใจรับรู้อย่างชัดเจนถึงความไม่แน่นอนที่มีอยู่ในการคาดการณ์และคิดในความน่าจะเป็น เช่นเดียวกับวิธีอื่นๆ วิธีนี้ก็มีข้อเสีย รวมถึงความเสี่ยงจากความแม่นยำที่ผิดพลาดและส่งผลให้เกิดความมั่นใจมากเกินไปซึ่งอาจมาพร้อมกับการใช้แบบจำลองที่ซับซ้อนยิ่งขึ้น และงานเพิ่มเติมที่จำเป็นในการเลือกการแจกแจงความน่าจะเป็นที่เหมาะสมและประมาณค่าพารามิเตอร์ของพวกมัน ใช้แล้ว.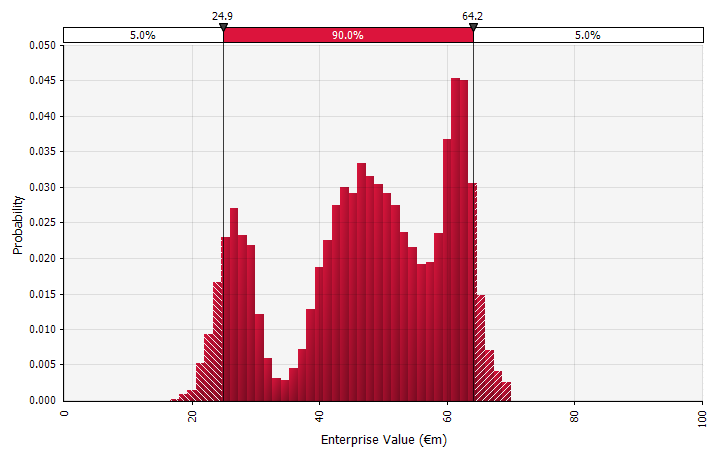

การจำลอง Monte Carlo คืออะไร?

การจำลองแบบมอนติคาร์โลจำลองความน่าจะเป็นของผลลัพธ์ที่แตกต่างกันในการคาดการณ์และการประมาณการทางการเงิน พวกเขาได้รับชื่อจากพื้นที่ Monte Carlo ในโมนาโกซึ่งมีชื่อเสียงระดับโลกในด้านคาสิโนระดับไฮเอนด์ ผลลัพธ์แบบสุ่มเป็นศูนย์กลางของเทคนิค เช่นเดียวกับรูเล็ตและสล็อตแมชชีน การจำลองมอนติคาร์โลมีประโยชน์ในหลากหลายสาขา รวมถึงวิศวกรรม การจัดการโครงการ การสำรวจน้ำมันและก๊าซ และอุตสาหกรรมอื่นๆ ที่ใช้เงินทุนสูง การวิจัยและพัฒนา และการประกันภัย ที่นี่ฉันเน้นการใช้งานในด้านการเงินและธุรกิจ

การแจกแจงความน่าจะเป็น

ในการจำลอง อินพุตที่ไม่แน่นอนจะอธิบายโดยใช้การแจกแจงความน่าจะเป็น ซึ่งอธิบายโดยพารามิเตอร์ เช่น ค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน ตัวอย่างข้อมูลที่ป้อนเข้าในประมาณการทางการเงินอาจเป็นอะไรก็ได้ตั้งแต่รายได้และส่วนต่างไปจนถึงรายละเอียดที่ละเอียดยิ่งขึ้น เช่น ราคาสินค้าโภคภัณฑ์ ค่าใช้จ่ายลงทุนเพื่อการขยาย หรืออัตราแลกเปลี่ยนเงินตราต่างประเทศ

เมื่อมีการอธิบายอินพุตอย่างน้อยหนึ่งรายการเป็นการแจกแจงความน่าจะเป็น ผลลัพธ์จะกลายเป็นการแจกแจงความน่าจะเป็นด้วย คอมพิวเตอร์จะสุ่มตัวเลขจากการแจกแจงอินพุตแต่ละครั้ง และคำนวณและบันทึกผลลัพธ์ สิ่งนี้ซ้ำแล้วซ้ำอีกหลายร้อย หลายพัน หรือหลายหมื่นครั้ง ซึ่งแต่ละครั้งเรียกว่าการวนซ้ำ เมื่อนำมารวมกัน การวนซ้ำเหล่านี้จะประมาณการกระจายความน่าจะเป็นของผลลัพธ์สุดท้าย

ประเภทของอินพุต

การแจกแจงอินพุตอาจเป็นแบบ ต่อเนื่อง โดยที่ค่าที่สร้างแบบสุ่มสามารถรับค่าใดก็ได้ภายใต้การแจกแจง (เช่น การแจกแจงแบบปกติ) หรือ แบบไม่ต่อเนื่อง โดยที่ความน่าจะเป็นจะแนบอยู่กับสถานการณ์ที่แตกต่างกันสองสถานการณ์ขึ้นไป

การจำลองยังสามารถประกอบด้วยการแจกแจงประเภทต่างๆ ยกตัวอย่างเช่น โครงการ R&D ด้านเภสัชกรรมที่มีหลายขั้นตอนซึ่งแต่ละขั้นตอนมีโอกาสสำเร็จหรือล้มเหลวแยกกัน สามารถใช้ร่วมกับการแจกแจงแบบต่อเนื่องที่อธิบายจำนวนเงินลงทุนที่ไม่แน่นอนซึ่งจำเป็นสำหรับแต่ละขั้นตอนและรายได้ที่เป็นไปได้หากโครงการส่งผลให้ผลิตภัณฑ์ที่เข้าถึงตลาด แผนภูมิด้านล่างแสดงผลลัพธ์จากการจำลองดังกล่าว: ความน่าจะเป็น ~65% ที่จะสูญเสียการลงทุนทั้งหมด 5 ล้านยูโรถึง 50 ล้านยูโร (มูลค่าปัจจุบัน) และความน่าจะเป็น ~35% ของกำไรสุทธิที่มีแนวโน้มมากที่สุดในช่วง €100 ถึง €250—ข้อมูลที่จะหายไปหากตัวชี้วัดผลลัพธ์ที่สำคัญ เช่น MIRR หรือ NPV ถูกแสดงเป็นการประมาณการแบบจุดมากกว่าการแจกแจงความน่าจะเป็น

การจำลอง Monte Carlo ในทางปฏิบัติ

เหตุผลหนึ่งที่การจำลองแบบ Monte Carlo ไม่ได้ใช้กันอย่างแพร่หลายเพราะเครื่องมือทางการเงินในแต่ละวันโดยทั่วไปไม่สนับสนุนเครื่องมือเหล่านี้เป็นอย่างดี Excel และ Google ชีตมีตัวเลขหรือผลลัพธ์หนึ่งสูตรในแต่ละเซลล์ และถึงแม้จะสามารถกำหนดการกระจายความน่าจะเป็นและสร้างตัวเลขสุ่มได้ การสร้างแบบจำลองทางการเงินด้วยฟังก์ชันมอนติคาร์โลตั้งแต่เริ่มต้นนั้นค่อนข้างยุ่งยาก และในขณะที่สถาบันการเงินและบริษัทการลงทุนหลายแห่งใช้การจำลองแบบมอนติคาร์โลเพื่อประเมินมูลค่าตราสารอนุพันธ์ วิเคราะห์พอร์ตโฟลิโอ และอื่นๆ เครื่องมือของพวกเขามักได้รับการพัฒนาขึ้นเองภายในบริษัท มีกรรมสิทธิ์หรือมีราคาแพงมาก ทำให้ไม่สามารถเข้าถึงผู้เชี่ยวชาญด้านการเงินแต่ละรายได้

ดังนั้นฉันจึงต้องการดึงความสนใจไปที่ปลั๊กอินของ Excel เช่น @RISK โดย Palisade, ModelRisk โดย Vose และ RiskAMP ซึ่งทำให้การทำงานกับการจำลองแบบ Monte Carlo ง่ายขึ้นอย่างมาก และช่วยให้คุณสามารถรวมเข้ากับแบบจำลองที่มีอยู่ได้ ในคำแนะนำต่อไปนี้ ฉันจะใช้ @RISK

กรณีศึกษา: การคาดการณ์กระแสเงินสดด้วยการจำลองมอนติคาร์โล

ให้เราทบทวนตัวอย่างง่ายๆ ที่แสดงให้เห็นแนวคิดหลักของการจำลองมอนติคาร์โล: การคาดการณ์กระแสเงินสดห้าปี ในคำแนะนำนี้ ฉันตั้งค่าและเติมโมเดลกระแสเงินสดพื้นฐานสำหรับวัตถุประสงค์ในการประเมินมูลค่า ค่อยๆ แทนที่อินพุตด้วยการแจกแจงความน่าจะเป็น และสุดท้ายเรียกใช้การจำลองและวิเคราะห์ผลลัพธ์

ขั้นตอนที่ 1 การเลือกหรือสร้างแบบจำลอง

ในการเริ่มต้น ฉันใช้แบบจำลองอย่างง่าย โดยเน้นที่การเน้นคุณลักษณะหลักของการใช้การแจกแจงความน่าจะเป็น โปรดทราบว่าในการเริ่มต้น โมเดลนี้ไม่แตกต่างจากโมเดล Excel อื่นๆ ปลั๊กอินที่ฉันกล่าวถึงข้างต้นใช้งานได้กับโมเดลและสเปรดชีตที่มีอยู่ของคุณ โมเดลด้านล่างเป็นเวอร์ชันที่ไม่มีวางจำหน่ายทั่วไปโดยมีการสันนิษฐานเพื่อสร้างสถานการณ์เดียว

ขั้นตอนที่ 2 การสร้างการกระจายความน่าจะเป็นครั้งแรก

อันดับแรก เราต้องรวบรวมข้อมูลที่จำเป็นสำหรับการตั้งสมมติฐาน จากนั้นเราต้องเลือกการแจกแจงความน่าจะเป็นที่ถูกต้องเพื่อแทรก สิ่งสำคัญคือต้องทราบว่าแหล่งที่มาของข้อมูลเข้า/ข้อสันนิษฐานที่สำคัญเหมือนกัน ไม่ว่าคุณจะใช้แนวทางใดในการจัดการกับความไม่แน่นอน การตรวจสอบวิเคราะห์สถานะเชิงพาณิชย์ การทบทวนแผนธุรกิจของบริษัทอย่างครอบคลุมในบริบทของการพัฒนาตลาดที่คาดการณ์ไว้ แนวโน้มของอุตสาหกรรม และการเปลี่ยนแปลงของการแข่งขัน โดยทั่วไปจะรวมถึงการอนุมานจากข้อมูลในอดีต ผสมผสานความคิดเห็นของผู้เชี่ยวชาญ การวิจัยตลาด และการสัมภาษณ์ผู้เข้าร่วมตลาด จากประสบการณ์ของผม ผู้เชี่ยวชาญและผู้เข้าร่วมตลาดยินดีที่จะหารือเกี่ยวกับสถานการณ์ ความเสี่ยง และช่วงของผลลัพธ์ที่แตกต่างกัน อย่างไรก็ตาม ส่วนใหญ่ไม่ได้อธิบายการแจกแจงความน่าจะเป็นอย่างชัดเจน

ให้เราอธิบายและแทนที่ค่าอินพุตหลักของเราด้วยการแจกแจงความน่าจะเป็นทีละรายการ โดยเริ่มจากการเติบโตของยอดขายโดยประมาณสำหรับปีที่คาดการณ์ครั้งแรก (2018) ปลั๊กอิน @RISK สำหรับ Excel สามารถประเมินได้ด้วยการทดลองใช้ฟรี 15 วัน คุณจึงสามารถดาวน์โหลดได้จากเว็บไซต์ Palisade และติดตั้งด้วยการคลิกเพียงไม่กี่ครั้ง เมื่อเปิดใช้งานปลั๊กอิน @RISK ให้เลือกเซลล์ที่คุณต้องการให้มีการแจกจ่ายและเลือก "กำหนดการกระจาย" ในเมนู

จากนั้นคุณเลือกหนึ่งรายการจากจานสีของการแจกแจงที่ปรากฏขึ้น ซอฟต์แวร์ @RISK มีการกระจายมากกว่า 70 แบบให้เลือก ดังนั้นการเลือกอย่างใดอย่างหนึ่งอาจดูยากเกินไปในตอนแรก ด้านล่างนี้คือคำแนะนำบางส่วนที่ฉันใช้บ่อยที่สุด:

ปกติ. กำหนดโดยค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน นี่เป็นจุดเริ่มต้นที่ดีเนื่องจากความเรียบง่าย และเหมาะที่จะเป็นส่วนเสริมของแนวทาง Morningstar โดยที่คุณกำหนดการกระจายที่ครอบคลุมสถานการณ์หรือช่วงที่กำหนดไว้แล้วสำหรับอินพุตที่กำหนด ตรวจสอบให้แน่ใจว่าเคสมีความสมมาตรรอบเคสพื้นฐานและ ความน่าจะเป็นในแต่ละหางดูสมเหตุสมผล (พูด 25% ในตัวอย่าง Morningstar)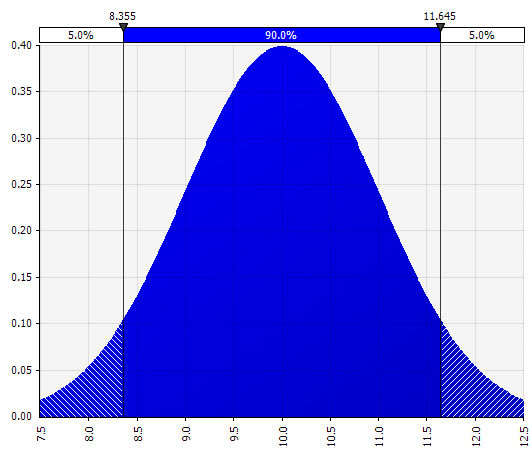
จอห์นสัน โมเมนต์ การเลือกสิ่งนี้ทำให้คุณสามารถกำหนดการกระจายและการแจกแจงแบบเบ้ด้วยหางที่หนาขึ้นหรือบางลง (โดยการเพิ่มพารามิเตอร์ความเบ้และความโด่งในทางเทคนิค) เบื้องหลังนี้ใช้อัลกอริธึมเพื่อเลือกหนึ่งในสี่การแจกแจงซึ่งสะท้อนถึงพารามิเตอร์ที่เลือกไว้สี่ตัว แต่ผู้ใช้จะมองไม่เห็นสิ่งนี้—ทั้งหมดที่เราต้องเน้นคือพารามิเตอร์ บางครั้ง ในกระบวนการรวบรวมข้อมูลสำหรับอินพุต จะเห็นชัดเจนว่าการแจกแจงแบบปกติไม่เหมาะสม ตัวอย่างเช่น สำหรับบริษัทที่อยู่ในช่วงต่ำสุดหรือสูงสุดของวัฏจักรอุตสาหกรรม ความน่าจะเป็นของผลการดำเนินงานที่ดีขึ้นหรือแย่ลงในอีกห้าปีข้างหน้าจะไม่มีความสมมาตร ยิ่งเข้าใกล้จุดสูงสุดมากเท่าไหร่ แนวโน้มขาลงก็จะยิ่งมีผลประกอบการที่แข็งแกร่งมากขึ้นเท่านั้น นี่คือจุดที่การกระจายแบบเบ้จะมีประโยชน์ มีการเขียนเกี่ยวกับแนวคิดของ "หางอ้วน" ในหลายด้านของการเงิน ดูเหมือนว่าการแจกแจงแบบปกติมักจะไม่ได้อธิบายผลลัพธ์ที่แท้จริงเป็นอย่างดี โดยมีเหตุการณ์ที่ไม่น่าจะเกิดขึ้นบ่อยมากเกินกว่าการแจกแจงแบบปกติจะระบุ
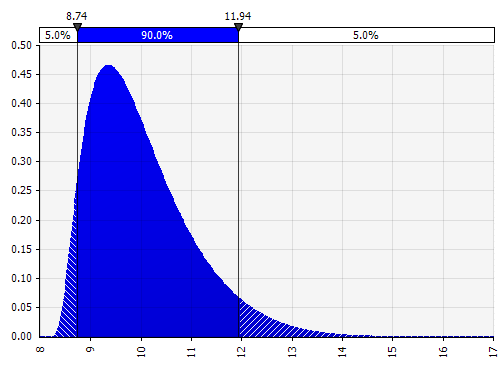ไม่ต่อเนื่อง เมื่อความน่าจะเป็นถูกกำหนดให้กับค่าเฉพาะตั้งแต่สองค่าขึ้นไป กลับไปที่ตัวอย่างโครงการ R&D ที่จัดฉากในตอนเริ่มต้น ความน่าจะเป็นของความสำเร็จในแต่ละขั้นตอนจะถูกจำลองเป็นการแจกแจงแบบไบนารีแบบไม่ต่อเนื่อง โดยผลลัพธ์ 1 แสดงถึงความสำเร็จและ 0 ความล้มเหลว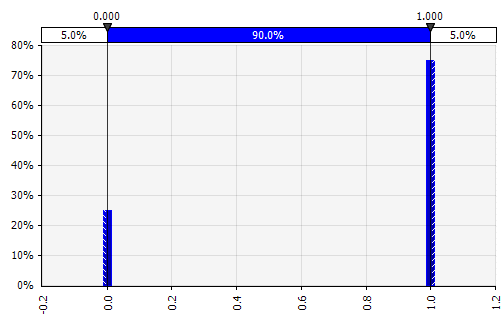
ข้อต่อกระจาย. เมื่อคุณมีจุดข้อมูลในอดีตจำนวนมาก ฟังก์ชันการกระจายที่เหมาะสมจะมีประโยชน์ นี่ไม่ได้หมายความว่าสามหรือสี่ปีของการเติบโตของยอดขายในอดีต แต่ข้อมูลอนุกรมเวลา เช่น ราคาสินค้าโภคภัณฑ์ อัตราแลกเปลี่ยนเงินตรา หรือราคาตลาดอื่นๆ ที่ประวัติศาสตร์สามารถให้ข้อมูลที่เป็นประโยชน์เกี่ยวกับแนวโน้มในอนาคตและระดับของความไม่แน่นอน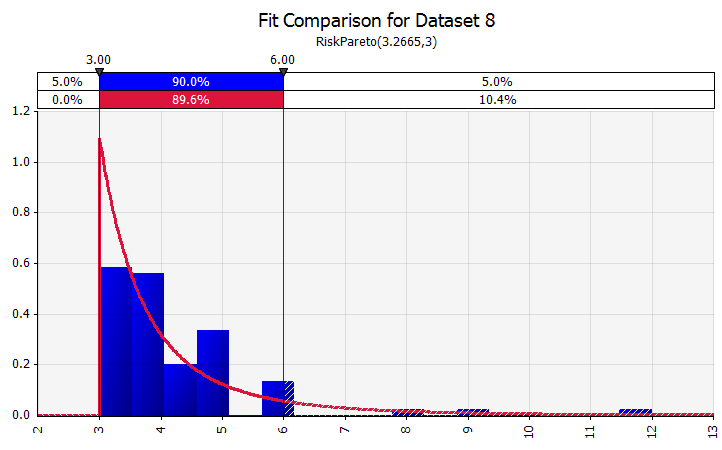
การรวมการแจกแจงที่แตกต่างกันหลายอย่างเข้าเป็นหนึ่งเดียว เพื่อลดผลกระทบที่อาจเกิดขึ้นจากอคติส่วนบุคคล มักจะเป็นความคิดที่ดีที่จะรวมข้อมูลจากแหล่งต่างๆ เข้าไว้ในสมมติฐาน และ/หรือทบทวนและอภิปรายข้อค้นพบ มีแนวทางที่แตกต่างกัน: 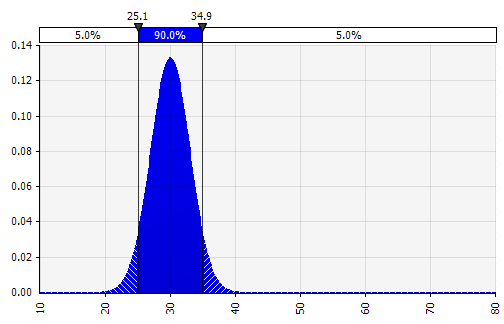เตรียมร่างหรือมุมมองแรกแล้วทบทวนกับผู้เชี่ยวชาญ ทีมผู้บริหารในวงกว้าง หรือผู้มีอำนาจตัดสินใจอื่นๆ พัฒนาการกระจายที่สำคัญที่สุดร่วมกันในการประชุม นี้สามารถนำไปสู่การอภิปรายที่ดีและผลลัพธ์ที่ดีขึ้น แต่เช่นเคยองค์ประกอบของกลุ่มเป็นสิ่งสำคัญ; การมีมุมมอง/หน้าที่ที่แตกต่างกันและส่งเสริมบรรยากาศของการอภิปรายที่มีพลังแต่ให้เกียรติ แน่นอนว่ามีประโยชน์ พัฒนาหนึ่งการแจกจ่ายสำหรับแหล่งข่าวสำคัญแต่ละแหล่ง และรวมเข้าด้วยกัน โดยให้น้ำหนักตามศรัทธาที่คุณมีในแต่ละแหล่ง หากได้รับข้อมูลจากผู้เชี่ยวชาญหลายคน อาจเป็นความคิดที่ดีที่จะให้แต่ละคนแสดงความเห็นของตนเอง โดยไม่ขึ้นกับคนอื่นๆ แล้วจึงรวมเป็นหนึ่งเดียว ฟังก์ชัน @RISK MakeRiskInput ทำเพื่อเรา	น้ำหนัก: 20% 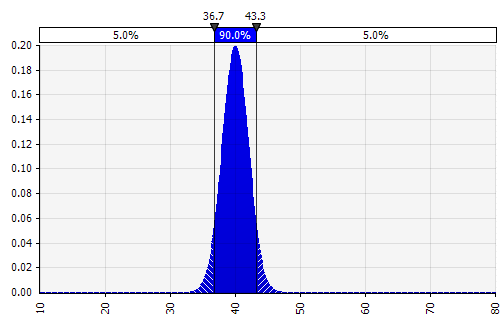+ น้ำหนัก: 20% 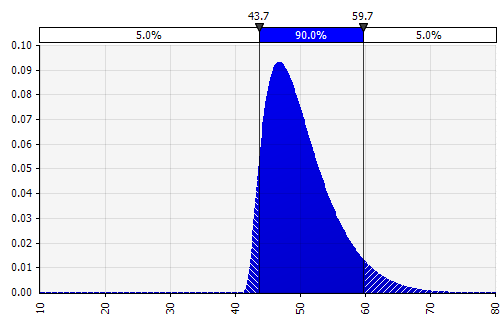+ น้ำหนัก: 60% =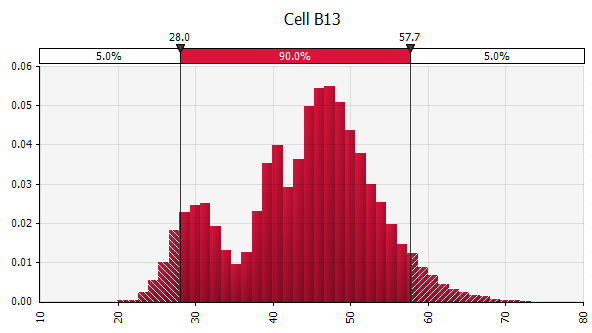
ด้วยมือเปล่า เพื่อแสดงตัวอย่างการแจกจ่ายอย่างรวดเร็วโดยเป็นส่วนหนึ่งของการสนทนา หรือถ้าคุณต้องการการแจกจ่ายเมื่อร่างแบบจำลองที่สร้างได้ยากจากจานสีที่มีอยู่ ฟังก์ชันการทำงานด้วยมือเปล่าก็มีประโยชน์ ตามความหมายของชื่อ สิ่งนี้ทำให้คุณสามารถวาดการกระจายโดยใช้เครื่องมือระบายสีอย่างง่าย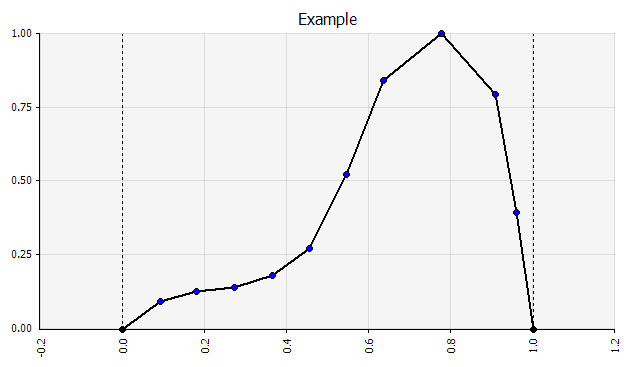

ตอนนี้เราเห็นการแสดงภาพของการแจกแจง โดยมีพารามิเตอร์สองสามตัวทางด้านซ้ายมือ สัญลักษณ์ค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานควรดูคุ้นเคย ในกรณีของการแจกแจงแบบปกติ ค่าเฉลี่ยจะเท่ากับค่าที่เราป้อนก่อนหน้านี้เป็นค่าเดียวในเซลล์ นี่คือตัวอย่างการกระจายความน่าจะเป็นในการขายในปี 2018 โดย 10% แสดงถึงค่าเฉลี่ย ในขณะที่โมเดลทั่วไปของคุณจะเน้นที่ตัวเลข 10% เท่านั้น หรือมีสถานการณ์ "กระทิง" และ "หมี" ที่อาจมีการเติบโต 15% และ 5% ตามลำดับ ตอนนี้ให้ข้อมูลเกี่ยวกับผลลัพธ์ที่คาดหวังอย่างเต็มรูปแบบ

ประโยชน์อย่างหนึ่งของการจำลองแบบมอนติคาร์โลคือผลลัพธ์ด้านท้ายความน่าจะเป็นต่ำสามารถกระตุ้นการคิดและการอภิปรายได้ เฉพาะการแสดงสถานการณ์กลับหัวและขาลงเท่านั้นที่สามารถทำให้เกิดความเสี่ยงที่ผู้มีอำนาจตัดสินใจตีความว่าเป็นขอบเขตภายนอก โดยไม่สนใจสถานการณ์ที่อยู่ภายนอก ซึ่งอาจส่งผลให้มีข้อบกพร่องในการตัดสินใจ โดยการเปิดเผยผลลัพธ์ที่อยู่นอกเหนือการยอมรับความเสี่ยงขององค์กรหรือบุคคล แม้แต่ความน่าจะเป็น 5% หรือ 1% อาจไม่เป็นที่ยอมรับหากสถานการณ์ที่เป็นปัญหาจะส่งผลร้ายแรง

ขั้นตอนที่ 3 ขยายการพยากรณ์รายได้จากหนึ่งปีเป็นหลาย ๆ

ด้วยการสร้างแบบจำลองมอนติคาร์โล ให้คำนึงถึงว่าการกระจายความไม่แน่นอนและความน่าจะเป็นซ้อนกันอย่างไร เช่น เมื่อเวลาผ่านไป มาทบทวนตัวอย่างกัน เนื่องจากยอดขายในแต่ละปีขึ้นอยู่กับการเติบโตในช่วงก่อนหน้า เราจึงสามารถเห็นภาพและเห็นว่ายอดขายประมาณการในปี 2022 ของเรามีความไม่แน่นอนมากกว่าในปี 2018 (แสดงโดยใช้ส่วนเบี่ยงเบนมาตรฐานและช่วงความเชื่อมั่น 95% ในแต่ละปี) เพื่อความง่าย ตัวอย่างด้านล่างระบุการเติบโตเป็นเวลาหนึ่งปี 2018 จากนั้นจึงนำอัตราการเติบโตแบบเดียวกันนั้นไปใช้กับแต่ละปีถัดไปจนถึงปี 2022 อีกวิธีหนึ่งคือต้องมีการแจกแจงอิสระห้าครั้ง หนึ่งครั้งต่อปี

ขั้นตอนที่ 4 ดำเนินการต่อในงบกำไรขาดทุน - การแสดงส่วนต่างเป็นการกระจายความน่าจะเป็น

ตอนนี้เราประมาณการการกระจายความน่าจะเป็นสำหรับ EBIT Margin ในปี 2018 (เน้นที่ด้านล่าง) แบบเดียวกับที่เราทำเพื่อการเติบโตของยอดขาย

ในที่นี้ เราสามารถใช้ฟังก์ชันสหสัมพันธ์เพื่อจำลองสถานการณ์ที่มีความสัมพันธ์ที่ชัดเจนระหว่างส่วนแบ่งการตลาดและความสามารถในการทำกำไร ซึ่งสะท้อนถึงการประหยัดจากขนาด สถานการณ์จำลองที่มีการเติบโตของยอดขายสูงขึ้นเมื่อเทียบกับตลาดและส่วนแบ่งการตลาดที่สัมพันธ์กันที่สูงขึ้นตามลำดับสามารถจำลองให้มีความสัมพันธ์เชิงบวกกับอัตรากำไร EBIT ที่สูงขึ้นได้ ในอุตสาหกรรมที่โชคลาภของบริษัทมีความสัมพันธ์อย่างมากกับปัจจัยภายนอกอื่นๆ เช่น ราคาน้ำมันหรืออัตราแลกเปลี่ยนเงินตราต่างประเทศ การกำหนดการกระจายสำหรับปัจจัยนั้นและการสร้างแบบจำลองความสัมพันธ์กับยอดขายและความสามารถในการทำกำไร

ขึ้นอยู่กับเวลาที่มีอยู่ ขนาดของธุรกรรม และปัจจัยอื่นๆ มักจะเหมาะสมที่จะสร้างแบบจำลองการดำเนินงานและป้อนตัวแปรที่ไม่แน่นอนที่สุดอย่างชัดเจน ซึ่งรวมถึงปริมาณและราคาของผลิตภัณฑ์ ราคาสินค้าโภคภัณฑ์ อัตรา FX รายการค่าใช้จ่ายหลัก ผู้ใช้งานรายเดือน และรายได้เฉลี่ยต่อหน่วย (ARPU) นอกจากนี้ยังเป็นไปได้ที่จะสร้างแบบจำลองนอกเหนือจากตัวแปรปริมาณ เช่น เวลาในการพัฒนา เวลาสู่ตลาด หรืออัตราการยอมรับของตลาด

ขั้นตอนที่ 5. งบดุลและงบกระแสเงินสด

เมื่อใช้แนวทางที่สรุปไว้ ตอนนี้เราสามารถดำเนินการผ่านงบดุลและงบกระแสเงินสด โดยใส่สมมติฐานและใช้การแจกแจงความน่าจะเป็นตามที่เห็นสมควร

หมายเหตุเกี่ยวกับรายจ่ายรายจ่าย: สามารถสร้างแบบจำลองได้ทั้งในจำนวนที่แน่นอนหรือเป็นเปอร์เซ็นต์ของยอดขาย โดยอาจใช้ร่วมกับการลงทุนแบบทีละขั้นที่มากขึ้น ตัวอย่างเช่น โรงงานผลิตอาจมีขีดจำกัดกำลังการผลิตที่ชัดเจนและการลงทุนขยายขนาดใหญ่หรือโรงงานใหม่ที่จำเป็นเมื่อยอดขายเกินเกณฑ์ เนื่องจากการทำซ้ำ 1,000 หรือ 10,000 ครั้งในแต่ละครั้งจะเป็นการคำนวณใหม่ของแบบจำลองทั้งหมด จึงสามารถใช้สูตรง่ายๆ ที่เรียกต้นทุนการลงทุนได้หาก/เมื่อถึงปริมาณที่กำหนด

ขั้นตอนที่ 6 การสิ้นสุดแบบจำลอง

การสร้างแบบจำลองมอนติคาร์โลมีขั้นตอนเพิ่มเติมหนึ่งขั้นตอนเมื่อเทียบกับแบบจำลองทางการเงินมาตรฐาน: เซลล์ที่เราต้องการประเมินผลลัพธ์จำเป็นต้องกำหนดเป็นเซลล์ผลลัพธ์โดยเฉพาะ ซอฟต์แวร์จะบันทึกผลลัพธ์ของการทำซ้ำแต่ละครั้งของการจำลองสำหรับเซลล์เหล่านั้นเพื่อให้เราประเมินหลังจากการจำลองเสร็จสิ้น เซลล์ทั้งหมดในแบบจำลองทั้งหมดจะถูกคำนวณใหม่ด้วยการวนซ้ำแต่ละครั้ง แต่ผลลัพธ์ของการวนซ้ำในเซลล์อื่นซึ่งไม่ได้ถูกกำหนดให้เป็นเซลล์อินพุตหรือเอาต์พุต จะสูญหายไปและไม่สามารถวิเคราะห์ได้หลังจากการจำลองเสร็จสิ้น ดังที่คุณเห็นในภาพหน้าจอด้านล่าง เรากำหนดให้เซลล์ผลลัพธ์ MIRR เป็นเซลล์ผลลัพธ์

เมื่อคุณสร้างแบบจำลองเสร็จแล้ว ก็ถึงเวลาเรียกใช้การจำลองเป็นครั้งแรกโดยเพียงแค่กด "เริ่มการจำลอง" แล้วรอสักครู่

ขั้นตอนที่ 7 การตีความผลลัพธ์

ผลลัพธ์ที่แสดงเป็นความน่าจะเป็น ในขณะที่แบบจำลองของเราก่อนหน้านี้ให้ค่าเดียวสำหรับ IRR ที่แก้ไขแล้ว ตอนนี้เราสามารถเห็นได้อย่างชัดเจนว่ามีหลายผลลัพธ์ที่เป็นไปได้รอบๆ ค่านั้น โดยมีความน่าจะเป็นต่างกัน ซึ่งช่วยให้เราสามารถใช้ประโยคคำถามใหม่ได้ เช่น "การลงทุนนี้จะมีอัตราผลตอบแทนจากอุปสรรคไหม" กับ “มีแนวโน้มว่าเราจะตีหรือเกินอัตราอุปสรรค์ของเราได้อย่างไร” คุณสามารถสำรวจผลลัพธ์ที่น่าจะใช้มากที่สุด ตัวอย่างเช่น ช่วงความมั่นใจ การแสดงภาพข้อมูลมีประโยชน์เมื่อสื่อสารผลลัพธ์ไปยังผู้มีส่วนได้ส่วนเสียที่แตกต่างกัน และคุณสามารถซ้อนทับผลลัพธ์จากธุรกรรมอื่น ๆ เพื่อเปรียบเทียบภาพว่าน่าสนใจเพียงใดและ (ไม่) บางส่วนในปัจจุบันเปรียบเทียบกับผู้อื่น (ดูด้านล่าง)

การทำความเข้าใจระดับของความไม่แน่นอนในผลลัพธ์สุดท้าย หากเราสร้างแผนภูมิความผันแปรของกระแสเงินสดเมื่อเวลาผ่านไป คล้ายกับที่เราทำในตอนแรกสำหรับการขาย จะเห็นได้ชัดว่าความแปรปรวนของกระแสเงินสดอิสระมีนัยสำคัญ แม้ว่าจะมีความไม่แน่นอนค่อนข้างน้อยในการขายและปัจจัยการผลิตอื่นๆ ที่เราจำลองเป็นการแจกแจงความน่าจะเป็น โดยมีผลลัพธ์ตั้งแต่ประมาณ 0.5 ล้านยูโรถึง 5.0 ล้านยูโร—เพิ่มขึ้นเป็น 10 เท่า—แม้แต่ค่าเบี่ยงเบนมาตรฐานเพียงค่าเดียวจากค่าเฉลี่ย นี่เป็นผลมาจากการซ้อนสมมติฐานที่ไม่แน่นอนทับกัน ซึ่งเป็นผลที่ประกอบขึ้นจาก "แนวตั้ง" ในช่วงหลายปีที่ผ่านมา และ "ในแนวนอน" ลงในงบการเงิน การแสดงภาพให้ข้อมูลเกี่ยวกับความไม่แน่นอนทั้งสองประเภท

การวิเคราะห์ความไว: แนะนำกราฟพายุทอร์นาโด ประเด็นสำคัญอีกประการหนึ่งคือการทำความเข้าใจว่าปัจจัยการผลิตใดมีผลกระทบต่อผลลัพธ์สุดท้ายของคุณมากที่สุด ตัวอย่างคลาสสิกคือความสำคัญของอัตราคิดลดหรือสมมติฐานมูลค่าเทอร์มินัลมักให้น้ำหนักน้อยเกินไปเมื่อเทียบกับการคาดการณ์กระแสเงินสด วิธีหนึ่งที่ใช้กันทั่วไปในการจัดการสิ่งนี้คือการใช้เมทริกซ์ที่คุณใส่คีย์อินพุตหนึ่งอันในแต่ละแกน แล้วคำนวณผลลัพธ์ในแต่ละเซลล์ (ดูด้านล่าง) สิ่งนี้มีประโยชน์โดยเฉพาะอย่างยิ่งในสถานการณ์ที่การตัดสินใจขึ้นอยู่กับสมมติฐานหลักหนึ่งข้อหรือสองสามข้อ - ในสถานการณ์ "สิ่งที่คุณต้องเชื่อ" เหล่านี้ ผู้มีอำนาจตัดสินใจ (เช่น) คณะกรรมการการลงทุนหรือทีมผู้บริหารระดับสูงอาจมีมุมมองที่แตกต่างกัน สมมติฐานหลักเหล่านั้น และเมทริกซ์ดังที่กล่าวมาข้างต้น ทำให้แต่ละข้อสามารถค้นหาค่าผลลัพธ์ที่สอดคล้องกับมุมมองของพวกเขา และสามารถตัดสินใจ โหวต หรือให้คำแนะนำตามนั้น

ปรับปรุงด้วยการจำลอง Monte Carlo เมื่อใช้การจำลองแบบมอนติคาร์โล วิธีการนั้นสามารถเสริมด้วยวิธีการอื่น: แผนภาพพายุทอร์นาโด การแสดงภาพข้อมูลนี้แสดงรายการอินพุตและสมมติฐานที่ไม่แน่นอนที่แตกต่างกันบนแกนตั้ง แล้วแสดงให้เห็นว่าผลกระทบของแต่ละรายการมีมากเพียงใดในผลลัพธ์สุดท้าย

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein