Toolbox di Forecaster: come eseguire simulazioni Monte Carlo

Sintesi

introduzione

In primo luogo, l'unica certezza è che non c'è certezza. In secondo luogo, ogni decisione di conseguenza è una questione di ponderazione delle probabilità. Terzo, nonostante l'incertezza dobbiamo decidere e dobbiamo agire. E infine dobbiamo giudicare le decisioni non solo sui risultati, ma anche su come sono state prese. – Robert E. Rubin

Uno degli aspetti più importanti e stimolanti della previsione è gestire l'incertezza inerente all'esame del futuro. Avendo costruito e popolato centinaia di modelli finanziari e operativi per LBO, raccolte fondi per startup, budget, fusioni e acquisizioni e piani strategici aziendali dal 2003, ho assistito a un'ampia gamma di approcci per farlo. Ogni CEO, CFO, membro del consiglio, investitore o membro del comitato di investimento porta la propria esperienza e il proprio approccio alle proiezioni finanziarie e all'incertezza, influenzati da diversi incentivi. Spesso, confrontare i risultati effettivi con le proiezioni fornisce un apprezzamento di quanto possano essere grandi le deviazioni tra previsioni e risultati effettivi, e quindi la necessità di comprendere e riconoscere esplicitamente l'incertezza.

Inizialmente ho iniziato a utilizzare analisi di scenario e di sensibilità per modellare l'incertezza e continuo a considerarle strumenti molto utili. Da quando ho aggiunto le simulazioni Monte Carlo alla mia cassetta degli attrezzi nel 2010, ho scoperto che sono uno strumento estremamente efficace per perfezionare e migliorare il modo in cui pensi al rischio e alle probabilità. Ho utilizzato l'approccio per qualsiasi cosa, dalla costruzione di valutazioni DCF, alla valutazione delle opzioni call in M&A e alla discussione dei rischi con i prestatori alla ricerca di finanziamenti e alla guida dell'allocazione dei finanziamenti VC per le startup. L'approccio è sempre stato ben accolto dai membri del consiglio di amministrazione, dagli investitori e dai team dirigenziali. In questo articolo, fornisco un tutorial passo dopo passo sull'utilizzo pratico delle simulazioni Monte Carlo costruendo un modello di valutazione DCF.

Ogni decisione è una questione di probabilità di pesare

Prima di iniziare con il caso di studio, esaminiamo alcuni approcci diversi per gestire l'incertezza. Il concetto di valore atteso , la media ponderata per la probabilità dei flussi di cassa in tutti i possibili scenari, è Finance 101. Ma i professionisti della finanza, e più in generale i decisori, adottano approcci molto diversi quando traducono in pratica questa semplice intuizione. L'approccio può variare dal semplice non riconoscere o discutere l'incertezza, da un lato, a modelli e software sofisticati dall'altro. In alcuni casi, le persone finiscono per passare più tempo a discutere di probabilità che a calcolare i flussi di cassa.

Oltre a non affrontarlo semplicemente, esaminiamo alcuni modi per gestire l'incertezza nelle proiezioni a medio o lungo termine. Molti di questi dovrebbero esserti familiari.

Creazione di uno scenario. Questo approccio è l'impostazione predefinita per budget, molte startup e persino decisioni di investimento. Oltre a non contenere alcuna informazione sul grado di incertezza o sul riconoscimento che i risultati possono differire dalle proiezioni, può essere ambiguo ed essere interpretato in modo diverso a seconda dello stakeholder. Alcuni potrebbero interpretarlo come un obiettivo elastico, in cui è più probabile che il risultato effettivo non sia inferiore che superiore. Alcuni la vedono come una performance di base con più vantaggi che svantaggi. Altri potrebbero vederlo come un "caso base" con probabilità 50/50 su e giù. In alcuni approcci, specialmente per le startup, è molto ambizioso e il fallimento o il deficit è di gran lunga il risultato più probabile, ma nel tentativo di tenere conto del rischio viene utilizzato un tasso di sconto più elevato.	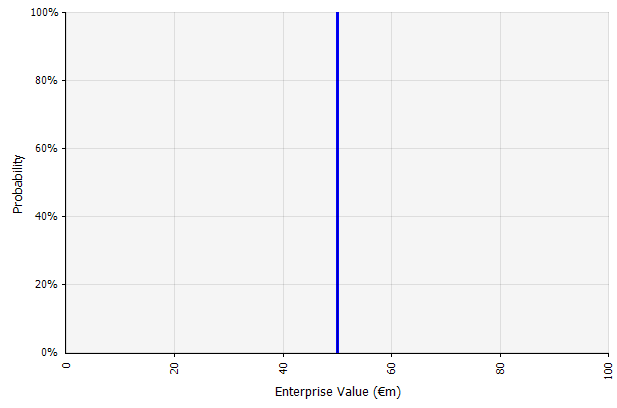Gli input nella previsione dei flussi di cassa a lungo termine secondo questo approccio sono tutti stime puntuali, che in questo esempio producono un risultato puntuale di 50 milioni di euro, con una probabilità implicita del 100%.
Creazione di più scenari. Questo approccio riconosce che è improbabile che la realtà si svolga secondo un unico piano dato. 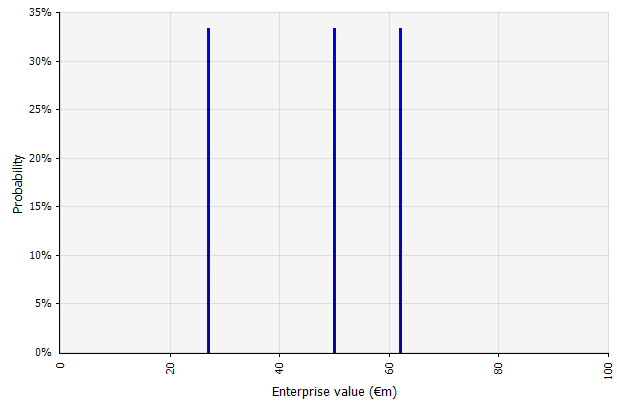Nella sua forma più semplice, l'analisi di sensitività, potrebbe simulare l'impatto, ad esempio, di una crescita delle vendite del 10% al di sopra e al di sotto di quella del caso base, utilizzando un dato mix di costi fissi, semivariabili e variabili per stimare il risultato finale impatto. In forme più complesse si pensa al futuro da una prospettiva completamente diversa per ogni scenario e si analizza l'impatto che i diversi sviluppi tecnologici, le dinamiche competitive e le macro tendenze avranno sulle prestazioni dell'azienda. Spesso, sfortunatamente, gli scenari vengono scelti in modo abbastanza arbitrario e talvolta con un risultato finale desiderato in mente.	I tre diversi scenari producono tre diversi risultati, qui assunti ugualmente probabili. Le probabilità di esiti al di fuori degli scenari alto e basso non vengono considerate.
Creazione di casi base, al rialzo e al ribasso con probabilità esplicitamente riconosciute. Cioè, i casi orso e rialzo contengono, ad esempio, una probabilità del 25% in ciascuna coda e la stima del valore equo rappresenta il punto medio. Un utile vantaggio di ciò dal punto di vista della gestione del rischio è l'analisi esplicita del rischio di coda, ovvero eventi al di fuori degli scenari di rialzo e di ribasso.	Illustrazione tratta dal Manuale di valutazione Morningstar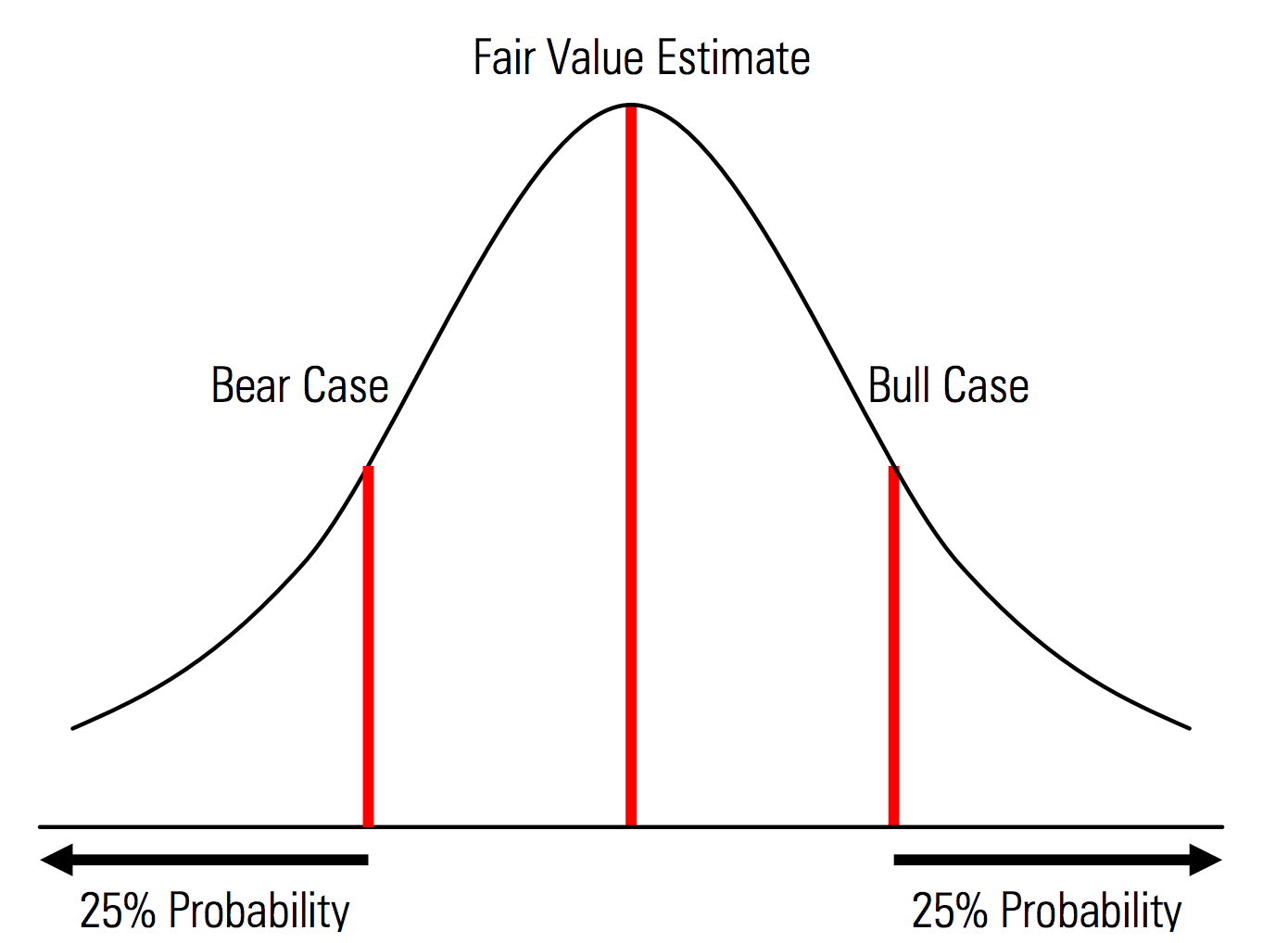
Utilizzo di distribuzioni di probabilità e simulazioni Monte Carlo. L'uso delle distribuzioni di probabilità consente di modellare e visualizzare l'intera gamma di possibili risultati nella previsione. Questo può essere fatto non solo a livello aggregato, ma anche per singoli input, ipotesi e fattori determinanti dettagliati. I metodi Monte Carlo vengono quindi utilizzati per calcolare le distribuzioni di probabilità risultanti a livello aggregato, consentendo l'analisi di come diverse variabili incerte contribuiscono all'incertezza dei risultati complessivi. Forse la cosa più importante, l'approccio costringe tutti coloro che sono coinvolti nell'analisi e nella decisione a riconoscere esplicitamente l'incertezza insita nella previsione ea pensare in base alle probabilità. Proprio come gli altri approcci, questo ha i suoi svantaggi, incluso il rischio di falsa precisione e conseguente eccessiva sicurezza che potrebbe derivare dall'uso di un modello più sofisticato, e il lavoro aggiuntivo necessario per selezionare distribuzioni di probabilità adeguate e stimare i loro parametri dove altrimenti sarebbero solo stime puntuali Usato.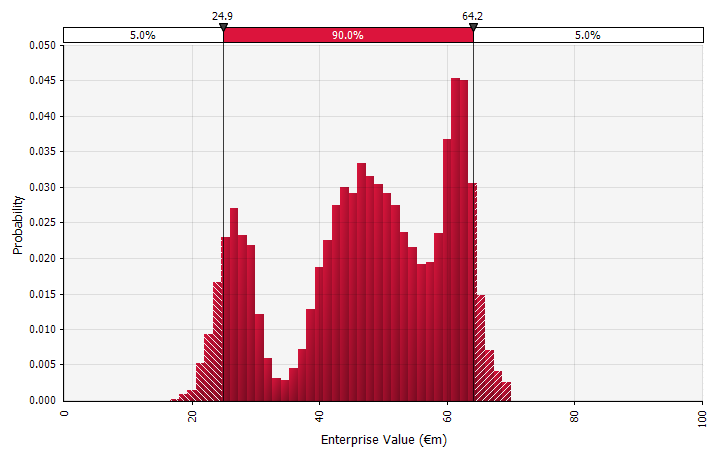

Che cos'è una simulazione Monte Carlo?

Le simulazioni Monte Carlo modellano la probabilità di risultati diversi nelle previsioni e nelle stime finanziarie. Si guadagnano il nome dalla zona di Monte Carlo a Monaco, famosa in tutto il mondo per i suoi casinò di fascia alta; i risultati casuali sono centrali nella tecnica, proprio come lo sono per la roulette e le slot machine. Le simulazioni Monte Carlo sono utili in un'ampia gamma di campi, tra cui ingegneria, gestione di progetti, esplorazione di petrolio e gas e altri settori ad alta intensità di capitale, ricerca e sviluppo e assicurazioni; qui, mi concentro sulle applicazioni in finanza e affari.

Distribuzioni di probabilità

Nella simulazione, gli input incerti sono descritti utilizzando distribuzioni di probabilità, descritte da parametri quali media e deviazione standard. Esempi di input nelle proiezioni finanziarie potrebbero essere qualsiasi cosa, da entrate e margini a qualcosa di più granulare, come i prezzi delle materie prime, le spese in conto capitale per un'espansione o i tassi di cambio.

Quando uno o più input sono descritti come distribuzioni di probabilità, l'output diventa anche una distribuzione di probabilità. Un computer estrae casualmente un numero da ciascuna distribuzione di input e calcola e salva il risultato. Questo viene ripetuto centinaia, migliaia o decine di migliaia di volte, ciascuna chiamata iterazione. Se presi insieme, queste iterazioni approssimano la distribuzione di probabilità del risultato finale.

Tipi di ingressi

Le distribuzioni di input possono essere continue , in cui il valore generato casualmente può assumere qualsiasi valore sotto la distribuzione (ad esempio una distribuzione normale) o discrete , in cui le probabilità sono associate a due o più scenari distinti.

Una simulazione può anche contenere un mix di distribuzioni di diversi tipi. Prendi, ad esempio, un progetto di ricerca e sviluppo farmaceutico con diverse fasi, ciascuna con una discreta probabilità di successo o fallimento. Questo può essere combinato con distribuzioni continue che descrivono importi di investimento incerti necessari per ciascuna fase e potenziali ricavi se il progetto si traduce in un prodotto che raggiunge il mercato. Il grafico seguente mostra l'output di tale simulazione: una probabilità del 65% circa di perdere l'intero investimento da 5 milioni di euro a 50 milioni di euro (valore attuale) e una probabilità del 35% circa di un guadagno netto molto probabilmente nell'intervallo di Da € 100 a € 250: informazioni che andrebbero perse se le metriche di output chiave come MIRR o NPV fossero mostrate come stime puntuali anziché come distribuzioni di probabilità.

Simulazioni Monte Carlo in pratica

Uno dei motivi per cui le simulazioni Monte Carlo non sono più ampiamente utilizzate è perché i tipici strumenti finanziari quotidiani non le supportano molto bene. Excel e Fogli Google contengono un numero o un risultato di formula in ogni cella e, sebbene possano definire distribuzioni di probabilità e generare numeri casuali, costruire da zero un modello finanziario con funzionalità Monte Carlo è ingombrante. E, sebbene molte istituzioni finanziarie e società di investimento utilizzino simulazioni Monte Carlo per valutare derivati, analizzare portafogli e altro, i loro strumenti sono in genere sviluppati internamente, proprietari o proibitivamente costosi, rendendoli inaccessibili al singolo professionista della finanza.

Pertanto, voglio attirare l'attenzione sui plug-in di Excel come @RISK di Palisade, ModelRisk di Vose e RiskAMP, che semplificano notevolmente il lavoro con le simulazioni Monte Carlo e consentono di integrarle nei modelli esistenti. Nella procedura dettagliata seguente, userò @RISK.

Caso di studio: proiezioni del flusso di cassa con simulazione Monte Carlo

Esaminiamo un semplice esempio che illustra i concetti chiave di una simulazione Monte Carlo: una previsione del flusso di cassa a cinque anni. In questa procedura dettagliata, ho impostato e popolato un modello di flusso di cassa di base per scopi di valutazione, ho sostituito gradualmente gli input con distribuzioni di probabilità e, infine, ho eseguito la simulazione e analizzato i risultati.

Passaggio 1. Scelta o costruzione del modello

Per iniziare, utilizzo un modello semplice, incentrato sull'evidenziazione delle caratteristiche chiave dell'utilizzo delle distribuzioni di probabilità. Si noti che, per cominciare, questo modello non è diverso da qualsiasi altro modello di Excel; i plugin che ho menzionato sopra funzionano con i tuoi modelli e fogli di calcolo esistenti. Il modello seguente è una semplice versione standard popolata con ipotesi per formare uno scenario.

Passaggio 2. Creazione della prima distribuzione di probabilità

Innanzitutto, dobbiamo raccogliere le informazioni necessarie per formulare le nostre ipotesi, quindi dobbiamo scegliere le corrette distribuzioni di probabilità da inserire. È importante notare che la fonte degli input/presupposti chiave è la stessa indipendentemente dall'approccio adottato per gestire l'incertezza. La due diligence commerciale, una revisione completa del piano aziendale dell'azienda nel contesto dello sviluppo del mercato previsto, delle tendenze del settore e delle dinamiche competitive, include in genere l'estrapolazione da dati storici, l'incorporazione dell'opinione di esperti, lo svolgimento di ricerche di mercato e il colloquio con i partecipanti al mercato. In base alla mia esperienza, esperti e partecipanti al mercato sono felici di discutere diversi scenari, rischi e gamme di risultati. Tuttavia, la maggior parte non descrive esplicitamente le distribuzioni di probabilità.

Esaminiamo ora e sostituiamo i nostri valori di input chiave con le distribuzioni di probabilità uno per uno, iniziando con la crescita stimata delle vendite per il primo anno di previsione (2018). Il plug-in @RISK per Excel può essere valutato con una prova gratuita di 15 giorni in modo da poterlo scaricare dal sito Web di Palisade e installarlo con pochi clic. Con il plug-in @RISK abilitato, seleziona la cella in cui desideri distribuire la distribuzione e seleziona "Definisci distribuzione" nel menu.

Quindi ne selezioni uno dalla tavolozza delle distribuzioni che viene visualizzata. Il software @RISK offre più di 70 diverse distribuzioni tra cui scegliere, quindi sceglierne una può sembrare all'inizio opprimente. Di seguito è una guida per una manciata che uso più spesso:

Normale. Definito da media e deviazione standard. Questo è un buon punto di partenza per la sua semplicità e adatto come estensione all'approccio Morningstar, in cui si definisce una distribuzione che copre scenari o intervalli forse già definiti per un dato input, assicurando che i casi siano simmetrici rispetto al caso base e che le probabilità in ciascuna coda appaiano ragionevoli (diciamo 25% come nell'esempio Morningstar).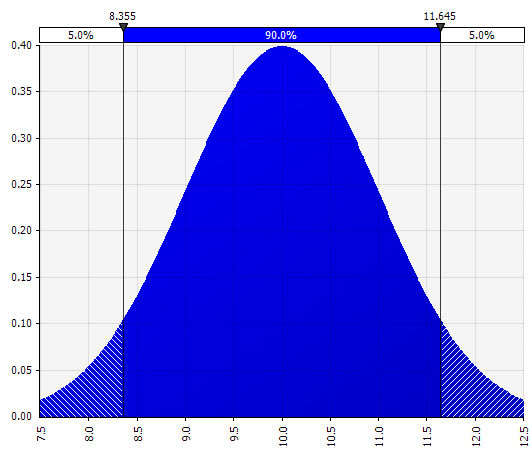
Momenti Johnson. La scelta di questa opzione consente di definire distribuzioni asimmetriche e distribuzioni con code più grasse o più sottili (aggiungendo tecnicamente parametri di asimmetria e curtosi). Dietro le quinte, questo utilizza un algoritmo per scegliere una delle quattro distribuzioni che riflette i quattro parametri scelti, ma che è invisibile all'utente: tutto ciò su cui dobbiamo concentrarci sono i parametri. A volte, nel processo di raccolta delle informazioni per l'input, diventa chiaro che la distribuzione normale non è appropriata. Ad esempio, per un'azienda al minimo o al culmine di un ciclo industriale, le probabilità di prestazioni migliori o peggiori nei prossimi, ad esempio, cinque anni non saranno simmetriche. Più ci si avvicina al picco, più è probabile una flessione rispetto al proseguimento della forte performance. È qui che può essere utile una distribuzione asimmetrica. Molto è stato scritto sul concetto di "coda grassa" in molte aree della finanza. Sembra che la distribuzione normale spesso non descriva molto bene i risultati effettivi, con eventi che dovrebbero essere molto rari che si verificano più frequentemente di quanto indicherebbe una distribuzione normale.
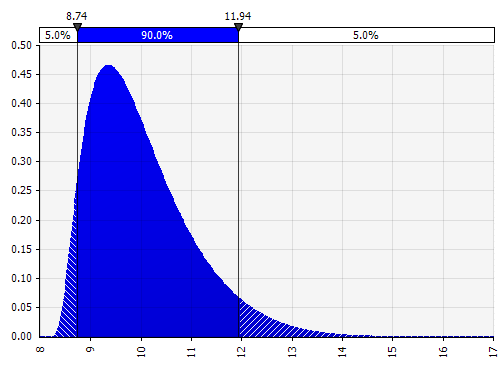Discreto. Dove le probabilità sono date a due o più valori specifici. Tornando all'esempio del progetto di ricerca e sviluppo in fasi all'inizio, la probabilità di successo in ogni fase è modellata come una distribuzione binaria discreta, con un risultato di 1 che rappresenta il successo e 0 di fallimento.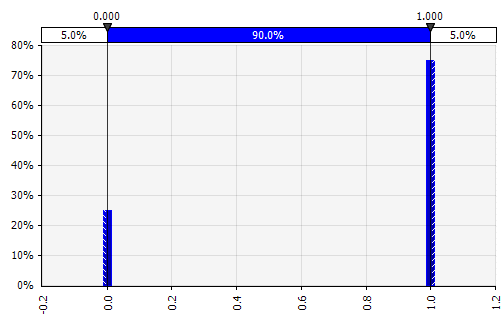
Raccordo di distribuzione. Quando si dispone di una grande quantità di punti dati storici, la funzionalità di adattamento della distribuzione è utile. Ciò non significa, ad esempio, tre o quattro anni di crescita storica delle vendite, ma dati di serie temporali come i prezzi delle materie prime, i tassi di cambio delle valute o altri prezzi di mercato in cui la cronologia può fornire informazioni utili sulle tendenze future e sul grado di incertezza.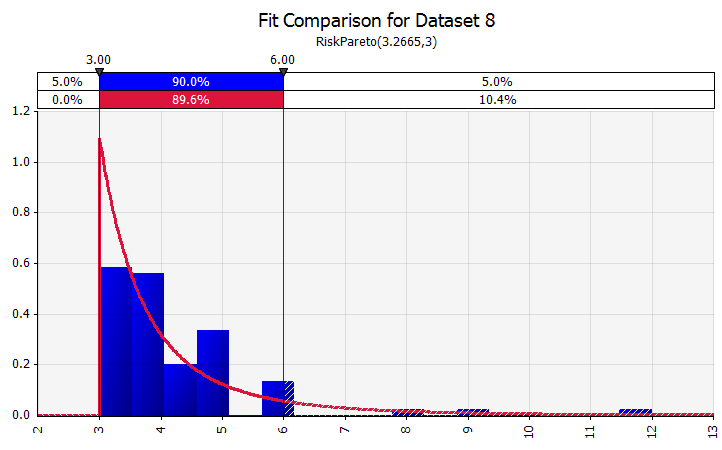
Combinando diverse distribuzioni diverse in una. Per mitigare il potenziale impatto dei pregiudizi individuali, è spesso una buona idea incorporare l'input di diverse fonti in un'ipotesi e/o rivedere e discutere i risultati. Esistono diversi approcci: 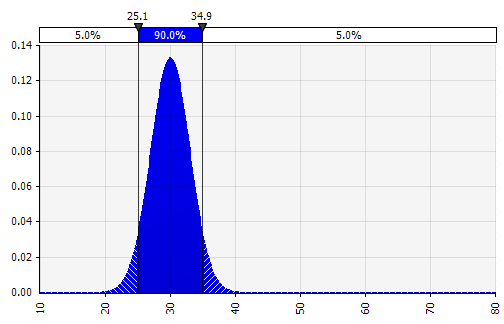Preparare una bozza o una prima vista e poi rivederla con gli esperti, il team di gestione più ampio o altri responsabili delle decisioni. Sviluppare le distribuzioni più importanti insieme in una riunione. Questo può portare a una buona discussione e a risultati migliori, ma come sempre la composizione del gruppo è fondamentale; avere diverse prospettive/funzioni rappresentate e promuovere un'atmosfera di dibattito vigoroso ma rispettoso è ovviamente utile. Sviluppa una distribuzione per ciascuna fonte chiave e combinale, ponderate in base a quanta fiducia hai in ciascuna. Se ricevi input da diversi esperti, può essere una buona idea lasciare che ciascuno di essi fornisca il proprio punto di vista, indipendentemente dagli altri, e poi unirli in uno solo. La funzione @RISK MakeRiskInput fa questo per noi.	Peso: 20% 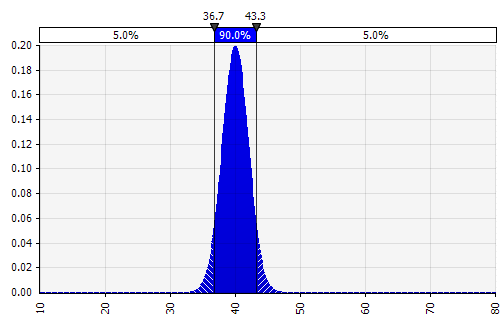+ Peso: 20% 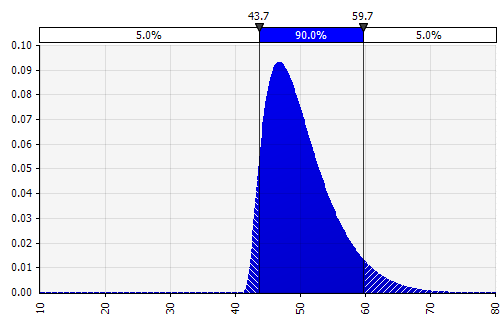+ Peso: 60% =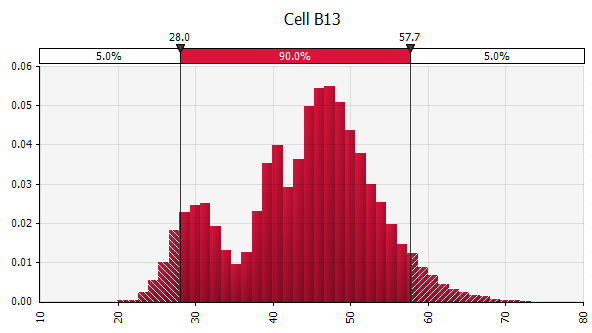
A mano libera. Per illustrare rapidamente una distribuzione come parte di discussioni o se è necessaria una distribuzione durante la stesura di un modello non facilmente creato dalla tavolozza esistente, la funzionalità a mano libera è utile. Come suggerisce il nome, questo ti consente di disegnare la distribuzione utilizzando un semplice strumento di pittura.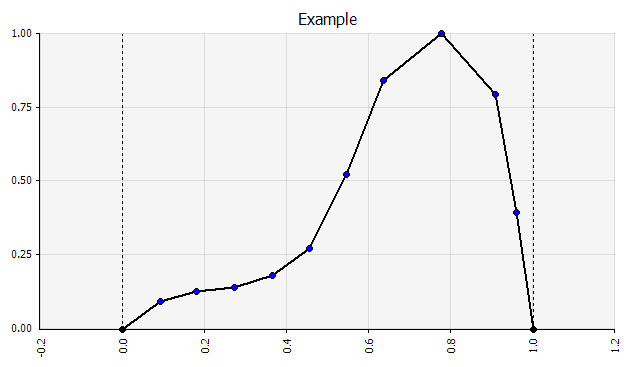

Ora vediamo una visualizzazione della distribuzione, con alcuni parametri sul lato sinistro. I simboli della media e della deviazione standard dovrebbero sembrare familiari. Nel caso di una distribuzione normale, la media sarebbe quella che abbiamo precedentemente inserito come valore singolo nella cella. Ecco la distribuzione della probabilità di vendita del 2018 come esempio, con il 10% che rappresenta la media. Mentre il tuo modello tipico si concentrerebbe solo sulla cifra del 10% o avrebbe scenari "rialzo" e "orso" con una crescita rispettivamente del 15% e del 5%, questo ora fornisce informazioni sull'intera gamma di potenziali risultati attesi.

Uno dei vantaggi delle simulazioni Monte Carlo è che i risultati della coda a bassa probabilità possono innescare riflessioni e discussioni. Solo la visualizzazione di scenari al rialzo e al ribasso può introdurre il rischio che i decisori li interpretino come limiti esterni, respingendo qualsiasi scenario che si trova all'esterno. Ciò può comportare un processo decisionale imperfetto, con esposizione a risultati che esulano dalla tolleranza al rischio dell'organizzazione o dell'individuo. Anche una probabilità del 5% o dell'1% potrebbe essere inaccettabile se lo scenario in questione avrebbe conseguenze catastrofiche.

Passaggio 3. Espansione della previsione delle entrate da un anno a diversi

Con la modellazione Monte Carlo, tieni presente come le distribuzioni di incertezza e probabilità si accumulano l'una sull'altra, ad esempio nel tempo. Esaminiamo un esempio. Poiché le vendite di ogni anno dipendono dalla crescita dei precedenti, possiamo visualizzare e vedere che la nostra stima delle vendite del 2022 è più incerta di quella per il 2018 (mostrata utilizzando le deviazioni standard e gli intervalli di confidenza al 95% in ogni anno). Per semplicità, l'esempio seguente specifica la crescita per un anno, il 2018, e quindi applica lo stesso tasso di crescita a ciascuno degli anni successivi fino al 2022. Un altro approccio consiste nell'avere cinque distribuzioni indipendenti, una per ogni anno.

Passaggio 4. Continuazione del conto economico: espressione dei margini come distribuzioni di probabilità

Ora stimiamo una distribuzione di probabilità per il margine EBIT nel 2018 (evidenziato di seguito) in modo simile a come lo abbiamo fatto per la crescita delle vendite.

In questo caso, possiamo utilizzare la funzione di correlazione per simulare una situazione in cui esiste una chiara correlazione tra quota di mercato relativa e redditività, riflettendo economie di scala. Gli scenari con una maggiore crescita delle vendite rispetto al mercato e una quota di mercato relativa più elevata possono essere modellati per avere una correlazione positiva con margini EBIT più elevati. Nei settori in cui la fortuna di un'impresa è fortemente correlata con qualche altro fattore esterno, come i prezzi del petrolio oi tassi di cambio, può avere senso definire una distribuzione per quel fattore e modellare una correlazione con le vendite e la redditività.

A seconda del tempo disponibile, dell'entità della transazione e di altri fattori, spesso ha senso costruire un modello operativo e inserire in modo esplicito le variabili più incerte. Questi includono: volumi e prezzi dei prodotti, prezzi delle materie prime, tassi di cambio, principali voci di linea generali, utenti attivi mensili e entrate medie per unità (ARPU). È anche possibile modellare oltre le variabili di importo come il tempo di sviluppo, il tempo di commercializzazione o il tasso di adozione del mercato.

Passaggio 5. Stato patrimoniale e rendiconto finanziario

Utilizzando l'approccio delineato, possiamo ora continuare con lo stato patrimoniale e il rendiconto finanziario, compilando ipotesi e utilizzando distribuzioni di probabilità dove ha senso.

Una nota sugli investimenti: questo può essere modellato sia in importi assoluti che in percentuale delle vendite, potenzialmente in combinazione con investimenti graduali più grandi; un impianto di produzione può ad esempio avere un limite di capacità chiaro e un ingente investimento di espansione o una nuova struttura necessaria quando le vendite superano la soglia. Poiché ciascuna delle 1.000 o 10.000 iterazioni, ad esempio, rappresenterà un ricalcolo completo del modello, è possibile utilizzare una semplice formula che attiva il costo di investimento se/quando viene raggiunto un determinato volume.

Passaggio 6. Finalizzazione del modello

La costruzione di un modello Monte Carlo ha un passaggio aggiuntivo rispetto a un modello finanziario standard: le celle in cui vogliamo valutare i risultati devono essere specificatamente designate come celle di output. Il software salverà i risultati di ogni iterazione della simulazione affinché quelle celle possano valutarli al termine della simulazione. Tutte le celle dell'intero modello vengono ricalcolate ad ogni iterazione, ma i risultati delle iterazioni in altre celle, che non sono designate come celle di input o output, vengono perse e non possono essere analizzate al termine della simulazione. Come puoi vedere nello screenshot qui sotto, designiamo la cella del risultato MIRR come cella di output.

Una volta terminata la costruzione del modello, è il momento di eseguire la simulazione per la prima volta premendo semplicemente “avvia simulazione” e attendendo qualche secondo.

Passaggio 7. Interpretazione dei risultati

Output espressi come probabilità. Mentre il nostro modello in precedenza ci forniva un unico valore per l'IRR modificato, ora possiamo vedere chiaramente che ci sono una serie di potenziali risultati attorno a quel valore, con probabilità diverse. Questo ci consente di riformulare domande, come "Riusciremo a raggiungere il nostro tasso di ritorno all'ostacolo con questo investimento?" a "Quanto è probabile che raggiungiamo o superiamo il nostro hurdle rate?" È possibile esplorare quali risultati sono più probabili utilizzando, ad esempio, un intervallo di confidenza. La visualizzazione è utile quando si comunicano i risultati a diverse parti interessate ed è possibile sovrapporre gli output di altre transazioni per confrontare visivamente quanto sia attraente e (non) certo quella attuale rispetto ad altre (vedi sotto).

Comprendere il grado di incertezza nel risultato finale. Se generiamo un grafico della variabilità del flusso di cassa nel tempo, simile a quello che abbiamo fatto inizialmente per le vendite, diventa chiaro che la variabilità del flusso di cassa libero diventa significativa anche con un'incertezza relativamente modesta nelle vendite e negli altri input che abbiamo modellato come distribuzioni di probabilità , con risultati che vanno da circa 0,5 milioni di euro a 5,0 milioni di euro, un fattore 10x, anche con una sola deviazione standard dalla media. Questo è il risultato dell'accatastamento di presupposti incerti l'uno sull'altro, un effetto che si somma sia "verticalmente" nel corso degli anni, sia "orizzontalmente" verso il basso nel bilancio. Le visualizzazioni forniscono informazioni su entrambi i tipi di incertezza.

Analisi di sensibilità: Introduzione al grafico del tornado. Un'altra area importante è capire quali input hanno il maggiore impatto sul risultato finale. Un classico esempio è il modo in cui l'importanza del tasso di sconto o delle ipotesi di valore terminale è spesso data troppo poco peso rispetto alla previsione dei flussi di cassa. Un modo comune per gestirlo è utilizzare matrici in cui si inserisce un input chiave su ciascun asse e quindi si calcola il risultato in ciascuna cella (vedi sotto). Ciò è utile soprattutto in situazioni in cui le decisioni dipendono da uno o pochi presupposti chiave: in queste situazioni "in cosa devi credere", i decisori (ad esempio) di un comitato di investimento o di un team dirigenziale possono avere opinioni diverse su questi presupposti chiave e una matrice come quella sopra consente a ciascuno di loro di trovare un valore di risultato corrispondente al proprio punto di vista e di poter decidere, votare o dare consigli sulla base di quello.

Miglioramento con simulazioni Monte Carlo. Quando si utilizzano simulazioni Monte Carlo, questo approccio può essere integrato con un altro: il diagramma del tornado. Questa visualizzazione elenca i diversi input e ipotesi incerti sull'asse verticale e quindi mostra quanto è grande l'impatto di ciascuno sul risultato finale.

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein