Caixa de ferramentas do Forecaster: como realizar simulações de Monte Carlo
Publicados: 2022-03-11Sumário executivo
O que é uma simulação de Monte Carlo?
- As simulações de Monte Carlo modelam a probabilidade de diferentes resultados em previsões e estimativas. Eles ganham o nome da área de Monte Carlo, em Mônaco, famosa por seus cassinos sofisticados. Os resultados aleatórios são fundamentais para a técnica, assim como para a roleta e as máquinas caça-níqueis. As simulações de Monte Carlo são úteis em uma ampla variedade de campos, incluindo engenharia, gerenciamento de projetos, exploração de petróleo e gás e outras indústrias de capital intensivo, P&D e seguros. Este artigo se concentra em aplicações em finanças e negócios.
- Distribuições de probabilidade. Na simulação, as entradas incertas são descritas usando distribuições de probabilidade. Quando uma ou mais entradas são descritas como distribuições de probabilidade, a saída também se torna uma distribuição de probabilidade. Um computador extrai aleatoriamente um número de cada distribuição de entrada e calcula e salva o resultado. Isso é repetido centenas ou milhares de vezes, cada uma chamada de iteração. Quando tomadas em conjunto, essas iterações aproximam a distribuição de probabilidade do resultado final.
Tutorial Simulação Monte Carlo
- Passo 1: Escolhendo ou Construindo o Modelo. Use um modelo simples, focado em destacar os principais recursos do uso de distribuições de probabilidade. Observe que, para começar, esse modelo não é diferente de qualquer outro modelo do Excel - os plug-ins funcionam com seus modelos e planilhas existentes.
- Etapa 2: Criando a primeira distribuição de probabilidade. Primeiro, precisamos coletar as informações necessárias para fazer nossas suposições, depois precisamos escolher as distribuições de probabilidade corretas a serem inseridas. É importante observar que a fonte das principais entradas/suposições são as mesmas, independentemente de qual abordagem você adota para lidar com a incerteza. Em seguida, você percorre e substitui nossos principais valores de entrada por distribuições de probabilidade uma a uma. Em seguida, você escolherá a distribuição que deseja usar (por exemplo, normal).
- Etapa 3: expandir a previsão de receita de um ano para vários. Com a modelagem de Monte Carlo, esteja ciente de como as distribuições de incerteza e probabilidade se acumulam, como ao longo do tempo. Outra abordagem é ter cinco distribuições independentes, uma para cada ano.
- Passo 4: Expressando Margens como Distribuições de Probabilidade. Aqui podemos usar a funcionalidade de correlação para simular uma situação em que há uma correlação clara entre participação de mercado relativa e lucratividade, refletindo economias de escala. E dependendo do tempo disponível, tamanho da transação e outros fatores, geralmente faz sentido construir um modelo operacional e inserir as variáveis mais incertas explicitamente. Estes incluem: volumes e preços de produtos, preços de commodities, taxas de câmbio, principais itens de linha de despesas gerais, usuários ativos mensais e receita média por unidade (ARPU). Também é possível modelar não apenas variáveis de quantidade, como tempo de desenvolvimento, tempo de colocação no mercado ou taxa de adoção do mercado.
- Passo 5: Balanço Patrimonial e Demonstração do Fluxo de Caixa. Usando a abordagem descrita, podemos agora continuar com o balanço patrimonial e a demonstração do fluxo de caixa, preenchendo com suposições e usando distribuições de probabilidade onde fizer sentido.
- Passo 6: Finalizando o Modelo. A construção de um modelo de Monte Carlo tem uma etapa adicional em comparação com um modelo financeiro padrão: as células onde queremos avaliar os resultados precisam ser designadas especificamente como células de saída. O software salvará os resultados de cada iteração da simulação para essas células para avaliarmos após a conclusão da simulação - todas as células do modelo inteiro são recalculadas a cada iteração, mas os resultados das iterações em outras células, que não são designadas como células de entrada ou saída, são perdidas e não podem ser analisadas após o término da simulação. Depois de terminar de construir o modelo, é hora de executar a simulação pela primeira vez, simplesmente pressionando "Iniciar simulação" e aguardando alguns segundos.
- Passo 7: Interpretando os Resultados. Agora podemos ver claramente que existem vários resultados potenciais em torno desse valor, com diferentes probabilidades. Isso nos permite reformular perguntas, como "Vamos atingir nossa taxa de retorno com esse investimento?" para "Qual a probabilidade de atingirmos ou excedermos nossa taxa de resistência?" Você pode explorar quais resultados são mais prováveis, usando, por exemplo, um intervalo de confiança. A visualização é útil ao comunicar os resultados a diferentes partes interessadas, e você pode sobrepor as saídas de outras transações para comparar visualmente o quão atraente e (in)certo o atual é comparado a outros.
- A Toptal Finance pode ajudá-lo com todas as suas necessidades de modelagem, com nossos especialistas em Excel, consultores de modelagem financeira, especialistas em avaliação e especialistas em previsão financeira.
Introdução
Em primeiro lugar, a única certeza é que não há certeza. Em segundo lugar, toda decisão como consequência é uma questão de ponderar probabilidades. Terceiro, apesar da incerteza, devemos decidir e devemos agir. E, por último, precisamos julgar as decisões não apenas pelos resultados, mas como essas decisões foram tomadas. – Robert E. Rubin
Um dos aspectos mais importantes e desafiadores da previsão é lidar com a incerteza inerente ao exame do futuro. Tendo construído e preenchido centenas de modelos financeiros e operacionais para LBOs, captação de recursos para startups, orçamentos, M&A e planos estratégicos corporativos desde 2003, testemunhei uma ampla variedade de abordagens para fazer isso. Cada CEO, CFO, membro do conselho, investidor ou membro do comitê de investimento traz sua própria experiência e abordagem para projeções financeiras e incertezas – influenciadas por diferentes incentivos. Muitas vezes, comparar os resultados reais com as projeções fornece uma avaliação de quão grandes podem ser os desvios entre as previsões e os resultados reais e, portanto, a necessidade de entender e reconhecer explicitamente a incerteza.
Inicialmente, comecei usando análises de cenário e sensibilidade para modelar a incerteza e ainda as considero ferramentas muito úteis. Desde que adicionei as simulações de Monte Carlo à minha caixa de ferramentas em 2010, descobri que elas são uma ferramenta extremamente eficaz para refinar e melhorar a forma como você pensa sobre riscos e probabilidades. Eu usei a abordagem para tudo, desde a construção de avaliações de DCF, avaliação de opções de compra em M&A e discussão de riscos com credores para buscar financiamento e orientar a alocação de financiamento de VC para startups. A abordagem sempre foi bem recebida pelos membros do conselho, investidores e equipes da alta administração. Neste artigo, forneço um tutorial passo a passo sobre como usar simulações de Monte Carlo na prática, construindo um modelo de avaliação DCF.
Toda decisão é uma questão de ponderar probabilidades
Antes de começar com o estudo de caso, vamos rever algumas abordagens diferentes para lidar com a incerteza. O conceito de valor esperado — a média ponderada de probabilidade dos fluxos de caixa em todos os cenários possíveis — é Finanças 101. Mas os profissionais de finanças e os tomadores de decisão de forma mais ampla adotam abordagens muito diferentes ao traduzir essa simples percepção para a prática. A abordagem pode variar de simplesmente não reconhecer ou discutir a incerteza, por um lado, a modelos e softwares sofisticados, por outro. Em alguns casos, as pessoas acabam gastando mais tempo discutindo probabilidades do que calculando fluxos de caixa.
Além de simplesmente não abordá-lo, vamos examinar algumas maneiras de lidar com a incerteza em projeções de médio ou longo prazo. Muitos deles devem ser familiares para você.
Criando um cenário. Essa abordagem é o padrão para orçamentos, muitas startups e até decisões de investimento. Além de não conter nenhuma informação sobre o grau de incerteza ou reconhecimento de que os resultados podem diferir das projeções, pode ser ambíguo e ser interpretado de forma diferente de acordo com o stakeholder. Alguns podem interpretá-lo como uma meta estendida, onde o resultado real é mais provável de ficar aquém do que exceder. Alguns o veem como um desempenho básico com mais vantagens do que desvantagens. Outros podem vê-lo como um "Caso Base" com probabilidade 50/50 para cima e para baixo. Em algumas abordagens, especialmente para startups, é muito ambicioso e o fracasso ou déficit é o resultado mais provável, mas uma taxa de desconto mais alta é usada na tentativa de explicar o risco. | 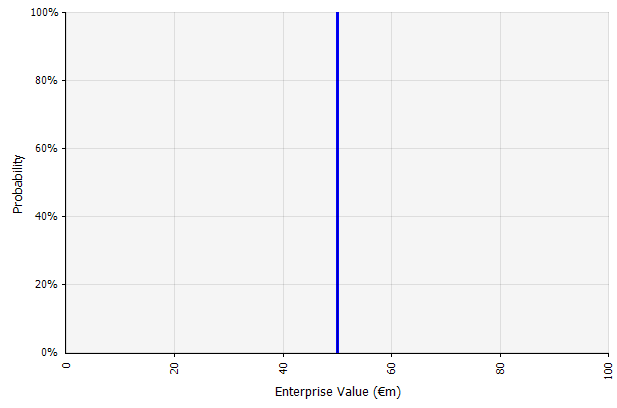 As entradas na previsão de fluxo de caixa de longo prazo sob esta abordagem são todas estimativas pontuais, produzindo um resultado de estimativa pontual de € 50 milhões neste exemplo, com uma probabilidade implícita de 100%. |
Criando vários cenários. Essa abordagem reconhece que é improvável que a realidade se desenrole de acordo com um único plano.
| 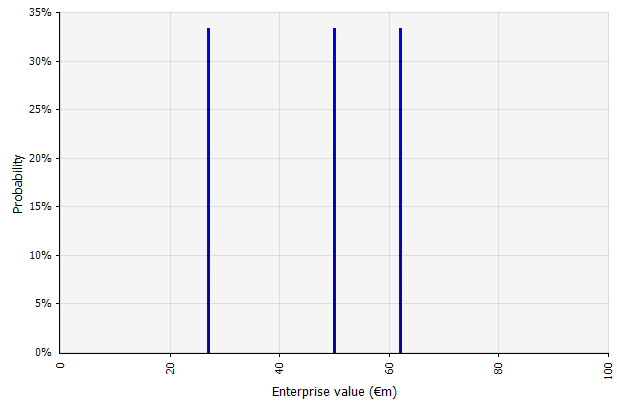 Os três cenários diferentes produzem três resultados diferentes, aqui considerados igualmente prováveis. As probabilidades de resultados fora dos cenários alto e baixo não são consideradas. |
Criando casos básicos, positivos e negativos com probabilidades explicitamente reconhecidas. Ou seja, os casos de urso e touro contêm, por exemplo, uma probabilidade de 25% em cada cauda, e a estimativa do valor justo representa o ponto médio. Um benefício útil disso de uma perspectiva de gerenciamento de risco é a análise explícita do risco de cauda, ou seja, eventos fora dos cenários de alta e baixa. | Ilustração do Manual de Avaliação da Morningstar 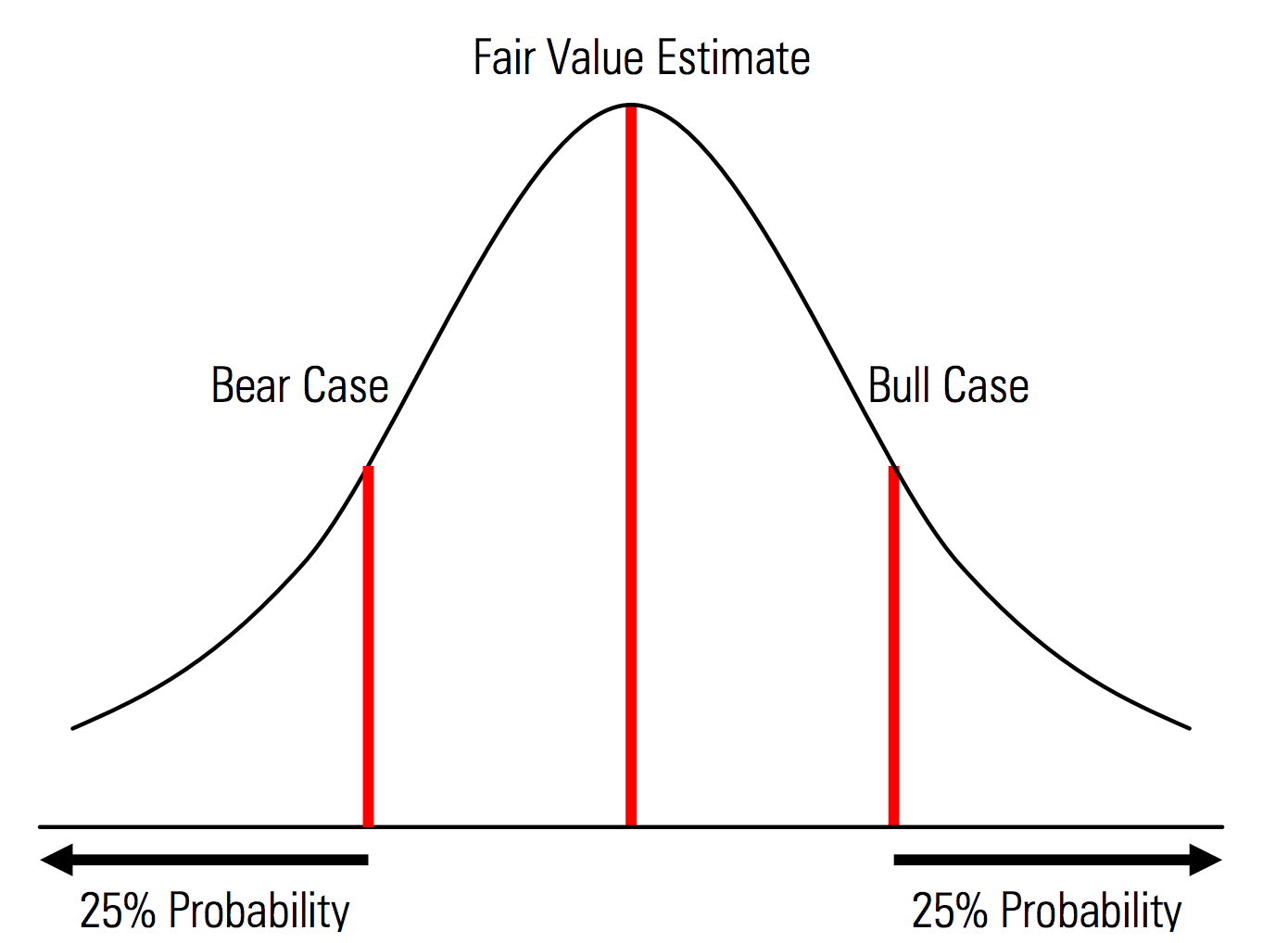 |
Usando distribuições de probabilidade e simulações de Monte Carlo. O uso de distribuições de probabilidade permite modelar e visualizar toda a gama de resultados possíveis na previsão. Isso pode ser feito não apenas em um nível agregado, mas também para entradas individuais detalhadas, suposições e direcionadores. Os métodos de Monte Carlo são então usados para calcular as distribuições de probabilidade resultantes em um nível agregado, permitindo a análise de como várias variáveis incertas contribuem para a incerteza dos resultados gerais. Talvez mais importante, a abordagem força todos os envolvidos na análise e decisão a reconhecer explicitamente a incerteza inerente à previsão e a pensar em probabilidades. Assim como as outras abordagens, isso tem suas desvantagens, incluindo o risco de falsa precisão e excesso de confiança resultante que pode vir com o uso de um modelo mais sofisticado, e o trabalho adicional necessário para selecionar distribuições de probabilidade adequadas e estimar seus parâmetros onde, de outra forma, apenas estimativas pontuais seriam usado. | 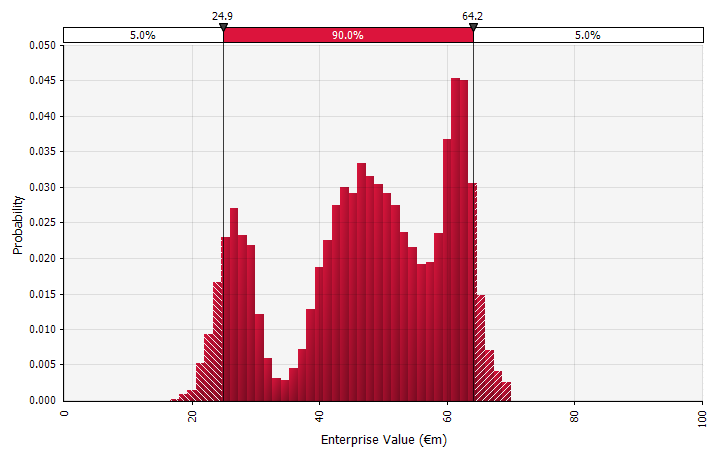 |
O que é uma simulação de Monte Carlo?
As simulações de Monte Carlo modelam a probabilidade de diferentes resultados em previsões e estimativas financeiras. Eles ganham o nome da área de Monte Carlo, em Mônaco, mundialmente famosa por seus cassinos sofisticados; resultados aleatórios são centrais para a técnica, assim como são para roleta e máquinas caça-níqueis. As simulações de Monte Carlo são úteis em uma ampla variedade de campos, incluindo engenharia, gerenciamento de projetos, exploração de petróleo e gás e outras indústrias de capital intensivo, P&D e seguros; aqui, concentro-me em aplicações em finanças e negócios.
Distribuições de probabilidade
Na simulação, as entradas incertas são descritas usando distribuições de probabilidade, descritas por parâmetros como média e desvio padrão. Exemplos de entradas em projeções financeiras podem ser desde receita e margens até algo mais granular, como preços de commodities, despesas de capital para uma expansão ou taxas de câmbio.
Quando uma ou mais entradas são descritas como distribuições de probabilidade, a saída também se torna uma distribuição de probabilidade. Um computador extrai aleatoriamente um número de cada distribuição de entrada e calcula e salva o resultado. Isso é repetido centenas, milhares ou dezenas de milhares de vezes, cada uma chamada de iteração. Quando tomadas em conjunto, essas iterações aproximam a distribuição de probabilidade do resultado final.
Tipos de entradas
As distribuições de entrada podem ser contínuas , onde o valor gerado aleatoriamente pode assumir qualquer valor sob a distribuição (por exemplo, uma distribuição normal), ou discretas , onde as probabilidades são anexadas a dois ou mais cenários distintos.
Uma simulação também pode conter uma mistura de distribuições de diferentes tipos. Tomemos, por exemplo, um projeto de P&D farmacêutico com vários estágios, cada um com uma probabilidade discreta de sucesso ou fracasso. Isso pode ser combinado com distribuições contínuas descrevendo valores de investimento incertos necessários para cada estágio e receitas potenciais se o projeto resultar em um produto que chegue ao mercado. O gráfico abaixo mostra o resultado de tal simulação: uma probabilidade de ~65% de perder todo o investimento de €5 milhões a €50 milhões (valor presente) e uma probabilidade de ~35% de um ganho líquido mais provável na faixa de € 100 a € 250 — informações que seriam perdidas se as principais métricas de saída, como MIRR ou NPV, fossem mostradas como estimativas pontuais em vez de distribuições de probabilidade.
Simulações de Monte Carlo na Prática
Uma razão pela qual as simulações de Monte Carlo não são mais amplamente utilizadas é porque as ferramentas típicas de finanças do dia-a-dia não as suportam muito bem. O Excel e o Google Sheets contêm um número ou resultado de fórmula em cada célula e, embora possam definir distribuições de probabilidade e gerar números aleatórios, construir um modelo financeiro com a funcionalidade Monte Carlo do zero é complicado. E, embora muitas instituições financeiras e empresas de investimento usem simulações de Monte Carlo para avaliar derivativos, analisar portfólios e muito mais, suas ferramentas são normalmente desenvolvidas internamente, proprietárias ou proibitivamente caras, tornando-as inacessíveis ao profissional de finanças individual.
Assim, quero chamar a atenção para os plugins do Excel, como @RISK da Palisade, ModelRisk da Vose e RiskAMP, que simplificam muito o trabalho com simulações de Monte Carlo e permitem integrá-los em seus modelos existentes. No passo a passo a seguir, usarei o @RISK.
Estudo de caso: Projeções de fluxo de caixa com simulação de Monte Carlo
Vamos rever um exemplo simples que ilustra os conceitos-chave de uma simulação de Monte Carlo: uma previsão de fluxo de caixa de cinco anos. Neste passo a passo, configuro e preencho um modelo básico de fluxo de caixa para fins de avaliação, substituo gradualmente as entradas por distribuições de probabilidade e, finalmente, executo a simulação e analiso os resultados.
Etapa 1. Escolhendo ou Construindo o Modelo
Para começar, uso um modelo simples, focado em destacar os principais recursos do uso de distribuições de probabilidade. Observe que, para começar, esse modelo não é diferente de nenhum outro modelo do Excel; os plugins que mencionei acima funcionam com seus modelos e planilhas existentes. O modelo abaixo é uma versão simples pronta para uso, preenchida com suposições para formar um cenário.
Etapa 2. Criando a primeira distribuição de probabilidade
Primeiro, precisamos coletar as informações necessárias para fazer nossas suposições, depois precisamos escolher as distribuições de probabilidade corretas a serem inseridas. É importante observar que a fonte das principais entradas/suposições são as mesmas, independentemente de qual abordagem você adota para lidar com a incerteza. A due diligence comercial, uma revisão abrangente do plano de negócios da empresa no contexto do desenvolvimento de mercado projetado, tendências do setor e dinâmica competitiva, normalmente inclui extrapolação de dados históricos, incorporação de opinião de especialistas, realização de pesquisas de mercado e entrevistas com participantes do mercado. Na minha experiência, especialistas e participantes do mercado ficam felizes em discutir diferentes cenários, riscos e gamas de resultados. No entanto, a maioria não descreve explicitamente distribuições de probabilidade.
Vamos agora percorrer e substituir nossos principais valores de entrada por distribuições de probabilidade uma a uma, começando com o crescimento de vendas estimado para o primeiro ano de previsão (2018). O plugin @RISK para Excel pode ser avaliado com uma avaliação gratuita de 15 dias para que você possa baixá-lo do site da Palisade e instalá-lo com apenas alguns cliques. Com o plugin @RISK habilitado, selecione a célula na qual deseja a distribuição e selecione “Definir distribuição” no menu.
Você então seleciona uma da paleta de distribuições que aparece. O software @RISK oferece mais de 70 distribuições diferentes para escolher, então escolher uma pode parecer difícil no começo. Abaixo está um guia para um punhado que eu uso com mais frequência:
Normal. Definido por média e desvio padrão. Este é um bom ponto de partida devido à sua simplicidade e adequado como uma extensão da abordagem Morningstar, onde você define uma distribuição que cobre cenários ou intervalos talvez já definidos para uma determinada entrada, garantindo que os casos sejam simétricos em torno do caso base e que as probabilidades em cada cauda parecem razoáveis (digamos 25% como no exemplo Morningstar). | 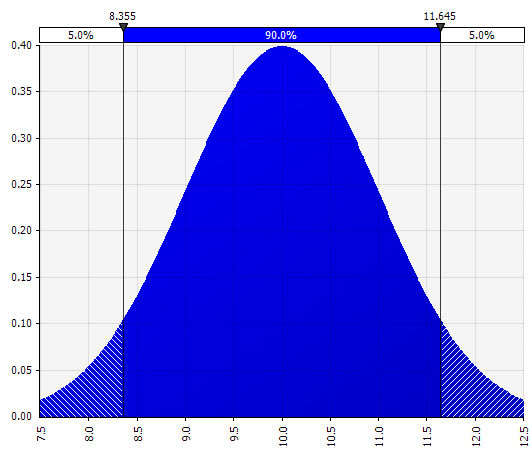 |
Momentos Johnson. Escolher isso permite que você defina distribuições distorcidas e distribuições com caudas mais grossas ou mais finas (adicionando tecnicamente parâmetros de assimetria e curtose). Nos bastidores, isso usa um algoritmo para escolher uma das quatro distribuições que reflete os quatro parâmetros escolhidos, mas que é invisível para o usuário --- tudo o que temos que focar são os parâmetros. 
| 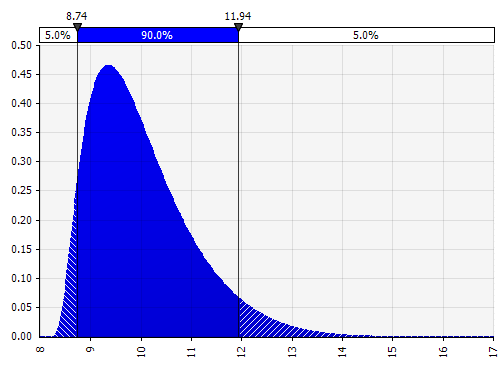 |
Discreto. Onde as probabilidades são dadas para dois ou mais valores específicos. Voltando ao exemplo do projeto de P&D em estágios no início, a probabilidade de sucesso em cada estágio é modelada como uma distribuição discreta binária, com um resultado de 1 representando sucesso e 0 fracasso. | 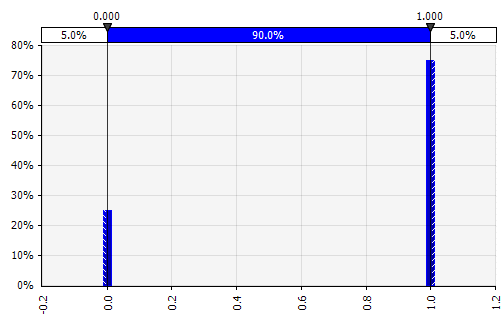 |
Encaixe de Distribuição. Quando você tem uma grande quantidade de pontos de dados históricos, a funcionalidade de ajuste de distribuição é útil. Isso não significa três ou quatro anos de crescimento histórico de vendas, por exemplo, mas dados de séries temporais, como preços de commodities, taxas de câmbio ou outros preços de mercado, onde o histórico pode fornecer informações úteis sobre tendências futuras e o grau de incerteza. | 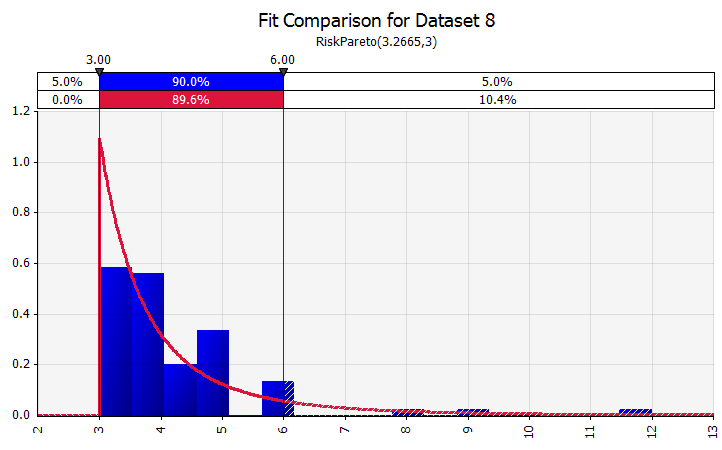 |
Combinando várias distribuições diferentes em uma. Para mitigar o impacto potencial de vieses individuais, muitas vezes é uma boa ideia incorporar a entrada de diferentes fontes em uma suposição e/ou revisar e discutir os resultados. Existem diferentes abordagens:
| 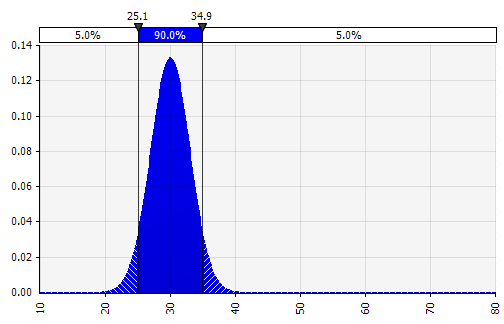 Peso: 20% 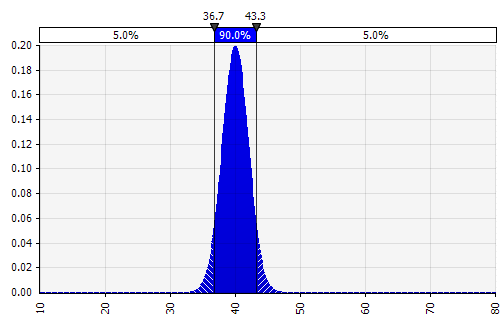 Peso: 20% 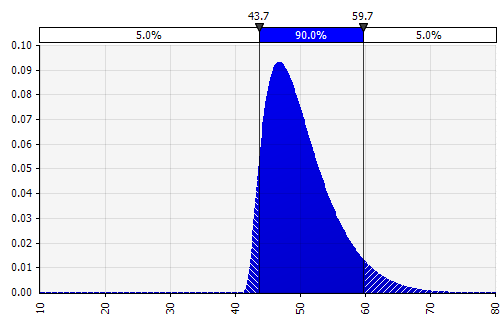 Peso: 60% 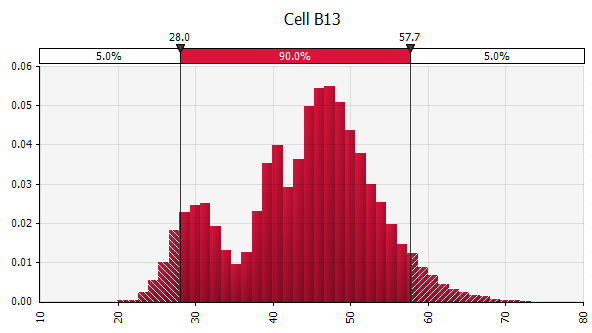 |
Mão livre. Para ilustrar rapidamente uma distribuição como parte de discussões ou se você precisar de uma distribuição ao rascunhar um modelo que não é facilmente criado a partir da paleta existente, a funcionalidade à mão livre é útil. Como o nome indica, isso permite que você desenhe a distribuição usando uma ferramenta de pintura simples. | 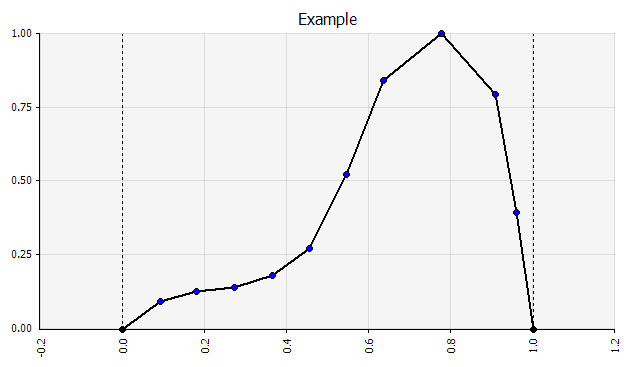 |
Agora vemos uma visualização da distribuição, com alguns parâmetros do lado esquerdo. Os símbolos de média e desvio padrão devem parecer familiares. No caso de uma distribuição normal, a média seria o que inserimos anteriormente como um único valor na célula. Aqui está a distribuição de probabilidade de vendas de 2018 como exemplo, com 10% representando a média. Considerando que seu modelo típico se concentraria apenas no valor de 10%, ou teria cenários de “touro” e “urso” com talvez 15% e 5% de crescimento, respectivamente, isso agora fornece informações sobre toda a gama de resultados potenciais esperados.
Um benefício das simulações de Monte Carlo é que os resultados finais de baixa probabilidade podem desencadear reflexões e discussões. Apenas a exibição de cenários positivos e negativos pode apresentar o risco de que os tomadores de decisão os interpretem como os limites externos, descartando quaisquer cenários que estejam fora. Isso pode resultar em uma tomada de decisão falha, com exposição a resultados que estão além da tolerância ao risco da organização ou do indivíduo. Mesmo uma probabilidade de 5% ou 1% pode ser inaceitável se o cenário em questão tiver consequências catastróficas.
Etapa 3. Expandindo a previsão de receita de um ano para vários
Com a modelagem de Monte Carlo, esteja ciente de como as distribuições de incerteza e probabilidade se acumulam, como ao longo do tempo. Vamos rever um exemplo. Como as vendas de cada ano dependem do crescimento dos anteriores, podemos visualizar e ver que nossa estimativa de vendas de 2022 é mais incerta do que a de 2018 (mostrada usando os desvios padrão e intervalos de confiança de 95% em cada ano). Para simplificar, o exemplo abaixo especifica o crescimento para um ano, 2018, e aplica a mesma taxa de crescimento para cada um dos anos seguintes até 2022. Outra abordagem é ter cinco distribuições independentes, uma para cada ano.
Etapa 4. Continuando a Demonstração de Resultados - Expressando Margens como Distribuições de Probabilidade
Agora estimamos uma distribuição de probabilidade para a margem EBIT em 2018 (destacada abaixo) da mesma forma que fizemos para o crescimento das vendas.
Aqui, podemos usar a função de correlação para simular uma situação em que há uma correlação clara entre a participação relativa de mercado e a lucratividade, refletindo economias de escala. Cenários com crescimento de vendas mais alto em relação ao mercado e participação de mercado correspondentemente mais alta podem ser modelados para ter uma correlação positiva com margens EBIT mais altas. Em indústrias em que a fortuna de uma empresa está fortemente correlacionada com algum outro fator externo, como preços do petróleo ou taxas de câmbio, definir uma distribuição para esse fator e modelar uma correlação com vendas e lucratividade pode fazer sentido.
Dependendo do tempo disponível, tamanho da transação e outros fatores, geralmente faz sentido construir um modelo operacional e inserir as variáveis mais incertas explicitamente. Estes incluem: volumes e preços de produtos, preços de commodities, taxas de câmbio, principais itens de linha de despesas gerais, usuários ativos mensais e receita média por unidade (ARPU). Também é possível modelar além de variáveis de quantidade, como tempo de desenvolvimento, tempo de lançamento no mercado ou taxa de adoção do mercado.
Etapa 5. Balanço Patrimonial e Demonstração do Fluxo de Caixa
Usando a abordagem descrita, podemos agora continuar com o balanço patrimonial e a demonstração do fluxo de caixa, preenchendo com suposições e usando distribuições de probabilidade onde fizer sentido.
Uma observação sobre capex: isso pode ser modelado em valores absolutos ou como uma porcentagem das vendas, potencialmente em combinação com investimentos graduais maiores; uma instalação de fabricação pode, por exemplo, ter um limite de capacidade claro e um grande investimento em expansão ou uma nova instalação necessária quando as vendas excederem o limite. Como cada uma das 1.000 ou 10.000 iterações será um recálculo completo do modelo, uma fórmula simples que aciona o custo do investimento se/quando um determinado volume for atingido pode ser usada.
Etapa 6. Finalizando o Modelo
A construção de um modelo de Monte Carlo tem uma etapa adicional em comparação com um modelo financeiro padrão: as células onde queremos avaliar os resultados precisam ser designadas especificamente como células de saída. O software salvará os resultados de cada iteração da simulação para essas células para que possamos avaliar após a conclusão da simulação. Todas as células do modelo inteiro são recalculadas a cada iteração, mas os resultados das iterações em outras células, que não são designadas como células de entrada ou saída, são perdidos e não podem ser analisados após o término da simulação. Como você pode ver na captura de tela abaixo, designamos a célula de resultado MIRR como uma célula de saída.
Depois de terminar de construir o modelo, é hora de executar a simulação pela primeira vez simplesmente pressionando “iniciar simulação” e aguardando alguns segundos.
Etapa 7. Interpretando os Resultados
Saídas expressas como probabilidades. Enquanto nosso modelo anteriormente nos dava um único valor para a TIR modificada, agora podemos ver claramente que existem vários resultados potenciais em torno desse valor, com diferentes probabilidades. Isso nos permite reformular perguntas, como “Vamos atingir nossa taxa de retorno com esse investimento?” para "Qual a probabilidade de atingirmos ou excedermos nossa taxa de resistência?" Você pode explorar quais resultados são mais prováveis usando, por exemplo, um intervalo de confiança. A visualização é útil ao comunicar os resultados a diferentes partes interessadas, e você pode sobrepor as saídas de outras transações para comparar visualmente o quão atraente e (in)certa a atual é comparada a outras (veja abaixo).
Compreender o grau de incerteza no resultado final. Se gerarmos um gráfico de variabilidade do fluxo de caixa ao longo do tempo, semelhante ao que fizemos inicialmente para as vendas, fica claro que a variabilidade do fluxo de caixa livre se torna significativa mesmo com incerteza relativamente modesta nas vendas e nas outras entradas que modelamos como distribuições de probabilidade , com resultados variando de cerca de € 0,5 milhão a € 5,0 milhões - um fator de 10x - mesmo apenas um desvio padrão da média. Este é o resultado de empilhar suposições incertas umas sobre as outras, um efeito que se compõe tanto “verticalmente” ao longo dos anos quanto “horizontalmente” nas demonstrações financeiras. As visualizações fornecem informações sobre os dois tipos de incerteza.
Análise de sensibilidade: Apresentando o gráfico de tornado. Outra área importante é entender quais insumos têm maior impacto no seu resultado final. Um exemplo clássico é como a importância da taxa de desconto ou das premissas de valor terminal geralmente recebe pouco peso em relação à previsão de fluxo de caixa. Uma maneira comum de lidar com isso é usando matrizes onde você coloca uma entrada de chave em cada eixo e calcula o resultado em cada célula (veja abaixo). Isso é útil especialmente em situações em que as decisões dependem de uma ou algumas premissas-chave – nessas situações “no que você tem que acreditar”, os tomadores de decisão em (por exemplo) um comitê de investimento ou uma equipe de gerenciamento sênior podem ter visões diferentes de essas suposições-chave, e uma matriz como a acima permite que cada um deles encontre um valor de resultado correspondente à sua visão e possa decidir, votar ou dar conselhos com base nisso.
Aprimoramento com simulações de Monte Carlo. Ao usar simulações de Monte Carlo, essa abordagem pode ser complementada com outra: o diagrama de tornado. Esta visualização lista as diferentes entradas e suposições incertas no eixo vertical e, em seguida, mostra o tamanho do impacto de cada um no resultado final.
This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.
Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.
A Few Words of Caution: Different Types of Uncertainty
Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb
It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.
In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.
The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.
In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.
At the End of the Day, It's about the Mindset, Not the Technical Solution
There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.
I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.
Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.
I spend 98% of my time on 2% probabilities – Lloyd Blankfein
