Kotak Alat Peramal: Cara Melakukan Simulasi Monte Carlo

Ringkasan bisnis plan

pengantar

Pertama, satu-satunya kepastian adalah tidak ada kepastian. Kedua, setiap keputusan sebagai konsekuensinya adalah masalah menimbang probabilitas. Ketiga, terlepas dari ketidakpastian kita harus memutuskan dan kita harus bertindak. Dan terakhir kita perlu menilai keputusan tidak hanya berdasarkan hasil, tetapi bagaimana keputusan itu dibuat. – Robert E. Rubin

Salah satu aspek peramalan yang paling penting dan menantang adalah menangani ketidakpastian yang melekat dalam memeriksa masa depan. Setelah membangun dan mengisi ratusan model keuangan dan operasi untuk LBO, penggalangan dana awal, anggaran, M&A, dan rencana strategis perusahaan sejak tahun 2003, saya telah menyaksikan berbagai pendekatan untuk melakukannya. Setiap CEO, CFO, anggota dewan, investor, atau anggota komite investasi membawa pengalaman dan pendekatan mereka sendiri terhadap proyeksi keuangan dan ketidakpastian—dipengaruhi oleh insentif yang berbeda. Seringkali, membandingkan hasil aktual dengan proyeksi memberikan apresiasi terhadap seberapa besar penyimpangan antara perkiraan dan hasil aktual, dan oleh karena itu perlunya memahami dan secara eksplisit mengenali ketidakpastian.

Saya awalnya mulai menggunakan analisis skenario dan sensitivitas untuk memodelkan ketidakpastian, dan masih menganggapnya sebagai alat yang sangat berguna. Sejak menambahkan simulasi Monte Carlo ke kotak peralatan saya pada tahun 2010, saya telah menemukan mereka sebagai alat yang sangat efektif untuk menyempurnakan dan meningkatkan cara Anda berpikir tentang risiko dan probabilitas. Saya telah menggunakan pendekatan untuk segala hal mulai dari menyusun valuasi DCF, menilai opsi panggilan dalam M&A, dan mendiskusikan risiko dengan pemberi pinjaman hingga mencari pembiayaan dan memandu alokasi pendanaan VC untuk perusahaan rintisan. Pendekatan ini selalu diterima dengan baik oleh anggota dewan, investor, dan tim manajemen senior. Pada artikel ini, saya memberikan tutorial langkah demi langkah tentang penggunaan simulasi Monte Carlo dalam praktik dengan membangun model penilaian DCF.

Setiap Keputusan Adalah Masalah Menimbang Probabilitas

Sebelum memulai studi kasus, mari kita tinjau beberapa pendekatan berbeda untuk menangani ketidakpastian. Konsep nilai yang diharapkan —rata-rata tertimbang probabilitas arus kas dalam semua skenario yang mungkin—adalah Keuangan 101. Tetapi profesional keuangan, dan pengambil keputusan secara lebih luas, mengambil pendekatan yang sangat berbeda ketika menerjemahkan wawasan sederhana ini ke dalam praktik. Pendekatannya dapat berkisar dari sekadar tidak mengenali atau mendiskusikan ketidakpastian sama sekali, di satu sisi, hingga model dan perangkat lunak yang canggih di sisi lain. Dalam beberapa kasus, orang akhirnya menghabiskan lebih banyak waktu untuk mendiskusikan probabilitas daripada menghitung arus kas.

Selain tidak membahasnya, mari kita periksa beberapa cara menangani ketidakpastian dalam proyeksi jangka menengah atau panjang. Banyak dari ini harus akrab bagi Anda.

Membuat satu skenario. Pendekatan ini adalah default untuk anggaran, banyak startup, dan bahkan keputusan investasi. Selain tidak mengandung informasi apapun tentang tingkat ketidakpastian atau pengakuan bahwa hasil mungkin berbeda dari proyeksi, dapat menjadi ambigu dan ditafsirkan berbeda menurut pemangku kepentingan. Beberapa mungkin menafsirkannya sebagai target peregangan, di mana hasil aktual lebih mungkin gagal daripada melebihi. Beberapa melihatnya sebagai kinerja dasar dengan lebih banyak sisi positif daripada sisi negatifnya. Orang lain mungkin melihatnya sebagai "Kasus Dasar" dengan probabilitas 50/50 naik turun. Dalam beberapa pendekatan, terutama untuk pemula, ini sangat ambisius dan kegagalan atau kekurangan adalah hasil yang lebih mungkin sejauh ini, tetapi tingkat diskonto yang lebih tinggi digunakan dalam upaya untuk memperhitungkan risiko.	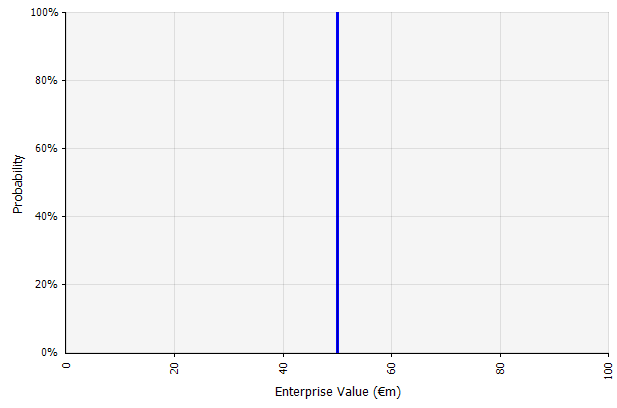Masukan dalam perkiraan arus kas jangka panjang di bawah pendekatan ini adalah semua perkiraan titik, menghasilkan hasil perkiraan titik €50 juta dalam contoh ini, dengan probabilitas implisit 100%.
Membuat beberapa skenario. Pendekatan ini mengakui bahwa realitas tidak mungkin terungkap menurut satu rencana yang diberikan. 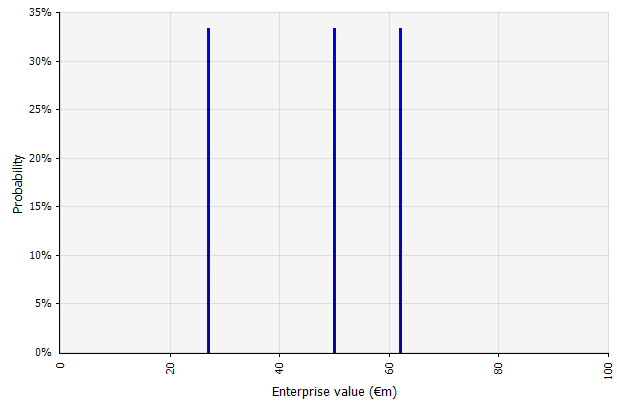Dalam bentuknya yang paling sederhana, analisis sensitivitas, ini dapat mensimulasikan dampak, misalnya, pertumbuhan penjualan 10% di atas dan di bawah kasus dasar, dengan menggunakan campuran biaya tetap, semi-variabel, dan variabel tertentu untuk memperkirakan laba. dampak. Dalam bentuk yang lebih kompleks, Anda memikirkan masa depan dari perspektif yang sama sekali berbeda untuk setiap skenario, dan menganalisis dampak perkembangan teknologi, dinamika persaingan, dan tren makro yang berbeda terhadap kinerja perusahaan. Seringkali, sayangnya, skenario dipilih secara sewenang-wenang, dan terkadang dengan hasil akhir yang diinginkan.	Tiga skenario yang berbeda menghasilkan tiga hasil yang berbeda, di sini diasumsikan sama kemungkinannya. Probabilitas hasil di luar skenario tinggi dan rendah tidak dipertimbangkan.
Membuat kasus dasar, naik, dan turun dengan probabilitas yang dikenali secara eksplisit. Artinya, kasus beruang dan banteng mengandung, misalnya, probabilitas 25% di setiap ekor, dan estimasi nilai wajar mewakili titik tengah. Manfaat yang berguna dari ini dari perspektif manajemen risiko adalah analisis eksplisit dari tail risk, yaitu, peristiwa di luar skenario naik dan turun.	Ilustrasi dari Buku Pegangan Penilaian Morningstar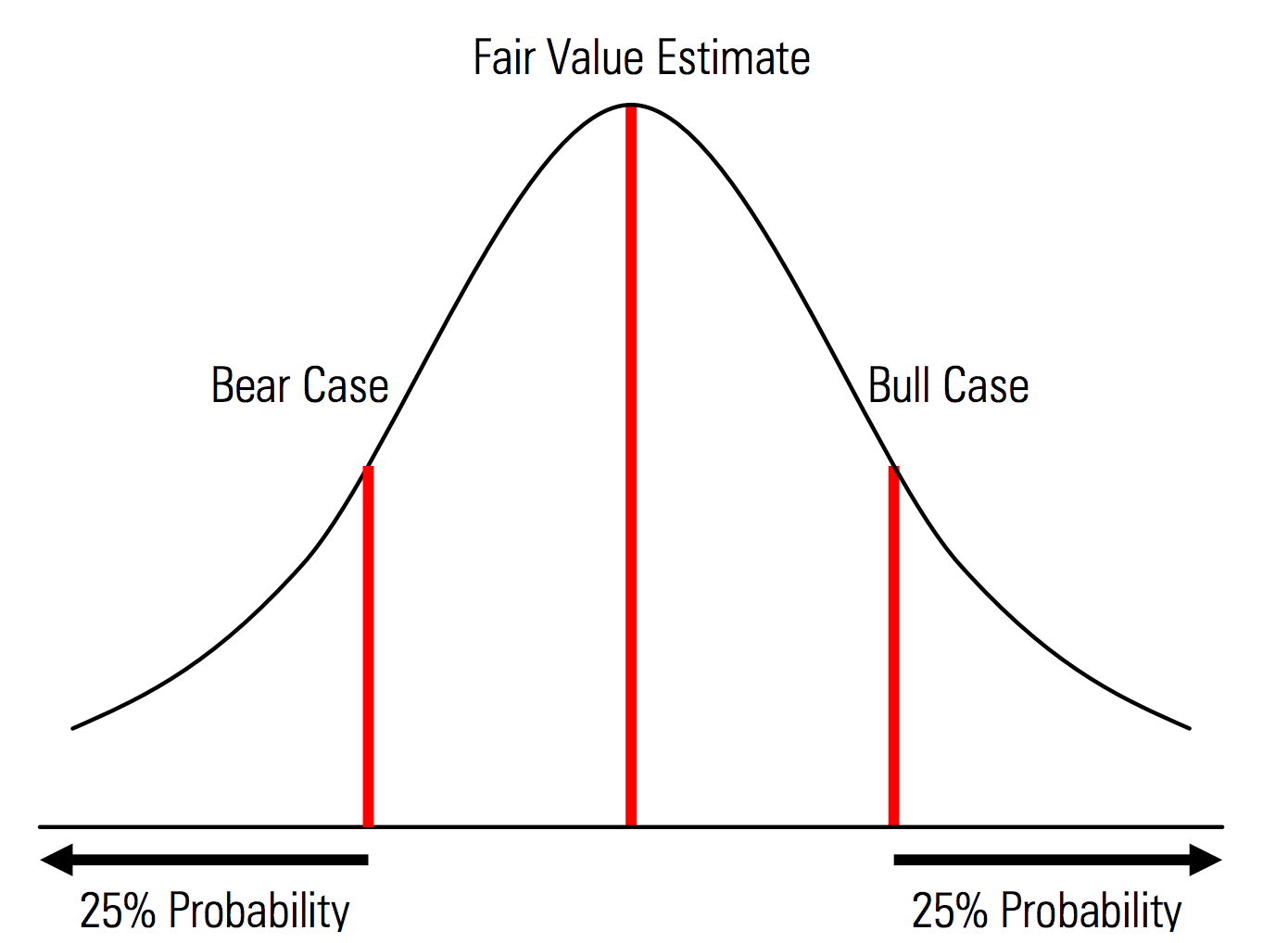
Menggunakan distribusi probabilitas dan simulasi Monte Carlo. Menggunakan distribusi probabilitas memungkinkan Anda untuk memodelkan dan memvisualisasikan berbagai kemungkinan hasil dalam perkiraan. Hal ini dapat dilakukan tidak hanya pada tingkat agregat, tetapi juga untuk masukan, asumsi, dan pendorong individual yang terperinci. Metode Monte Carlo kemudian digunakan untuk menghitung distribusi probabilitas yang dihasilkan pada tingkat agregat, memungkinkan untuk analisis tentang bagaimana beberapa variabel yang tidak pasti berkontribusi pada ketidakpastian hasil keseluruhan. Mungkin yang paling penting, pendekatan ini memaksa semua orang yang terlibat dalam analisis dan keputusan untuk secara eksplisit mengenali ketidakpastian yang melekat dalam peramalan, dan berpikir dalam probabilitas. Sama seperti pendekatan lain, ini memiliki kekurangannya, termasuk risiko presisi yang salah dan menghasilkan terlalu percaya diri yang mungkin datang dengan menggunakan model yang lebih canggih, dan pekerjaan tambahan yang diperlukan untuk memilih distribusi probabilitas yang sesuai dan memperkirakan parameternya di mana jika tidak, hanya perkiraan titik yang akan digunakan. digunakan.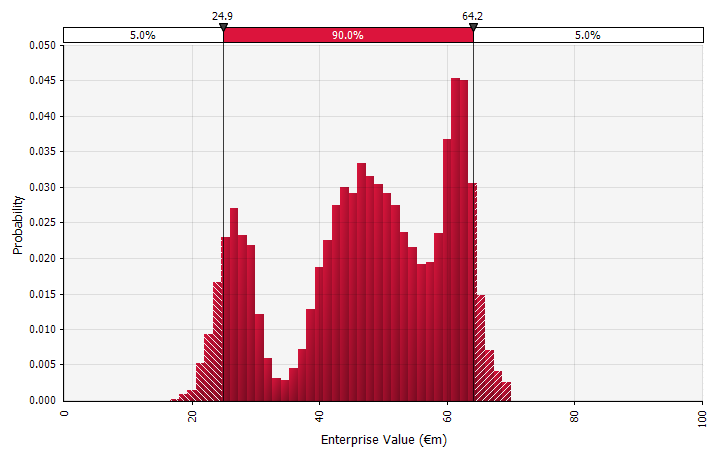

Apa itu Simulasi Monte Carlo?

Simulasi Monte Carlo memodelkan kemungkinan hasil yang berbeda dalam prakiraan dan estimasi keuangan. Mereka mendapatkan nama mereka dari area Monte Carlo di Monaco, yang terkenal di dunia dengan kasino kelas atas; hasil acak adalah inti dari teknik ini, seperti halnya pada roulette dan mesin slot. Simulasi Monte Carlo berguna dalam berbagai bidang, termasuk teknik, manajemen proyek, eksplorasi minyak & gas dan industri padat modal lainnya, R&D, dan asuransi; di sini, saya fokus pada aplikasi di bidang keuangan dan bisnis.

Distribusi Probabilitas

Dalam simulasi, input yang tidak pasti dijelaskan menggunakan distribusi probabilitas, dijelaskan oleh parameter seperti mean dan standar deviasi. Contoh input dalam proyeksi keuangan dapat berupa apa saja mulai dari pendapatan dan margin hingga sesuatu yang lebih terperinci, seperti harga komoditas, belanja modal untuk ekspansi, atau nilai tukar mata uang asing.

Ketika satu atau lebih input digambarkan sebagai distribusi probabilitas, output juga menjadi distribusi probabilitas. Komputer secara acak mengambil nomor dari setiap distribusi input dan menghitung serta menyimpan hasilnya. Ini diulang ratusan, ribuan, atau puluhan ribu kali, masing-masing disebut iterasi. Ketika diambil bersama-sama, iterasi ini mendekati distribusi probabilitas dari hasil akhir.

Jenis Input

Distribusi input dapat berupa kontinu , di mana nilai yang dihasilkan secara acak dapat mengambil nilai apa pun di bawah distribusi (misalnya distribusi normal), atau diskrit , di mana probabilitas melekat pada dua atau lebih skenario yang berbeda.

Sebuah simulasi juga dapat berisi campuran distribusi dari berbagai jenis. Ambil, misalnya, proyek R&D farmasi dengan beberapa tahap yang masing-masing memiliki probabilitas keberhasilan atau kegagalan yang berbeda. Ini dapat dikombinasikan dengan distribusi berkelanjutan yang menggambarkan jumlah investasi yang tidak pasti yang dibutuhkan untuk setiap tahap dan pendapatan potensial jika proyek menghasilkan produk yang mencapai pasar. Bagan di bawah ini menunjukkan output dari simulasi semacam itu: probabilitas ~65% kehilangan seluruh investasi sebesar €5 juta hingga €50 juta (nilai sekarang), dan probabilitas ~35% dari keuntungan bersih yang paling mungkin dalam kisaran €100 hingga €250—informasi yang akan hilang jika metrik keluaran utama seperti MIRR atau NPV ditampilkan sebagai perkiraan titik daripada distribusi probabilitas.

Simulasi Monte Carlo dalam Praktek

Salah satu alasan simulasi Monte Carlo tidak lebih banyak digunakan adalah karena alat keuangan sehari-hari tidak mendukungnya dengan baik. Excel dan Google Spreadsheet menyimpan satu angka atau hasil rumus di setiap sel, dan meskipun keduanya dapat menentukan distribusi probabilitas dan menghasilkan angka acak, membangun model keuangan dengan fungsionalitas Monte Carlo dari awal tidaklah praktis. Dan, sementara banyak lembaga keuangan dan perusahaan investasi menggunakan simulasi Monte Carlo untuk menilai derivatif, menganalisis portofolio, dan banyak lagi, alat mereka biasanya dikembangkan sendiri, eksklusif, atau sangat mahal—membuatnya tidak dapat diakses oleh profesional keuangan individu.

Jadi, saya ingin menarik perhatian pada plugin Excel seperti @RISK by Palisade, ModelRisk by Vose, dan RiskAMP, yang sangat menyederhanakan bekerja dengan simulasi Monte Carlo dan memungkinkan Anda untuk mengintegrasikannya dalam model yang ada. Dalam panduan berikut, saya akan menggunakan @RISK.

Studi kasus: Proyeksi Arus Kas dengan Simulasi Monte Carlo

Mari kita tinjau contoh sederhana yang menggambarkan konsep kunci dari simulasi Monte Carlo: perkiraan arus kas lima tahun. Dalam panduan ini, saya menyiapkan dan mengisi model arus kas dasar untuk tujuan penilaian, secara bertahap mengganti input dengan distribusi probabilitas, dan akhirnya menjalankan simulasi dan menganalisis hasilnya.

Langkah 1. Memilih atau Membangun Model

Untuk memulai, saya menggunakan model sederhana, yang berfokus pada penyorotan fitur utama penggunaan distribusi probabilitas. Perhatikan bahwa, untuk memulai, model ini tidak berbeda dengan model Excel lainnya; plugin yang saya sebutkan di atas berfungsi dengan model dan spreadsheet Anda yang ada. Model di bawah ini adalah versi off-the-shelf sederhana yang diisi dengan asumsi untuk membentuk satu skenario.

Langkah 2. Membuat Distribusi Probabilitas Pertama

Pertama, kita perlu mengumpulkan informasi yang diperlukan untuk membuat asumsi kita, kemudian kita perlu memilih distribusi probabilitas yang benar untuk dimasukkan. Penting untuk dicatat bahwa sumber input/asumsi utama adalah sama terlepas dari pendekatan mana yang Anda ambil untuk menangani ketidakpastian. Uji tuntas komersial, tinjauan komprehensif rencana bisnis perusahaan dalam konteks perkembangan pasar yang diproyeksikan, tren industri, dan dinamika persaingan, biasanya mencakup ekstrapolasi dari data historis, menggabungkan pendapat ahli, melakukan riset pasar, dan mewawancarai pelaku pasar. Dalam pengalaman saya, para ahli dan pelaku pasar dengan senang hati mendiskusikan skenario, risiko, dan rentang hasil yang berbeda. Namun, sebagian besar tidak secara eksplisit menggambarkan distribusi probabilitas.

Sekarang mari kita menelusuri dan mengganti nilai input utama kita dengan distribusi probabilitas satu per satu, dimulai dengan perkiraan pertumbuhan penjualan untuk tahun perkiraan pertama (2018). Plugin @RISK untuk Excel dapat dievaluasi dengan uji coba gratis 15 hari sehingga Anda dapat mengunduhnya dari situs web Palisade dan menginstalnya dengan beberapa klik. Dengan plugin @RISK diaktifkan, pilih sel tempat Anda ingin distribusi dan pilih "Tentukan distribusi" di menu.

Anda kemudian memilih satu dari palet distribusi yang muncul. Perangkat lunak @RISK menawarkan lebih dari 70 distribusi yang berbeda untuk dipilih, jadi memilih salah satu mungkin tampak berlebihan pada awalnya. Di bawah ini adalah panduan untuk beberapa yang paling sering saya gunakan:

Normal. Didefinisikan dengan mean dan standar deviasi. Ini adalah titik awal yang baik karena kesederhanaannya, dan cocok sebagai perpanjangan dari pendekatan Morningstar, di mana Anda menentukan distribusi yang mencakup skenario atau rentang yang mungkin sudah ditentukan untuk input yang diberikan, memastikan bahwa kasusnya simetris di sekitar kasus dasar dan bahwa probabilitas di setiap ekor terlihat masuk akal (katakanlah 25% seperti pada contoh Morningstar).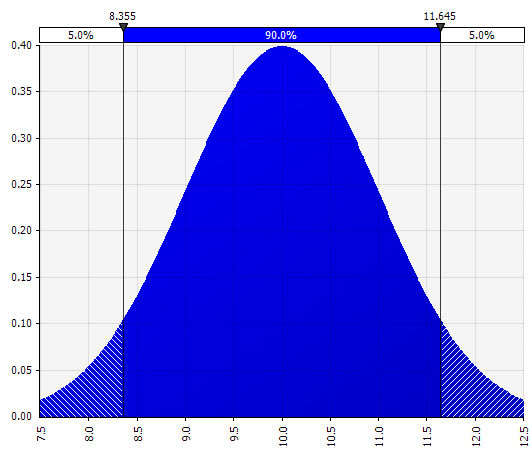
Momen Johnson. Memilih ini memungkinkan Anda untuk menentukan distribusi miring dan distribusi dengan ekor yang lebih gemuk atau lebih tipis (secara teknis menambahkan parameter kemiringan dan kurtosis). Di belakang layar, ini menggunakan algoritme untuk memilih salah satu dari empat distribusi yang mencerminkan empat parameter yang dipilih, tetapi itu tidak terlihat oleh pengguna --- yang harus kita fokuskan hanyalah parameternya. Terkadang, dalam proses pengumpulan informasi untuk input, menjadi jelas bahwa distribusi normal tidak sesuai. Misalnya, untuk perusahaan yang berada di titik terendah atau puncak siklus industri, probabilitas kinerja yang lebih baik atau lebih buruk selama lima tahun ke depan, katakanlah, tidak akan simetris. Semakin dekat ke puncak, semakin besar kemungkinan penurunan vs kinerja kuat yang berkelanjutan. Di sinilah distribusi miring dapat berguna. Banyak yang telah ditulis tentang konsep "ekor gemuk" di banyak bidang keuangan. Tampaknya distribusi normal sering tidak menggambarkan hasil aktual dengan baik, dengan kejadian yang seharusnya sangat jarang terjadi lebih sering daripada yang ditunjukkan oleh distribusi normal.
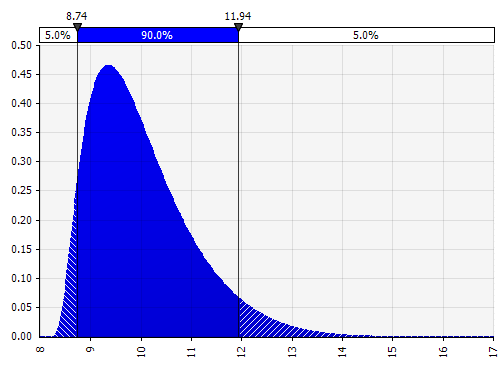Diskrit. Dimana probabilitas diberikan kepada dua atau lebih nilai spesifik. Kembali ke contoh proyek R&D bertahap di awal, probabilitas keberhasilan pada setiap tahap dimodelkan sebagai distribusi diskrit biner, dengan hasil 1 mewakili keberhasilan dan 0 kegagalan.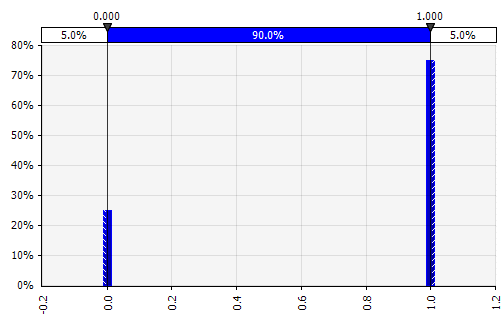
Pemasangan Distribusi. Saat Anda memiliki sejumlah besar titik data historis, fungsionalitas pemasangan distribusi berguna. Ini tidak berarti tiga atau empat tahun pertumbuhan penjualan historis, misalnya, tetapi data deret waktu seperti harga komoditas, nilai tukar mata uang, atau harga pasar lainnya di mana sejarah dapat memberikan informasi yang berguna tentang tren masa depan dan tingkat ketidakpastian.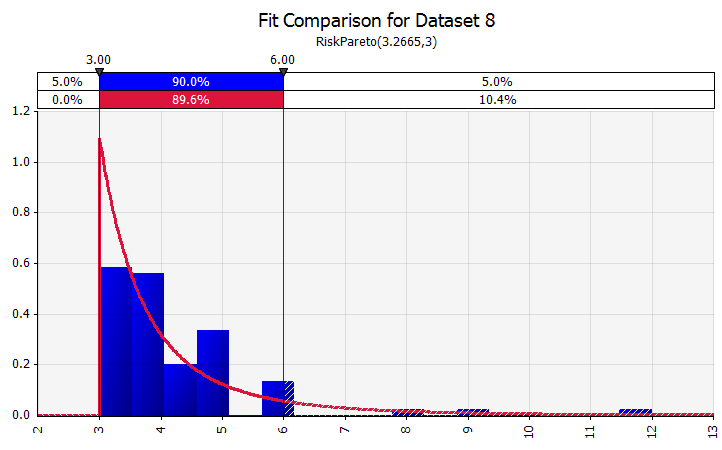
Menggabungkan beberapa distribusi yang berbeda menjadi satu. Untuk mengurangi dampak potensial dari bias individu, seringkali merupakan ide yang baik untuk memasukkan masukan dari sumber yang berbeda ke dalam asumsi, dan/atau untuk meninjau dan mendiskusikan temuan. Ada pendekatan yang berbeda: 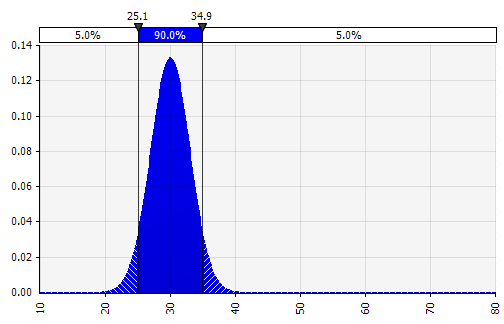Siapkan draf atau pandangan pertama dan kemudian tinjau dengan para ahli, tim manajemen yang lebih luas, atau pengambil keputusan lainnya. Kembangkan distribusi yang paling penting secara bersama-sama dalam sebuah pertemuan. Hal ini dapat mengarah pada diskusi yang baik dan hasil yang lebih baik tetapi seperti biasa komposisi kelompok sangat penting; memiliki perspektif/fungsi yang berbeda terwakili dan mendorong suasana debat yang penuh semangat namun saling menghormati tentu saja membantu. Kembangkan satu distribusi untuk setiap sumber utama, dan gabungkan semuanya, dengan bobot sesuai dengan seberapa besar keyakinan Anda pada masing-masing sumber. Jika mendapatkan masukan dari beberapa ahli yang berbeda, ada baiknya untuk membiarkan masing-masing ahli memberikan pandangannya sendiri, terlepas dari yang lain, dan kemudian digabungkan menjadi satu. Fungsi @RISK MakeRiskInput melakukan ini untuk kita.	Berat: 20% 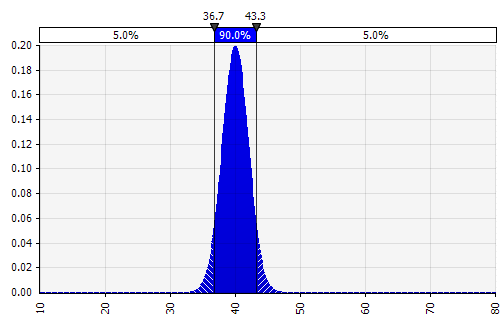+ Berat: 20% 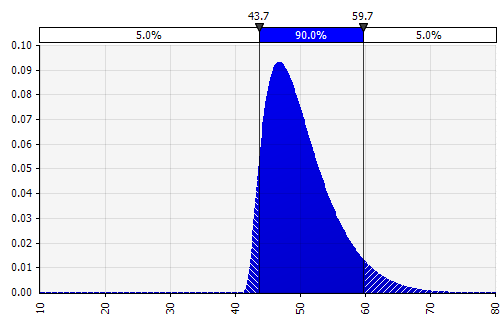+ Berat: 60% =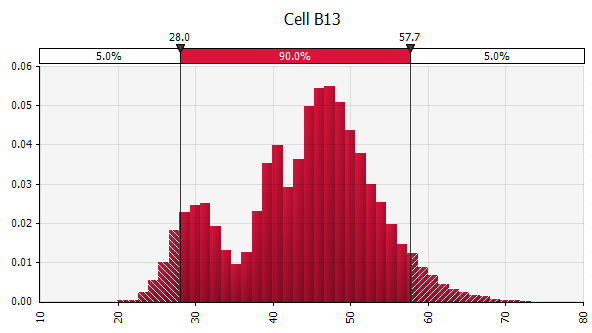
tangan bebas. Untuk mengilustrasikan distribusi dengan cepat sebagai bagian dari diskusi atau jika Anda memerlukan distribusi saat menyusun model yang tidak mudah dibuat dari palet yang ada, fungsionalitas freehand berguna. Sesuai namanya, ini memungkinkan Anda menggambar distribusi menggunakan alat melukis sederhana.

Sekarang kita melihat visualisasi distribusi, dengan beberapa parameter di sisi kiri. Simbol mean dan standar deviasi harus terlihat familiar. Dalam kasus distribusi normal, rata-ratanya adalah apa yang sebelumnya kita masukkan sebagai nilai tunggal dalam sel. Berikut adalah distribusi probabilitas penjualan 2018 sebagai contoh, dengan 10% mewakili rata-rata. Sementara model tipikal Anda hanya akan fokus pada angka 10%, atau memiliki skenario "banteng" dan "beruang" dengan pertumbuhan masing-masing mungkin 15% dan 5%, ini sekarang memberikan informasi tentang berbagai hasil potensial yang diharapkan.

Salah satu manfaat simulasi Monte Carlo adalah bahwa hasil ekor dengan probabilitas rendah dapat memicu pemikiran dan diskusi. Hanya menampilkan skenario naik dan turun yang dapat menimbulkan risiko bahwa pembuat keputusan menafsirkannya sebagai batas luar, mengabaikan skenario apa pun yang ada di luar. Hal ini dapat mengakibatkan pengambilan keputusan yang salah, dengan paparan hasil yang berada di luar toleransi organisasi atau individu terhadap risiko. Bahkan probabilitas 5% atau 1% mungkin tidak dapat diterima jika skenario tersebut akan memiliki konsekuensi bencana.

Langkah 3. Memperluas Prakiraan Pendapatan dari Satu Tahun ke Beberapa Tahun

Dengan pemodelan Monte Carlo, perhatikan bagaimana distribusi ketidakpastian dan probabilitas menumpuk satu sama lain, seperti dari waktu ke waktu. Mari kita tinjau sebuah contoh. Karena penjualan di setiap tahun bergantung pada pertumbuhan di tahun-tahun sebelumnya, kami dapat memvisualisasikan dan melihat bahwa perkiraan kami untuk penjualan 2022 lebih tidak pasti daripada untuk 2018 (ditunjukkan dengan menggunakan deviasi standar dan interval kepercayaan 95% di setiap tahun). Demi kesederhanaan, contoh di bawah ini menentukan pertumbuhan untuk satu tahun, 2018, dan kemudian menerapkan tingkat pertumbuhan yang sama untuk setiap tahun berikutnya hingga 2022. Pendekatan lain adalah memiliki lima distribusi independen, satu untuk setiap tahun.

Langkah 4. Melanjutkan Laporan Laba Rugi—Menyatakan Margin sebagai Distribusi Probabilitas

Kami sekarang memperkirakan distribusi probabilitas untuk margin EBIT pada tahun 2018 (disorot di bawah) serupa dengan bagaimana kami melakukannya untuk pertumbuhan penjualan.

Di sini, kita dapat menggunakan fungsi korelasi untuk mensimulasikan situasi di mana ada korelasi yang jelas antara pangsa pasar relatif dan profitabilitas, yang mencerminkan skala ekonomi. Skenario dengan pertumbuhan penjualan yang lebih tinggi relatif terhadap pasar dan dengan demikian pangsa pasar relatif yang lebih tinggi dapat dimodelkan untuk memiliki korelasi positif dengan margin EBIT yang lebih tinggi. Dalam industri di mana kekayaan perusahaan sangat berkorelasi dengan beberapa faktor eksternal lainnya, seperti harga minyak atau nilai tukar mata uang asing, mendefinisikan distribusi untuk faktor tersebut dan memodelkan korelasi dengan penjualan dan profitabilitas dapat masuk akal.

Bergantung pada waktu yang tersedia, ukuran transaksi, dan faktor lainnya, seringkali masuk akal untuk membangun model operasi dan memasukkan variabel yang paling tidak pasti secara eksplisit. Ini termasuk: volume dan harga produk, harga komoditas, kurs FX, item baris overhead utama, pengguna aktif bulanan, dan pendapatan rata-rata per unit (ARPU). Dimungkinkan juga untuk memodelkan di luar variabel jumlah seperti waktu pengembangan, waktu ke pasar, atau tingkat adopsi pasar.

Langkah 5. Neraca dan Laporan Arus Kas

Dengan menggunakan pendekatan yang diuraikan, sekarang kita dapat melanjutkan melalui neraca dan laporan arus kas, diisi dengan asumsi dan menggunakan distribusi probabilitas yang masuk akal.

Catatan tentang belanja modal: ini dapat dimodelkan baik dalam jumlah absolut atau sebagai persentase penjualan, berpotensi dikombinasikan dengan investasi bertahap yang lebih besar; fasilitas manufaktur, misalnya, mungkin memiliki batas kapasitas yang jelas dan investasi ekspansi yang besar atau fasilitas baru yang diperlukan ketika penjualan melebihi ambang batas. Karena masing-masing dari 1.000 atau 10.000 iterasi tersebut akan menjadi perhitungan ulang model yang lengkap, formula sederhana yang memicu biaya investasi jika/ketika volume tertentu tercapai dapat digunakan.

Langkah 6. Menyelesaikan Model

Membangun model Monte Carlo memiliki satu langkah tambahan dibandingkan dengan model keuangan standar: Sel tempat kita ingin mengevaluasi hasil harus secara khusus ditetapkan sebagai sel keluaran. Perangkat lunak akan menyimpan hasil setiap iterasi simulasi untuk sel-sel tersebut untuk kami evaluasi setelah simulasi selesai. Semua sel di seluruh model dihitung ulang dengan setiap iterasi, tetapi hasil iterasi di sel lain, yang tidak ditetapkan sebagai sel input atau output, hilang dan tidak dapat dianalisis setelah simulasi selesai. Seperti yang Anda lihat pada tangkapan layar di bawah, kami menetapkan sel hasil MIRR sebagai sel keluaran.

Setelah Anda selesai membangun model, sekarang saatnya untuk menjalankan simulasi untuk pertama kalinya hanya dengan menekan "mulai simulasi" dan menunggu beberapa detik.

Langkah 7. Menafsirkan Hasil

Output Dinyatakan sebagai Probabilitas. Sementara model kami sebelumnya memberi kami nilai tunggal untuk IRR yang dimodifikasi, kami sekarang dapat dengan jelas melihat bahwa ada sejumlah hasil potensial di sekitar nilai itu, dengan probabilitas yang berbeda. Ini memungkinkan kami untuk menyusun ulang pertanyaan, seperti "Apakah kami akan mencapai tingkat pengembalian rintangan kami dengan investasi ini?" menjadi “Seberapa besar kemungkinan kita untuk mencapai atau melampaui tingkat rintangan kita?” Anda dapat menjelajahi hasil mana yang paling mungkin menggunakan, misalnya, interval kepercayaan. Visualisasi sangat membantu saat mengkomunikasikan hasil kepada pemangku kepentingan yang berbeda, dan Anda dapat melapisi keluaran dari transaksi lain untuk membandingkan secara visual seberapa menarik dan (tidak)pasti transaksi saat ini dibandingkan dengan transaksi lainnya (lihat di bawah).

Memahami tingkat ketidakpastian dalam hasil akhir. Jika kita menghasilkan bagan variabilitas arus kas dari waktu ke waktu, mirip dengan apa yang kita lakukan pada awalnya untuk penjualan, menjadi jelas bahwa variabilitas dalam arus kas bebas menjadi signifikan bahkan dengan ketidakpastian yang relatif kecil dalam penjualan dan input lain yang kita modelkan sebagai distribusi probabilitas. , dengan hasil berkisar antara €0,5 juta hingga €5,0 juta—faktor 10x—bahkan hanya satu standar deviasi dari rata-rata. Ini adalah hasil dari menumpuknya asumsi yang tidak pasti di atas satu sama lain, efek yang menggabungkan baik "vertikal" selama bertahun-tahun, dan "horizontal" ke bawah melalui laporan keuangan. Visualisasi memberikan informasi tentang kedua jenis ketidakpastian.

Analisis sensitivitas: Memperkenalkan grafik tornado. Area penting lainnya adalah memahami input mana yang memiliki dampak terbesar pada hasil akhir Anda. Sebuah contoh klasik adalah bagaimana pentingnya tingkat diskonto atau asumsi nilai terminal sering diberikan bobot yang terlalu kecil dibandingkan dengan peramalan arus kas. Salah satu cara umum untuk menangani ini adalah dengan menggunakan matriks di mana Anda meletakkan satu input kunci pada setiap sumbu dan kemudian menghitung hasilnya di setiap sel (lihat di bawah). Ini berguna terutama dalam situasi di mana keputusan bergantung pada satu atau beberapa asumsi kunci—dalam situasi “apa yang harus Anda percayai” ini, pembuat keputusan (misalnya) komite investasi atau tim manajemen senior mungkin memiliki pandangan yang berbeda tentang asumsi kunci tersebut, dan matriks seperti di atas memungkinkan masing-masing dari mereka untuk menemukan nilai hasil yang sesuai dengan pandangan mereka, dan dapat memutuskan, memilih, atau memberikan saran berdasarkan itu.

Meningkatkan dengan simulasi Monte Carlo. Saat menggunakan simulasi Monte Carlo, pendekatan tersebut dapat dilengkapi dengan yang lain: diagram tornado. Visualisasi ini mencantumkan input dan asumsi yang tidak pasti yang berbeda pada sumbu vertikal dan kemudian menunjukkan seberapa besar dampak masing-masing pada hasil akhir.

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein