Caseta de instrumente a prognozatorului: Cum se efectuează simulări Monte Carlo

Rezumat

Introducere

În primul rând, singura certitudine este că nu există nicio certitudine. În al doilea rând, fiecare decizie ca o consecință este o chestiune de cântărire a probabilităților. În al treilea rând, în ciuda incertitudinii, trebuie să decidem și trebuie să acționăm. Și, în sfârșit, trebuie să judecăm deciziile nu numai în funcție de rezultate, ci și de modul în care au fost luate acele decizii. – Robert E. Rubin

Unul dintre cele mai importante și provocatoare aspecte ale prognozei este gestionarea incertitudinii inerente examinării viitorului. După ce am construit și populat sute de modele financiare și operaționale pentru LBO, strângeri de fonduri pentru startup, bugete, fuziuni și achiziții și planuri strategice corporative din 2003, am asistat la o gamă largă de abordări pentru a face acest lucru. Fiecare CEO, CFO, membru al consiliului de administrație, investitor sau membru al comitetului de investiții își aduce propria experiență și abordare față de proiecțiile financiare și incertitudinea, influențată de diferite stimulente. Adesea, compararea rezultatelor reale cu proiecțiile oferă o apreciere a cât de mari pot fi abaterile dintre previziuni și rezultatele reale și, prin urmare, necesitatea de a înțelege și de a recunoaște în mod explicit incertitudinea.

Inițial, am început să folosesc analizele de scenarii și de sensibilitate pentru a modela incertitudinea și le consider în continuare instrumente foarte utile. De când am adăugat simulări Monte Carlo la setul meu de instrumente în 2010, am descoperit că acestea sunt un instrument extrem de eficient pentru a perfecționa și a îmbunătăți modul în care gândiți riscurile și probabilitățile. Am folosit abordarea pentru orice, de la construirea evaluărilor DCF, evaluarea opțiunilor de apel în fuziuni și achiziții și discutarea riscurilor cu creditorii până la căutarea de finanțare și îndrumarea alocarii fondurilor de capital de risc pentru startup-uri. Abordarea a fost întotdeauna bine primită de membrii consiliului de administrație, investitori și echipele de conducere. În acest articol, ofer un tutorial pas cu pas despre utilizarea simulărilor Monte Carlo în practică prin construirea unui model de evaluare DCF.

Fiecare decizie este o chestiune de cântărire a probabilităților

Înainte de a începe cu studiul de caz, să trecem în revistă câteva abordări diferite pentru gestionarea incertitudinii. Conceptul de valoare așteptată — media ponderată în funcție de probabilitate a fluxurilor de numerar în toate scenariile posibile — este Finanțe 101. Dar profesioniștii din domeniul finanțelor și, mai larg, factorii de decizie, adoptă abordări foarte diferite atunci când traduc această perspectivă simplă în practică. Abordarea poate varia de la pur și simplu nerecunoașterea sau discutarea incertitudinii, pe de o parte, până la modele și software sofisticate, pe de altă parte. În unele cazuri, oamenii ajung să petreacă mai mult timp discutând despre probabilități decât calculând fluxurile de numerar.

Pe lângă faptul că pur și simplu nu o abordăm, să examinăm câteva modalități de a gestiona incertitudinea în proiecțiile pe termen mediu sau lung. Multe dintre acestea ar trebui să vă fie familiare.

Crearea unui singur scenariu. Această abordare este implicită pentru bugete, multe startup-uri și chiar decizii de investiții. Pe lângă faptul că nu conține nicio informație despre gradul de incertitudine sau recunoașterea faptului că rezultatele pot diferi de proiecții, aceasta poate fi ambiguă și poate fi interpretată diferit în funcție de părțile interesate. Unii îl pot interpreta ca o țintă întinsă, în care rezultatul real este mai probabil să scadă sub decât să depășească. Unii o văd ca pe o performanță de bază cu mai mult avantaj decât dezavantaj. Alții îl pot vedea ca un „caz de bază” cu o probabilitate de 50/50 în sus și în jos. În unele abordări, în special pentru startup-uri, este foarte ambițios și eșecul sau deficitul este de departe cel mai probabil rezultatul, dar o rată de actualizare mai mare este utilizată în încercarea de a ține seama de risc.	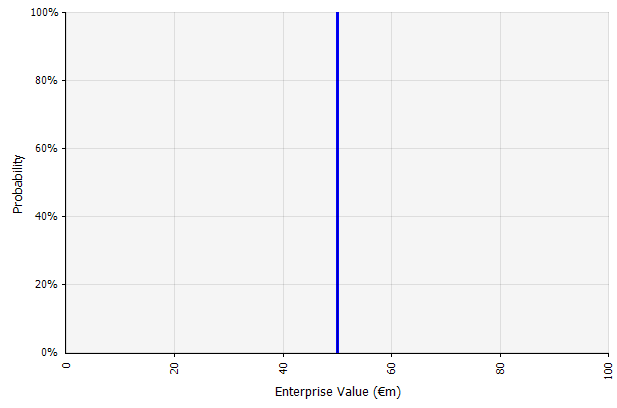Intrările în prognoza fluxului de numerar pe termen lung conform acestei abordări sunt toate estimări punctuale, producând un rezultat estimativ punctual de 50 milioane EUR în acest exemplu, cu o probabilitate implicită de 100%.
Crearea mai multor scenarii. Această abordare recunoaște că realitatea este puțin probabil să se desfășoare conform unui singur plan dat. 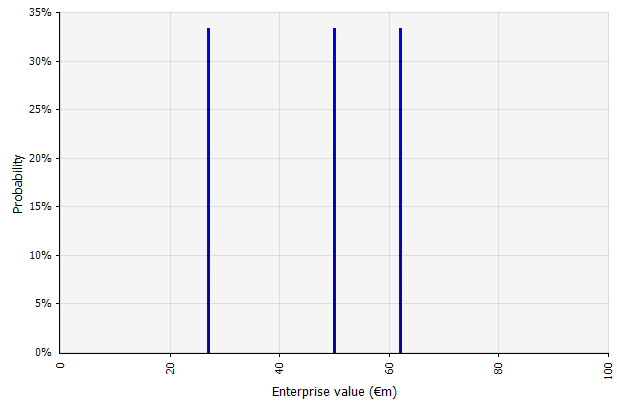În cea mai simplă formă, analiza de sensibilitate, aceasta ar putea simula impactul, de exemplu, al creșterii vânzărilor cu 10% peste și sub cel al cazului de bază, folosind un amestec dat de costuri fixe, semivariabile și variabile pentru a estima rezultatul final. impact. În forme mai complexe, te gândești la viitor dintr-o perspectivă complet diferită pentru fiecare scenariu și analizezi impactul pe care evoluțiile tehnologice diferite, dinamica competitivă și tendințele macro îl vor avea asupra performanței companiei. Deseori, scenariile sunt alese, din păcate, destul de arbitrar și uneori având în vedere un rezultat final dorit.	Cele trei scenarii diferite dau trei rezultate diferite, aici presupuse a fi la fel de probabile. Probabilitățile de rezultate în afara scenariilor ridicate și scăzute nu sunt luate în considerare.
Crearea de cazuri de bază, pozitive și negative cu probabilități recunoscute în mod explicit. Adică, cazurile de urs și bull conțin, de exemplu, o probabilitate de 25% în fiecare coadă, iar estimarea valorii juste reprezintă punctul de mijloc. Un beneficiu util al acestui lucru din perspectiva managementului riscului este analiza explicită a riscului de coadă, adică evenimentele din afara scenariilor de creștere și dezavantaje.	Ilustrație din Manualul de evaluare Morningstar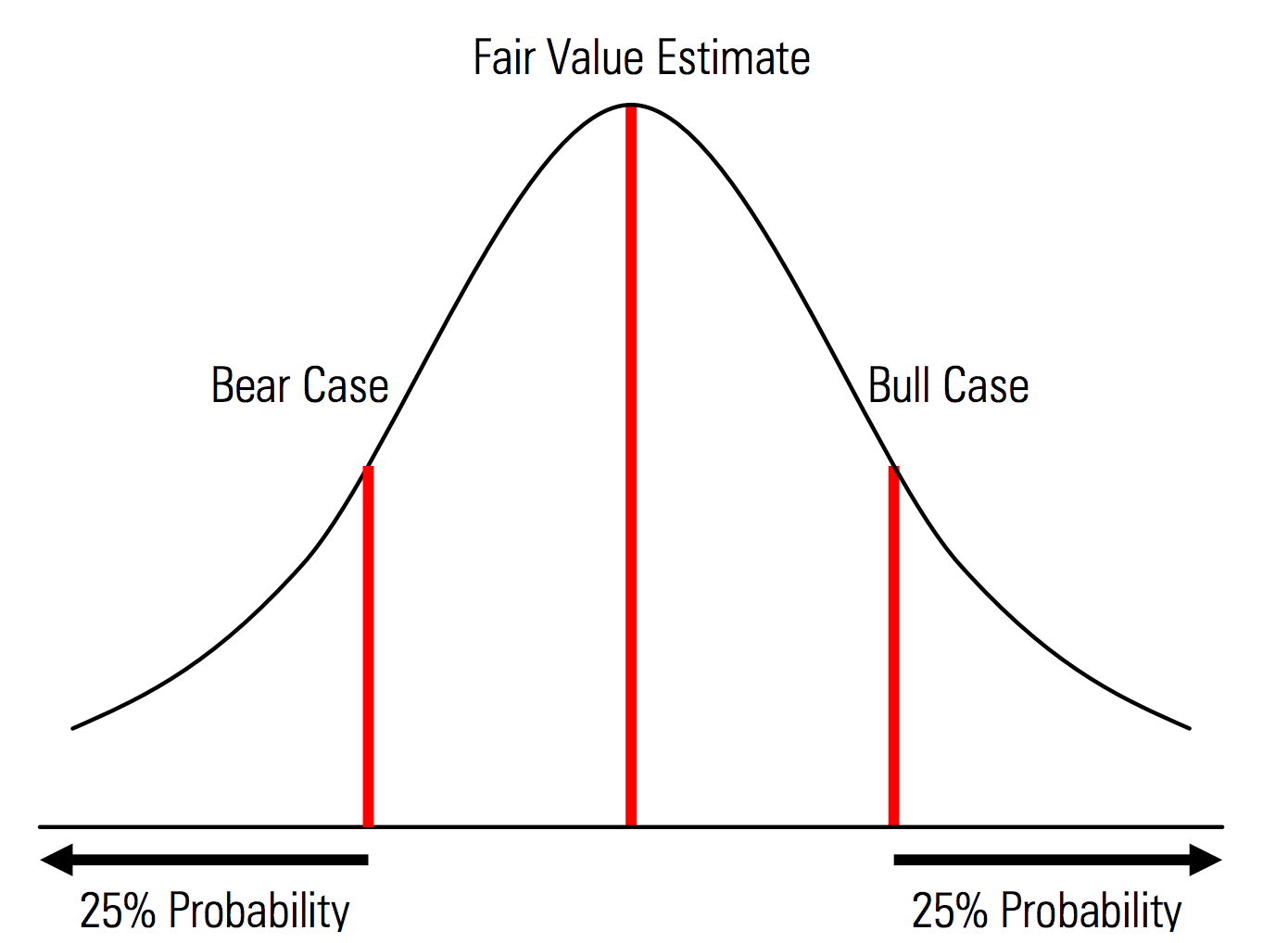
Folosind distribuții de probabilitate și simulări Monte Carlo. Utilizarea distribuțiilor de probabilitate vă permite să modelați și să vizualizați întreaga gamă de rezultate posibile în prognoză. Acest lucru se poate face nu numai la nivel agregat, ci și pentru intrări individuale detaliate, ipoteze și factori. Metodele Monte Carlo sunt apoi utilizate pentru a calcula distribuțiile de probabilitate rezultate la un nivel agregat, permițând analiza modului în care mai multe variabile incerte contribuie la incertitudinea rezultatelor generale. Poate cel mai important, abordarea îi obligă pe toți cei implicați în analiză și decizie să recunoască în mod explicit incertitudinea inerentă prognozării și să gândească în probabilități. La fel ca și celelalte abordări, aceasta are dezavantajele sale, inclusiv riscul de precizie falsă și excesul de încredere care ar putea rezulta odată cu utilizarea unui model mai sofisticat și munca suplimentară necesară pentru a selecta distribuțiile de probabilitate adecvate și estimarea parametrilor acestora, acolo unde altfel ar fi doar estimări punctuale. folosit.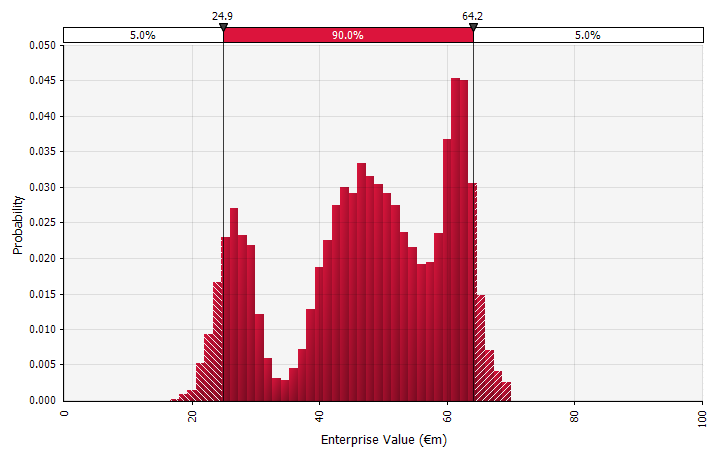

Ce este o simulare Monte Carlo?

Simulările Monte Carlo modelează probabilitatea unor rezultate diferite în previziunile și estimările financiare. Ei își câștigă numele din zona Monte Carlo din Monaco, care este renumită în întreaga lume pentru cazinourile sale de lux; rezultatele aleatorii sunt esențiale pentru tehnică, la fel ca și pentru ruleta și aparatele de slot. Simulările Monte Carlo sunt utile într-o gamă largă de domenii, inclusiv inginerie, management de proiect, explorare de petrol și gaze și alte industrii cu capital intensiv, cercetare și dezvoltare și asigurări; aici, mă concentrez pe aplicații în finanțe și afaceri.

Distribuții de probabilitate

În simulare, intrările incerte sunt descrise folosind distribuții de probabilitate, descrise prin parametri precum media și abaterea standard. Exemple de intrări în proiecțiile financiare ar putea fi orice, de la venituri și marje la ceva mai granular, cum ar fi prețurile mărfurilor, cheltuielile de capital pentru o expansiune sau ratele de schimb valutar.

Când una sau mai multe intrări sunt descrise ca distribuții de probabilitate, rezultatul devine, de asemenea, o distribuție de probabilitate. Un computer extrage aleatoriu un număr din fiecare distribuție de intrare și calculează și salvează rezultatul. Acest lucru se repetă de sute, mii sau zeci de mii de ori, fiecare numită iterație. Luate împreună, aceste iterații aproximează distribuția de probabilitate a rezultatului final.

Tipuri de intrări

Distribuțiile de intrare pot fi fie continue , unde valoarea generată aleatoriu poate lua orice valoare sub distribuție (de exemplu, o distribuție normală), fie discrete , unde probabilitățile sunt atașate la două sau mai multe scenarii distincte.

O simulare poate conține, de asemenea, un amestec de distribuții de diferite tipuri. Luați, de exemplu, un proiect de cercetare-dezvoltare în domeniul farmaceutic cu mai multe etape, fiecare având o probabilitate discretă de succes sau eșec. Acest lucru poate fi combinat cu distribuții continue care descriu sume de investiții incerte necesare pentru fiecare etapă și venituri potențiale dacă proiectul are ca rezultat un produs care ajunge pe piață. Graficul de mai jos arată rezultatul unei astfel de simulări: o probabilitate de ~65% de a pierde întreaga investiție de la 5 milioane EUR până la 50 milioane EUR (valoare actuală) și o probabilitate de ~35% de un câștig net cel mai probabil în intervalul de 100 EUR până la 250 EUR — informații care s-ar pierde dacă valorile cheie de ieșire, cum ar fi MIRR sau NPV, sunt afișate ca estimări punctuale, mai degrabă decât distribuții de probabilitate.

Simulari Monte Carlo în practică

Unul dintre motivele pentru care simulările Monte Carlo nu sunt utilizate pe scară largă este că instrumentele obișnuite de finanțare de zi cu zi nu le suportă foarte bine. Excel și Google Sheets dețin un număr sau un rezultat de formulă în fiecare celulă și, deși pot defini distribuții de probabilitate și pot genera numere aleatorii, construirea de la zero a unui model financiar cu funcționalitatea Monte Carlo este greoaie. Și, în timp ce multe instituții financiare și firme de investiții folosesc simulări Monte Carlo pentru evaluarea instrumentelor derivate, analiza portofoliilor și multe altele, instrumentele lor sunt dezvoltate în mod obișnuit intern, proprietare sau prohibitiv de costisitoare, făcându-le inaccesibile pentru profesioniștii în finanțe individuale.

Astfel, vreau să atrag atenția asupra pluginurilor Excel precum @RISK by Palisade, ModelRisk by Vose și RiskAMP, care simplifică foarte mult lucrul cu simulările Monte Carlo și vă permit să le integrați în modelele existente. În următoarea explicație, voi folosi @RISK.

Studiu de caz: Cash Flow Projections cu Monte Carlo Simulation

Să trecem în revistă un exemplu simplu care ilustrează conceptele cheie ale unei simulări Monte Carlo: o prognoză a fluxului de numerar pe cinci ani. În acest tutorial, am configurat și populez un model de flux de numerar de bază în scopuri de evaluare, am înlocuit treptat intrările cu distribuții de probabilitate și, în final, rulez simularea și analizez rezultatele.

Pasul 1. Alegerea sau construirea modelului

Pentru început, folosesc un model simplu, axat pe evidențierea caracteristicilor cheie ale utilizării distribuțiilor de probabilitate. Rețineți că, pentru început, acest model nu este diferit de orice alt model Excel; pluginurile pe care le-am menționat mai sus funcționează cu modelele și foile de calcul existente. Modelul de mai jos este o versiune simplă, completă cu ipoteze pentru a forma un singur scenariu.

Pasul 2. Crearea primei distribuții de probabilitate

În primul rând, trebuie să colectăm informațiile necesare pentru a face ipotezele noastre, apoi trebuie să alegem distribuțiile de probabilitate corecte pe care să le inserăm. Este important să rețineți că sursa intrărilor/ipotezelor cheie este aceeași, indiferent de abordarea pe care o luați pentru a gestiona incertitudinea. Due diligence comerciale, o revizuire cuprinzătoare a planului de afaceri al companiei în contextul dezvoltării pieței proiectate, al tendințelor industriei și al dinamicii concurenței, include de obicei extrapolarea din date istorice, încorporarea opiniilor experților, efectuarea de cercetări de piață și intervievarea participanților de pe piață. Din experiența mea, experții și participanții la piață sunt bucuroși să discute diferite scenarii, riscuri și game de rezultate. Cu toate acestea, majoritatea nu descriu în mod explicit distribuțiile de probabilitate.

Să trecem acum prin și să înlocuim valorile noastre cheie de intrare cu distribuții de probabilitate una câte una, începând cu creșterea estimată a vânzărilor pentru primul an de prognoză (2018). Pluginul @RISK pentru Excel poate fi evaluat cu o probă gratuită de 15 zile, astfel încât să îl puteți descărca de pe site-ul Palisade și să îl instalați cu câteva clicuri. Cu pluginul @RISK activat, selectați celula în care doriți distribuția și selectați „Definiți distribuția” în meniu.

Apoi selectați unul din paleta de distribuții care apare. Software-ul @RISK oferă peste 70 de distribuții diferite din care să alegeți, așa că alegerea uneia poate părea copleșitoare la început. Mai jos este un ghid pentru o mână pe care o folosesc cel mai des:

Normal. Definit prin medie și deviația standard. Acesta este un bun punct de plecare datorită simplității sale și potrivit ca o extensie a abordării Morningstar, în care definiți o distribuție care acoperă probabil scenarii sau intervale deja definite pentru o anumită intrare, asigurându-vă că cazurile sunt simetrice în jurul cazului de bază și că probabilitățile din fiecare coadă par rezonabile (să zicem 25% ca în exemplul Morningstar).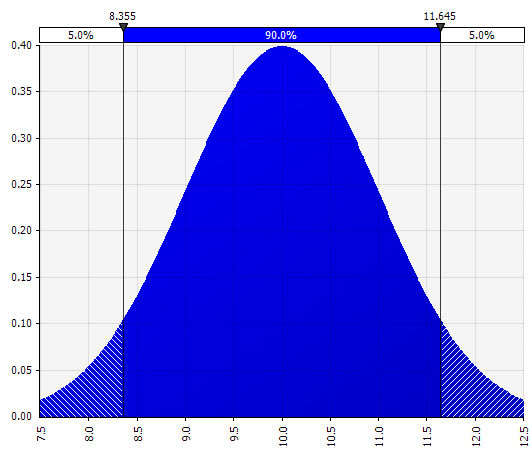
Momente Johnson. Alegerea acestui lucru vă permite să definiți distribuții și distribuții distorsionate cu cozi mai grase sau mai subțiri (adăugând din punct de vedere tehnic parametrii de asimetrie și curtoză). În culise, acesta folosește un algoritm pentru a alege una dintre cele patru distribuții care reflectă cei patru parametri aleși, dar care este invizibil pentru utilizator --- tot ce trebuie să ne concentrăm sunt parametrii. Uneori, în procesul de culegere a informațiilor pentru intrare, devine clar că distribuția normală nu este adecvată. De exemplu, pentru o companie aflată la pragul sau vârful unui ciclu industrial, probabilitățile de performanță mai bună sau mai slabă în următorii, să zicem, cinci ani, nu vor fi simetrice. Cu cât este mai aproape de vârf, cu atât este mai probabilă o scădere față de o performanță puternică continuă. Aici poate fi utilă o distribuție oblică. S-au scris multe despre conceptul de „cozi grase” în multe domenii ale finanțelor. Se pare că distribuția normală adesea nu descrie foarte bine rezultatele reale, evenimentele care ar trebui să fie foarte rare apar mai frecvent decât ar indica o distribuție normală.
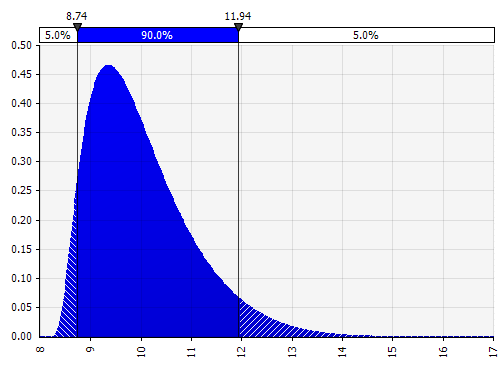Discret. Acolo unde probabilitățile sunt date la două sau mai multe valori specifice. Revenind la exemplul proiectului R&D în etape de la început, probabilitatea de succes în fiecare etapă este modelată ca o distribuție binară discretă, cu un rezultat de 1 reprezentând succesul și 0 eșec.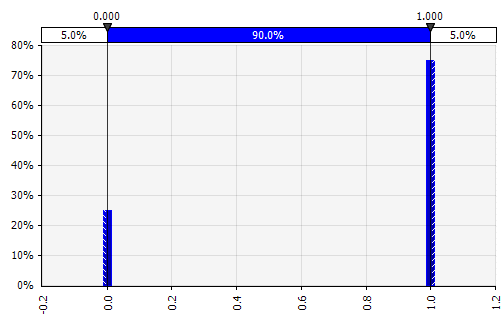
Montaj de distribuție. Când aveți o cantitate mare de puncte de date istorice, funcționalitatea de potrivire a distribuției este utilă. Acest lucru nu înseamnă trei sau patru ani de creștere istorică a vânzărilor, de exemplu, ci date din seria temporală, cum ar fi prețurile mărfurilor, cursurile de schimb valutar sau alte prețuri de piață, în care istoria poate oferi informații utile despre tendințele viitoare și gradul de incertitudine.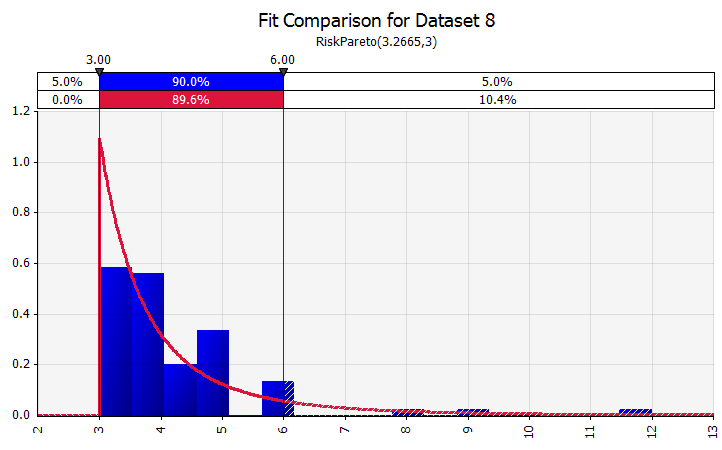
Combinând mai multe distribuții diferite într-una singură. Pentru a atenua impactul potențial al prejudecăților individuale, este adesea o idee bună să încorporăm contribuțiile diferitelor surse într-o ipoteză și/sau să revizuim și să discutăm rezultatele. Există diferite abordări: 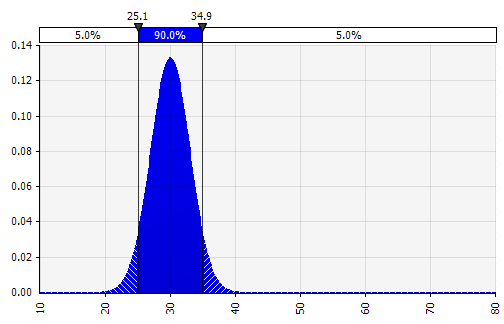Pregătiți o schiță sau o primă vizualizare și apoi revizuiți-l cu experți, echipa de management mai largă sau alți factori de decizie. Dezvoltați cele mai importante distribuții în comun într-o întâlnire. Acest lucru poate duce la o discuție bună și la rezultate mai bune, dar, ca întotdeauna, componența grupului este critică; a avea diferite perspective/funcții reprezentate și a promova o atmosferă de dezbatere viguroasă, dar respectuoasă, sunt desigur utile. Dezvoltați o distribuție pentru fiecare sursă cheie și combinați-le, ponderate în funcție de cât de multă încredere aveți în fiecare. Dacă primiți contribuții de la mai mulți experți diferiți, poate fi o idee bună să-i lăsați pe fiecare dintre ei să-și ofere propria viziune, independent de ceilalți, și apoi să se combine într-unul singur. Funcția @RISK MakeRiskInput face acest lucru pentru noi.	Greutate: 20% 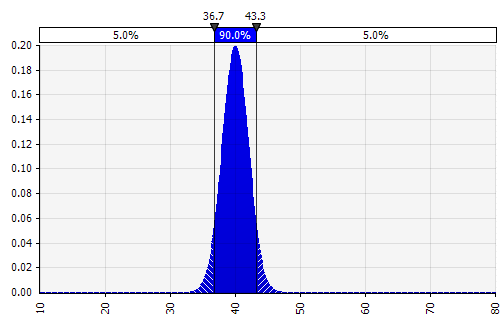+ Greutate: 20% 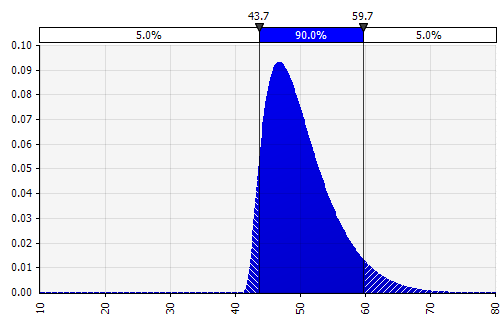+ Greutate: 60% =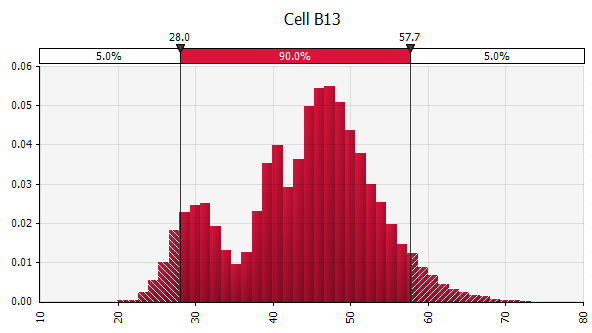
Mână liberă. Pentru a ilustra rapid o distribuție ca parte a discuțiilor sau dacă aveți nevoie de o distribuție atunci când creați un model care nu este ușor de creat din paleta existentă, funcționalitatea cu mână liberă este utilă. După cum sugerează și numele, acest lucru vă permite să desenați distribuția folosind un instrument simplu de pictură.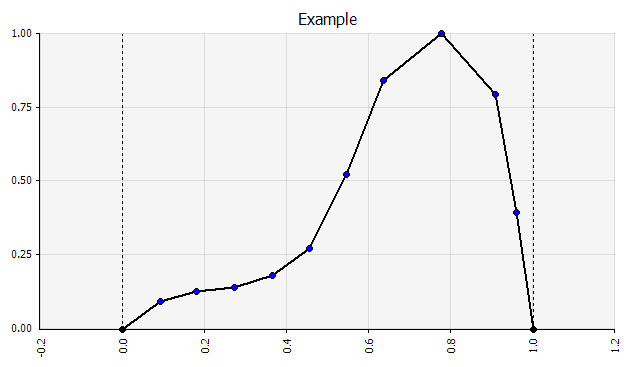

Acum vedem o vizualizare a distribuției, cu câțiva parametri în partea stângă. Simbolurile medie și deviația standard ar trebui să pară familiare. În cazul unei distribuții normale, media ar fi ceea ce am introdus anterior ca valoare unică în celulă. Iată, ca exemplu, distribuția probabilității vânzărilor din 2018, cu 10% reprezentând media. În timp ce modelul dvs. obișnuit fie s-ar concentra doar pe cifra de 10%, fie ar avea scenarii „taur” și „urs” cu probabil o creștere de 15% și, respectiv, 5%, acesta oferă acum informații despre întreaga gamă de rezultate potențiale așteptate.

Un beneficiu al simulărilor Monte Carlo este că rezultatele cu probabilitate scăzută pot declanșa gândirea și discuțiile. Numai afișarea scenariilor pozitive și negative poate introduce riscul ca factorii de decizie să le interpreteze ca limite exterioare, respingând orice scenarii care se află în exterior. Acest lucru poate duce la luarea deciziilor greșite, cu expunerea la rezultate care se află dincolo de toleranța organizației sau a individului la risc. Chiar și o probabilitate de 5% sau 1% poate fi inacceptabilă dacă scenariul în cauză ar avea consecințe catastrofale.

Pasul 3. Extinderea prognozei veniturilor de la un an la mai mulți

Cu modelarea Monte Carlo, fiți atenți la modul în care distribuțiile de incertitudine și de probabilitate se stivuiesc una peste alta, cum ar fi în timp. Să trecem în revistă un exemplu. Întrucât vânzările din fiecare an depind de creșterea din anii precedenți, putem vizualiza și vedea că estimarea noastră a vânzărilor din 2022 este mai incertă decât cea pentru 2018 (indicată folosind abaterile standard și intervalele de încredere de 95% în fiecare an). Din motive de simplitate, exemplul de mai jos specifică creșterea pentru un an, 2018, și apoi aplică aceeași rată de creștere pentru fiecare dintre următorii ani până în 2022. O altă abordare este de a avea cinci distribuții independente, câte una pentru fiecare an.

Pasul 4. Continuarea în jos a Declarației de venit—Exprimarea marjelor ca distribuții de probabilitate

Acum estimăm o distribuție a probabilității pentru marja EBIT în 2018 (evidențiată mai jos), în mod similar cu modul în care am făcut-o pentru creșterea vânzărilor.

Aici, putem folosi funcția de corelare pentru a simula o situație în care există o corelație clară între cota relativă de piață și profitabilitate, reflectând economiile de scară. Scenariile cu o creștere mai mare a vânzărilor în raport cu piața și, în mod corespunzător, o cotă relativă mai mare de piață pot fi modelate pentru a avea o corelație pozitivă cu marje EBIT mai mari. În industriile în care averea unei firme este strâns corelată cu un alt factor extern, cum ar fi prețul petrolului sau cursul valutar, definirea unei distribuții pentru acel factor și modelarea unei corelații cu vânzările și profitabilitatea poate avea sens.

În funcție de timpul disponibil, dimensiunea tranzacției și alți factori, este adesea logic să construim un model de operare și să introduceți în mod explicit cele mai incerte variabile. Acestea includ: volumele și prețurile produselor, prețurile mărfurilor, ratele valutare, elementele linii generale cheie, utilizatorii activi lunari și venitul mediu pe unitate (ARPU). De asemenea, este posibil să se modeleze dincolo de variabilele de cantitate, cum ar fi timpul de dezvoltare, timpul de lansare pe piață sau rata de adoptare pe piață.

Pasul 5. Bilanțul și situația fluxului de numerar

Folosind abordarea prezentată, putem continua acum prin bilanțul și situația fluxurilor de numerar, completând cu ipoteze și utilizând distribuții de probabilitate acolo unde are sens.

O notă despre capex: aceasta poate fi modelată fie în sume absolute, fie ca procent din vânzări, potențial în combinație cu investiții mai mari în trepte; o unitate de producție poate avea, de exemplu, o limită clară a capacității și o investiție mare de extindere sau o nouă instalație necesară atunci când vânzările depășesc pragul. Întrucât fiecare dintre cele 1.000 sau 10.000 de iterații, să zicem, va fi o recalculare completă a modelului, se poate folosi o formulă simplă care declanșează costul investiției dacă/când este atins un anumit volum.

Pasul 6. Finalizarea modelului

Construirea unui model Monte Carlo are un pas suplimentar în comparație cu un model financiar standard: celulele în care dorim să evaluăm rezultatele trebuie să fie desemnate în mod specific ca celule de ieșire. Software-ul va salva rezultatele fiecărei iterații a simulării pentru acele celule pentru ca noi să le evaluăm după ce simularea este terminată. Toate celulele din întregul model sunt recalculate cu fiecare iterație, dar rezultatele iterațiilor din alte celule, care nu sunt desemnate ca celule de intrare sau de ieșire, se pierd și nu pot fi analizate după terminarea simulării. După cum puteți vedea în captura de ecran de mai jos, desemnăm celula rezultat MIRR ca o celulă de ieșire.

Odată ce ați terminat de construit modelul, este timpul să rulați simularea pentru prima dată, apăsând pur și simplu „start simulation” și așteptând câteva secunde.

Pasul 7. Interpretarea rezultatelor

Ieșiri exprimate ca probabilități. În timp ce modelul nostru anterior ne dădea o singură valoare pentru IRR modificată, acum putem vedea clar că există o serie de rezultate potențiale în jurul valorii respective, cu probabilități diferite. Acest lucru ne permite să reformulăm întrebări, cum ar fi „Vom atinge rata de returnare a obstacolelor noastre cu această investiție?” la „Cât de probabil avem să ne atingem sau să depășim rata de obstacole?” Puteți explora ce rezultate sunt cel mai probabil folosind, de exemplu, un interval de încredere. Vizualizarea este utilă atunci când comunicați rezultatele diferitelor părți interesate și puteți suprapune rezultate din alte tranzacții pentru a compara vizual cât de atractiv și (ne)sigur este cea actuală în comparație cu altele (vezi mai jos).

Înțelegerea gradului de incertitudine în rezultatul final. Dacă generăm o diagramă a variabilității fluxului de numerar în timp, similar cu ceea ce am făcut inițial pentru vânzări, devine clar că variabilitatea fluxului de numerar liber devine semnificativă chiar și cu o incertitudine relativ modestă în vânzări și alte inputuri pe care le-am modelat ca distribuții de probabilitate. , cu rezultate variind de la aproximativ 0,5 milioane EUR până la 5,0 milioane EUR — un factor de 10 ori — chiar și doar o abatere standard de la medie. Acesta este rezultatul stivuirii ipotezelor incerte una peste alta, un efect care se agravează atât „vertical” de-a lungul anilor, cât și „orizontal” în jos prin situațiile financiare. Vizualizările oferă informații despre ambele tipuri de incertitudine.

Analiza de sensibilitate: Prezentarea graficului tornadei. Un alt domeniu important este să înțelegeți care intrări au cel mai mare impact asupra rezultatului final. Un exemplu clasic este modul în care importanța ratei de actualizare sau a ipotezelor privind valoarea terminală este adesea acordată prea puțină pondere în raport cu prognoza fluxului de numerar. O modalitate obișnuită de a gestiona acest lucru este utilizarea matricelor în care puneți o intrare cheie pe fiecare axă și apoi calculați rezultatul în fiecare celulă (vezi mai jos). Acest lucru este util mai ales în situațiile în care deciziile depind de una sau câteva ipoteze cheie — în aceste situații „ce trebuie să credeți”, factorii de decizie din (de exemplu) un comitet de investiții sau o echipă de conducere superioară pot avea opinii diferite despre acele ipoteze cheie și o matrice precum cea de mai sus permite fiecăruia dintre ei să găsească o valoare a rezultatului corespunzătoare punctului de vedere și poate decide, vota sau da sfaturi pe baza acesteia.

Îmbunătățirea cu simulări Monte Carlo. Când se utilizează simulări Monte Carlo, această abordare poate fi completată cu o alta: diagrama tornadei. Această vizualizare listează diferitele intrări și ipoteze incerte pe axa verticală și apoi arată cât de mare este impactul fiecăreia asupra rezultatului final.

This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.

Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.

A Few Words of Caution: Different Types of Uncertainty

Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb

It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.

In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.

The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.

In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.

At the End of the Day, It's about the Mindset, Not the Technical Solution

There are two concepts here and it is important to separate them: one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it: Monte Carlo simulations in spreadsheets.

I don't use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.

Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.

I spend 98% of my time on 2% probabilities – Lloyd Blankfein