Python教程中的馬爾可夫鏈

概述

你有沒有想過專家氣象學家如何準確預測天氣或谷歌如何對不同的網頁進行排名？ 他們如何在現實世界中製作迷人的 Python 應用程序。 這些計算很複雜，涉及多個動態變量，可以使用概率估計來解決。

這就是馬爾可夫鏈的想法； 有個別狀態（例如，天氣狀況），每個狀態可以隨機變為其他狀態（下雨天可以變為晴天），這些變化或轉換是基於概率的。 本文簡要介紹了馬爾可夫鏈的概念，以及如何利用Python 馬爾可夫鏈在 Python 中編寫馬爾可夫鏈模型來解決實際問題。 如果您是初學者並且想獲得數據科學方面的專業知識，請查看我們的數據科學課程。

內容概述

• 簡單介紹一下馬爾可夫鍊和馬爾可夫性質的概念
• 馬爾可夫鏈的數學和圖形表達
• Python Markov Chain – 用 Python 編寫 Markov Chain 示例

馬爾可夫鏈簡介

要使用Python 馬爾可夫鏈解決實際問題，必須掌握馬爾可夫鏈的概念。 1906 年，俄羅斯數學家安德烈·馬爾科夫給出了馬爾可夫鏈的定義——一個由隨機變量組成的隨機過程，這些變量從一個特定狀態過渡到下一個特定狀態，這些過渡基於特定的假設和概率規則。

稱為馬爾可夫屬性的基本數學屬性是隨機變量轉換的基礎。 換句話說，馬爾可夫鍊是一系列滿足馬爾可夫性質的變量 X1、X2、X3……。

馬爾可夫鏈原理——馬爾可夫性質

馬爾可夫鏈基於馬爾可夫屬性。 離散時間馬爾可夫特性理論指出，隨機系統從一個特定狀態變為下一個過渡狀態的概率僅取決於當前狀態和時間，與之前的狀態無關。

隨機過程的可能未來狀態與之前存在的狀態序列無關，這一事實使馬爾可夫鏈成為僅依賴於變量當前狀態的無記憶過程。

閱讀： Python 中的內置數據結構

馬爾可夫鏈的數學表達式

就概率分佈而言，假設一個系統在時間實例“n”。 應用馬爾可夫性質原理，下一個時間實例 n+1 的狀態條件分佈與系統在時間實例 1、2、…、n-1 的狀態無關。

馬爾可夫鏈的圖形表示

有向圖通常用於表示馬爾可夫鏈。 在有向圖中，節點表示隨機變量的不同可能狀態，而邊表示系統在下一個時間實例中從一種狀態移動到另一種狀態的概率。 為了理解表示，讓我們以預測天氣為例。 假設隨機變量是“天氣”，它具有三種可能的狀態，即。 天氣 = {晴天、下雨、下雪}。 此場景的馬爾可夫鏈可以表示為：

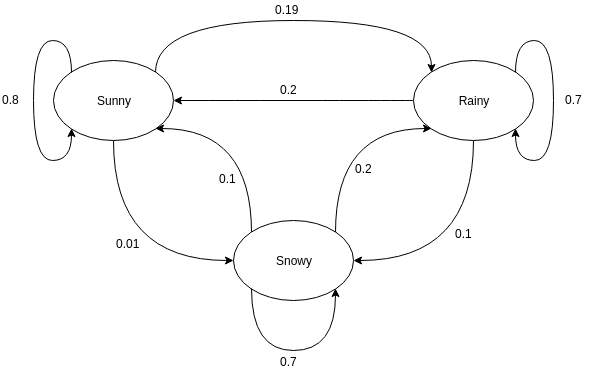
資源

在上面顯示的圖形表示中，假設隨機變量的當前觀察狀態是晴天。 隨機變量在下一次實例中取值為 Sunny 的概率為 0.8。 它也可以以 0.01 的概率取值 snowy，或以 0.19 的概率取值 rainy。 這裡要注意的重要一點是，一個狀態中存在的概率值總和總是為 1。

用 Python 編寫馬爾可夫鏈

為了更好地理解Python 馬爾可夫鏈，讓我們來看一個用 Python 編寫馬爾可夫鏈示例的實例。 在解決現實世界中的問題時，通常的做法是使用有效編碼馬爾可夫鏈的庫。 然而，用 Python 編碼馬爾可夫鍊是開始馬爾可夫鏈分析和模擬的絕佳方式。 因此出現了Python Markov Chain的實用程序。 讓我們看看如何用 Python 編寫上一節中給出的天氣預報示例。 首先定義一個簡單的類：

在定義了 MarkovChain 類之後，讓我們嘗試將天氣預報示例編碼為Python Markov Chain工作原理的表示。

資源

閱讀： Python 中的運算符

使用轉移矩陣參數化馬爾可夫鏈

在上一節中，Python 代碼使用包含所有可能狀態轉換的概率值的字典來參數化馬爾可夫鏈。 表示轉移概率的另一種方法是使用轉移矩陣，它是馬爾可夫鏈的標準、緊湊和表格表示。

在有數百種狀態的情況下，使用轉換矩陣比字典實現更有效。 馬爾可夫鏈類被修改如下，以接受一個轉移矩陣：

字典實現在狀態名稱上循環。 但是，在轉移矩陣的情況下，可以使用 NumPy 索引獲得 next_state 方法中的概率值：

資源

結論

馬爾可夫鍊是一種重要的數學工具，有助於簡化對複雜隨機過程未來狀態的預測； 它完全取決於過程的當前狀態，並將未來視為獨立於過去。 利用馬爾可夫屬性， Python 馬爾可夫鏈編碼是解決涉及復雜系統和動態變量的實際問題的有效方法。

無論是天氣預報、信用評級，還是在手機上打字預測，馬爾可夫鏈在各個學科都有牽強的應用。 根據參數的性質和應用，馬爾可夫鏈有不同的概念。 Python 馬爾可夫鍊是通過在 Python 中編碼來實現馬爾可夫鏈的一種合乎邏輯且有效的方式。

如果您想了解 Python、數據科學，請查看 IIIT-B 和 upGrad 的數據科學執行 PG 計劃，該計劃是為在職專業人士創建的，並提供 10 多個案例研究和項目、實用的實踐研討會、與行業專家的指導，與行業導師一對一，400 多個小時的學習和頂級公司的工作協助。