Python教程中的马尔可夫链

概述

你有没有想过专家气象学家如何准确预测天气或谷歌如何对不同的网页进行排名？ 他们如何在现实世界中制作迷人的 Python 应用程序。 这些计算很复杂，涉及多个动态变量，可以使用概率估计来解决。

这就是马尔可夫链的想法； 有个别状态（例如，天气状况），每个状态可以随机变为其他状态（下雨天可以变为晴天），这些变化或转换是基于概率的。 本文简要介绍了马尔可夫链的概念，以及如何利用Python 马尔可夫链在 Python 中编写马尔可夫链模型来解决实际问题。 如果您是初学者并且想获得数据科学方面的专业知识，请查看我们的数据科学课程。

内容概述

• 简单介绍一下马尔可夫链和马尔可夫性质的概念
• 马尔可夫链的数学和图形表达
• Python Markov Chain – 用 Python 编写 Markov Chain 示例

马尔可夫链简介

要使用Python 马尔可夫链解决实际问题，必须掌握马尔可夫链的概念。 1906 年，俄罗斯数学家安德烈·马尔科夫给出了马尔科夫链的定义——一个由随机变量组成的随机过程，这些变量从一个特定状态过渡到下一个特定状态，这些过渡基于特定的假设和概率规则。

称为马尔可夫属性的基本数学属性是随机变量转换的基础。 换句话说，马尔可夫链是一系列满足马尔可夫性质的变量 X1、X2、X3……。

马尔可夫链原理——马尔可夫性质

马尔可夫链基于马尔可夫属性。 离散时间马尔可夫特性理论指出，随机系统从一个特定状态变为下一个过渡状态的概率仅取决于当前状态和时间，与之前的状态无关。

随机过程的可能未来状态与之前存在的状态序列无关，这一事实使马尔可夫链成为仅依赖于变量当前状态的无记忆过程。

阅读： Python 中的内置数据结构

马尔可夫链的数学表达式

就概率分布而言，假设一个系统在时间实例“n”。 应用马尔可夫性质原理，下一个时间实例 n+1 的状态条件分布与系统在时间实例 1、2、…、n-1 的状态无关。

马尔可夫链的图形表示

有向图通常用于表示马尔可夫链。 在有向图中，节点表示随机变量的不同可能状态，而边表示系统在下一个时间实例中从一种状态移动到另一种状态的概率。 为了理解表示，让我们以预测天气为例。 假设随机变量是“天气”，它具有三种可能的状态，即。 天气 = {晴天、下雨、下雪}。 此场景的马尔可夫链可以表示为：

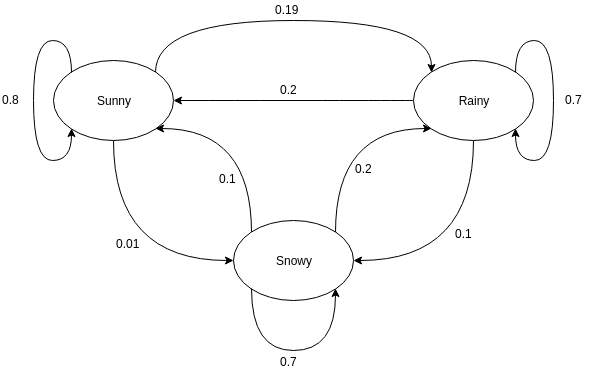
资源

在上面显示的图形表示中，假设随机变量的当前观察状态是晴天。 随机变量在下一次实例中取值为 Sunny 的概率为 0.8。 它也可以以 0.01 的概率取值 snowy，或以 0.19 的概率取值 rainy。 这里要注意的重要一点是，一个状态中存在的概率值总和总是为 1。

用 Python 编写马尔可夫链

为了更好地理解Python 马尔可夫链，让我们来看一个用 Python 编写马尔可夫链示例的实例。 在解决现实世界中的问题时，通常的做法是使用有效编码马尔可夫链的库。 然而，用 Python 编码马尔可夫链是开始马尔可夫链分析和模拟的绝佳方式。 因此出现了Python Markov Chain的实用程序。 让我们看看如何用 Python 编写上一节中给出的天气预报示例。 首先定义一个简单的类：

在定义了 MarkovChain 类之后，让我们尝试将天气预报示例编码为Python Markov Chain工作原理的表示。

资源

阅读： Python 中的运算符

使用转移矩阵参数化马尔可夫链

在上一节中，Python 代码使用包含所有可能状态转换的概率值的字典来参数化马尔可夫链。 表示转移概率的另一种方法是使用转移矩阵，它是马尔可夫链的标准、紧凑和表格表示。

在有数百种状态的情况下，使用转换矩阵比字典实现更有效。 马尔可夫链类被修改如下，以接受一个转移矩阵：

字典实现在状态名称上循环。 但是，在转移矩阵的情况下，可以使用 NumPy 索引获得 next_state 方法中的概率值：

资源

结论

马尔可夫链是一种重要的数学工具，有助于简化对复杂随机过程未来状态的预测； 它完全取决于过程的当前状态，并将未来视为独立于过去。 利用马尔可夫属性， Python 马尔可夫链编码是解决涉及复杂系统和动态变量的实际问题的有效方法。

无论是天气预报、信用评级，还是在手机上打字预测，马尔可夫链在各个学科都有牵强的应用。 根据参数的性质和应用，马尔可夫链有不同的概念。 Python 马尔可夫链是通过在 Python 中编码来实现马尔可夫链的一种合乎逻辑且有效的方式。

如果您想了解 Python、数据科学，请查看 IIIT-B 和 upGrad 的数据科学执行 PG 计划，该计划是为在职专业人士创建的，并提供 10 多个案例研究和项目、实用的实践研讨会、与行业专家的指导，与行业导师一对一，400 多个小时的学习和顶级公司的工作协助。