Python Tutorial의 마르코프 체인

개요

전문 기상학자가 날씨를 어떻게 정확하게 예측하는지 또는 Google이 다양한 웹페이지의 순위를 매기는지 생각해 본 적이 있습니까? 그들이 실제 세계에서 매혹적인 파이썬 애플리케이션을 만드는 방법. 이러한 계산은 복잡하고 동적이며 확률 추정을 사용하여 해결할 수 있는 여러 변수를 포함합니다.

여기에 Markov Chains의 아이디어가 있습니다. 각 상태가 무작위로 다른 상태로 변경될 수 있는 개별 상태(예: 기상 조건)가 있으며(비오는 날이 맑은 날로 변경될 수 있음) 이러한 변경 또는 전환은 확률 기반입니다. 이 기사에서는 Markov Chain의 개념과 Python Markov Chain 을 사용하여 Python에서 Markov Chain 모델을 코딩하여 실제 문제를 해결 하는 방법에 대해 간략하게 소개합니다 . 초보자이고 데이터 과학에 대한 전문 지식을 얻으려면 데이터 과학 과정을 확인하십시오.

콘텐츠 개요

• Markov Chain과 Markov Property의 개념에 대한 간략한 소개
• Markov Chain의 수학적 및 그래픽적 표현
• Python Markov Chain – Python으로 Markov Chain 예제 코딩

마르코프 체인 소개

Python Markov Chain 을 사용하여 실용적인 문제를 풀기 위해서는 Markov Chain의 개념을 이해하는 것이 필수적입니다. 1906년에 러시아 수학자 Andrei Markov는 Markov Chain의 정의를 제시했습니다. 이는 특정 상태에서 다음 상태로 전환하는 확률적 변수로 구성된 확률적 과정이며 이러한 전환은 특정 가정과 확률적 규칙을 기반으로 합니다.

마르코프 속성이라고 하는 기본적인 수학적 속성은 랜덤 변수의 전환의 기초입니다. 즉, Markov Chain은 Markov Property를 충족하는 일련의 변수 X1, X2, X3, …입니다.

마르코프 체인의 원리 – 마르코프 속성

마르코프 체인은 마르코프 속성을 기반으로 합니다. 이산 시간 마르코프 속성 이론은 임의의 시스템이 한 특정 상태에서 다음 전환 상태로 변경될 확률은 현재 상태와 시간에만 의존하고 이전 상태와는 무관하다고 말합니다.

무작위 프로세스의 가능한 미래 상태는 마르코프 체인을 변수의 현재 상태에만 의존하는 메모리 없는 프로세스로 만들기 전에 존재했던 상태 시퀀스와 무관하다는 사실입니다.

읽기: Python의 내장 데이터 구조

마르코프 사슬의 수학적 표현

확률 분포의 관점에서 시간 인스턴스 'n'에서 시스템을 가정합니다. Markov 속성의 원리를 적용하면 다음 시점 n+1에서의 상태의 조건부 분포는 시점 1, 2, …, n-1에서의 시스템 상태와 무관합니다.

Markov Chain의 그래픽 표현

방향 그래프는 종종 Markov Chain을 나타내는 데 사용됩니다. 유향 그래프에서 노드는 확률 변수의 서로 다른 가능한 상태를 나타내고 가장자리는 다음 시간 인스턴스에서 시스템이 한 상태에서 다른 상태로 이동할 확률을 나타냅니다. 표현을 이해하기 위해 날씨를 예측하는 예를 들어보겠습니다. 랜덤 변수가 '날씨'이고 세 가지 가능한 상태, 즉, 있다고 가정합니다. 날씨 = {맑음, 비, 눈}. 이 시나리오의 Markov Chain은 다음과 같이 나타낼 수 있습니다.

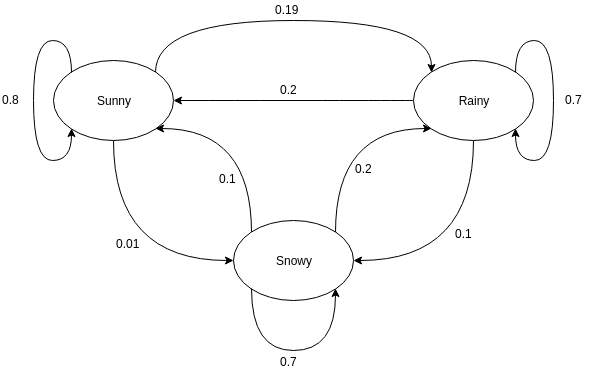
원천

위에 표시된 그래픽 표현에서 확률 변수의 현재 관찰된 상태가 밝다고 가정합니다. 다음 번 인스턴스에서 Sunny 값을 취할 확률 변수는 0.8입니다. 또한 0.01의 확률로 snowy 값을 취하거나 0.19의 확률로 비오는 값을 취할 수 있습니다. 여기서 주목해야 할 중요한 점은 상태에 존재하는 확률 값의 합은 항상 1이라는 것입니다.

파이썬에서 마르코프 체인 코딩하기

Python Markov Chain 을 더 잘 이해하기 위해 Markov Chain 의 예가 Python으로 코딩된 사례를 살펴보겠습니다. 현실 세계에서 문제를 해결하는 동안 Markov Chain을 효율적으로 인코딩하는 라이브러리를 사용하는 것이 일반적입니다. 그러나 Python에서 Markov Chain을 코딩하는 것은 Markov Chain 분석 및 시뮬레이션을 시작하는 훌륭한 방법입니다. 따라서 Python Markov Chain 의 유틸리티가 제공됩니다 . 이전 섹션에서 제공된 일기 예보의 예를 Python으로 코딩할 수 있는 방법을 살펴보겠습니다. 간단한 클래스를 정의하여 시작합니다.

MarkovChain 클래스를 정의했으므로 Python Markov Chain 이 작동 하는 방식을 나타내는 것으로 날씨 예측 예제를 코딩해 보겠습니다 .

원천

읽기: Python의 연산자

전환 행렬을 사용하여 마르코프 체인 매개변수화

이전 섹션에서 Python 코드는 가능한 모든 상태 전환의 확률 값이 포함된 사전을 사용하여 Markov Chain을 매개변수화했습니다. 전환 확률을 나타내는 다른 방법은 Markov Chain의 표준적이고 간결한 표 표현인 전환 행렬을 사용하는 것입니다.

수백 개의 상태가 있는 상황에서는 사전 구현보다 전환 매트릭스를 사용하는 것이 더 효율적입니다. Markov Chain 클래스는 전환 행렬을 허용하도록 다음과 같이 수정됩니다.

사전 구현은 상태 이름을 반복했습니다. 그러나 Transition Matrix의 경우 NumPy 인덱싱을 사용하여 next_state 메서드의 확률 값을 얻을 수 있습니다.

원천

결론

Markov Chains는 복잡한 확률적 프로세스의 미래 상태 예측을 단순화하는 데 도움이 되는 필수 수학적 도구입니다. 그것은 전적으로 프로세스의 현재 상태에 의존하고 미래를 과거와 무관한 것으로 봅니다. Markov 속성을 활용하는 Python Markov Chain 코딩은 복잡한 시스템 및 동적 변수와 관련된 실용적인 문제를 해결하는 효율적인 방법입니다.

날씨 예보, 신용 등급 또는 휴대 전화에서 단어 예측 입력 등 Markov Chains는 다양한 분야에서 광범위한 응용 프로그램을 제공합니다. 매개변수의 특성과 응용 프로그램에 따라 Markov Chain의 개념이 다릅니다. Python Markov Chain 은 Python으로 코딩하여 Markov Chain을 구현하는 논리적이고 효율적인 방법입니다.

python, 데이터 과학에 대해 자세히 알아보려면 작업 전문가를 위해 만들어졌으며 10개 이상의 사례 연구 및 프로젝트, 실용적인 실습 워크샵, 업계 전문가와의 멘토링을 제공하는 IIIT-B & upGrad의 데이터 과학 이그 제 큐 티브 PG 프로그램을 확인하십시오. , 업계 멘토와 1:1, 최고의 기업과 400시간 이상의 학습 및 취업 지원.