Python Eğitiminde Markov Zinciri
Yayınlanan: 2020-03-26İçindekiler
genel bakış
Uzman meteorologların hava durumu hakkında nasıl kesin bir tahminde bulunduğu veya Google'ın farklı web sayfalarını nasıl sıraladığı hiç aklınızdan geçti mi? Büyüleyici python uygulamalarını gerçek dünyada nasıl yapıyorlar. Bu hesaplamalar karmaşıktır ve dinamik olan ve olasılık tahminleri kullanılarak çözülebilen birkaç değişkeni içerir.
Markov Zincirleri fikri burada yatıyor; her bir durumun rastgele diğer durumlara dönüşebileceği (yağmurlu bir günün güneşli güne dönüşebileceği) bireysel durumlar (örneğin hava koşulları) vardır ve bu değişiklikler veya geçişler olasılık tabanlıdır. Bu makale, Markov Zincirleri kavramına ve gerçek dünya sorunlarını çözmek için Python'da Markov Zinciri modellerini kodlamak için Python Markov Zincirinin nasıl kullanılabileceğine kısa bir giriş sağlar. Yeni başlayan biriyseniz ve veri biliminde uzmanlık kazanmak istiyorsanız, veri bilimi kurslarımıza göz atın.
İçeriğe Genel Bakış
- Markov Zinciri ve Markov Mülkü kavramlarına kısa bir giriş
- Markov Zincirinin matematiksel ve grafiksel ifadesi
- Python Markov Zinciri – Python'da Markov Zinciri örneklerini kodlama
Markov Zincirine Giriş
Pratik problemleri çözmek için Python Markov Zincirini kullanmak için Markov Zincirleri kavramını anlamak esastır. 1906'da Rus matematikçi Andrei Markov, belirli bir durumdan diğerine geçiş yapan rastgele değişkenlerden oluşan stokastik bir süreç olan Markov Zinciri tanımını verdi ve bu geçişler belirli varsayımlara ve olasılık kurallarına dayanmaktadır.
Markov Özelliği adı verilen temel bir matematiksel özellik, rastgele değişkenlerin geçişlerinin temelidir. Başka bir deyişle, bir Markov Zinciri, Markov Özelliğini karşılayan bir dizi X1, X2, X3,….
Markov Zinciri Prensibi – Markov Özelliği
Bir Markov Zinciri, Markov Özelliğine dayanır. Ayrık zamanlı Markov Özelliği teorisi, rastgele bir sistemin belirli bir durumdan sonraki geçiş durumuna geçme olasılığının yalnızca mevcut duruma ve zamana bağlı olduğunu ve önceki durumlardan bağımsız olduğunu belirtir.
Rastgele bir sürecin olası gelecekteki durumunun, ondan önce var olan durum dizisinden bağımsız olması, Markov Zincirini yalnızca değişkenin mevcut durumuna bağlı olan hafızasız bir süreç haline getirir.
Okuyun: Python'da Yerleşik Veri Yapıları
Markov Zincirinin matematiksel ifadesi
Olasılık dağılımı açısından, 'n' anında bir sistem olduğunu varsayalım. Markov özelliği ilkesini uygulayarak, aşağıdaki zaman örneğindeki durumların koşullu dağılımı, n+1, sistemin 1, 2, …, n-1 anlarındaki durumlarından bağımsızdır.
Markov Zincirinin grafiksel gösterimi
Yönlendirilmiş grafikler genellikle bir Markov Zincirini temsil etmek için kullanılır. Yönlendirilmiş grafiklerde, düğümler rastgele değişkenlerin farklı olası durumlarını gösterirken, kenarlar sistemin bir sonraki zaman örneğinde bir durumdan diğerine geçme olasılığını gösterir. Temsili anlamak için hava durumunu tahmin etme örneğini ele alalım. Rastgele değişkenin 'hava durumu' olduğunu ve üç olası durumu olduğunu varsayalım. Hava durumu = {güneşli, yağmurlu, karlı}. Bu senaryo için Markov Zinciri şu şekilde temsil edilebilir:
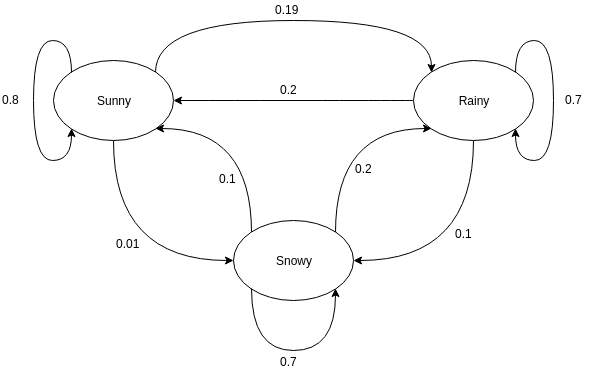
Kaynak
Yukarıda gösterilen grafik gösterimde, rastgele değişkenin mevcut gözlemlenen durumunun güneşli olduğunu söyleyin. Rastgele değişkenin bir sonraki zaman örneğinde güneşli değerini alma olasılığı 0,8'dir. Ayrıca 0,01 olasılıkla karlı veya 0,19 olasılıkla yağmurlu değerini alabilir. Burada dikkat edilmesi gereken önemli bir nokta, bir durumda bulunan olasılık değerlerinin her zaman 1'e eşit olacağıdır.
Python'da Markov Zinciri Kodlamak
Python Markov Zincirini daha iyi anlamak için , Python'da bir Markov Zinciri örneğinin kodlandığı bir örneği inceleyelim. Gerçek dünyadaki problemleri çözerken, Markov Zincirlerini verimli bir şekilde kodlayan bir kütüphane kullanmak yaygın bir uygulamadır. Ancak, Python'da Markov Zinciri kodlamak, Markov Zinciri analizi ve simülasyonuna başlamak için mükemmel bir yoldur. Dolayısıyla Python Markov Zincirinin faydası geliyor . Bir önceki bölümde verilen hava durumu tahmini örneğinin Python'da nasıl kodlanabileceğini görelim. Basit bir sınıf tanımlayarak başlayın:


MarkovChain sınıfını tanımladıktan sonra, Python Markov Zincirinin nasıl çalıştığının bir temsili olarak hava durumu tahmini örneğini kodlamayı deneyelim .

Kaynak
Okuyun: Python'da Operatörler
Geçiş Matrisi kullanılarak Markov Zincirlerinin Parametrelenmesi
Önceki bölümde, Python kodu, tüm olası durum geçişlerinin olasılık değerlerini içeren bir sözlük kullanarak Markov Zincirini parametrelendirdi. Geçiş olasılıklarını temsil etmenin alternatif bir yolu, bir Markov Zincirinin standart, kompakt ve tablo şeklinde bir temsili olan bir geçiş matrisi kullanmaktır.
Yüzlerce durumun olduğu durumlarda, Geçiş Matrisinin kullanımı bir sözlük uygulamasından daha verimlidir. Markov Zinciri sınıfı, bir geçiş matrisini kabul etmesi için aşağıdaki gibi değiştirilir:

Sözlük uygulaması eyalet adları üzerinde dönüyordu. Ancak, bir Geçiş Matrisi durumunda, next_state yöntemindeki olasılık değerleri, NumPy indeksleme kullanılarak elde edilebilir:

Kaynak
Çözüm
Markov Zincirleri, karmaşık stokastik süreçlerin gelecekteki durumunun tahminini basitleştirmeye yardımcı olan temel bir matematiksel araçtır; sadece sürecin mevcut durumuna bağlıdır ve geleceği geçmişten bağımsız olarak görür. Markov Özelliğini kullanan Python Markov Zinciri kodlaması, karmaşık sistemler ve dinamik değişkenler içeren pratik sorunları çözmenin etkili bir yoludur.
Cep telefonunuzda hava durumu tahmini, kredi notu veya yazarak kelime tahmini olsun, Markov Zincirleri çok çeşitli disiplinlerde çok yönlü uygulamalara sahiptir. Parametrelerin doğasına ve uygulamaya bağlı olarak, Markov Zincirlerinin farklı konseptleri vardır. Python Markov Zinciri , Markov Zincirlerini Python'da kodlayarak uygulamanın mantıklı ve verimli bir yoludur.
Python, veri bilimi hakkında bilgi edinmek istiyorsanız, IIIT-B & upGrad'ın çalışan profesyoneller için oluşturulan ve 10'dan fazla vaka çalışması ve proje, pratik uygulamalı atölye çalışmaları, endüstri uzmanlarıyla mentorluk sunan Veri Biliminde Yönetici PG Programına göz atın , sektör danışmanlarıyla bire bir, en iyi firmalarla 400+ saat öğrenim ve iş yardımı.
Markov geçiş matrisi nedir?
Birinden diğerine değişen belirli durumların olasılığı, bir kare matris olan bir geçiş matrisinde bulunur. Matris çarpımı yapmak, kalıpları belirlemek ve onu kullanarak tahminler yapmak için bir geçiş matrisi kullanabilirsiniz. Dinamik bir sistemde Markov geçiş matrisi, bir durumdan diğerine geçiş olasılığını tanımlayan kare bir matristir. Her satırda o satırın temsil ettiği durumdan diğer durumlara geçme olasılığı listelenir. Sonuç olarak, bir Markov geçiş matrisinin her satırı bire kadar ekler. Geçiş matrisleri, iki durum arasındaki geçişlerin nasıl üretildiğini açıklamak için kullanılır. Geçmişteki olayların bir sonucu olarak meydana gelme olasılığı az ya da çok olduğunda kullanılır.
Markov zincirinin emici durumu nedir?
Olasılık teorisine göre, bir soğurucu Markov zinciri, her durumun soğurucu bir duruma ulaşabileceği bir zincirdir. Emici bir durum, girdikten sonra çıkamayacağınız bir durumdur. Bir Markov zinciri, içinde en az bir soğurma durumu mevcutsa ve herhangi bir durumdan en az bir soğurma durumuna sınırlı sayıda adımda ulaşmak mümkünse, soğurduğu söylenir. Geçici bir durum, emici bir Markov zinciri tarafından emilmeyen bir durumdur.
Gizli Markov Modelleri (HMM) nedir?
HMM, incelenen sistemin gizli veya gözlemlenmemiş durumları olan bir Markov süreci olduğu matematiksel bir modeldir. Gizli Markov Modeli, makine öğrenimi ve jest tanıma ve konuşma tanıma gibi örüntü tanıma uygulamalarında kullanılır. Olasılık modelinde, Gizli Markov Modeli, görünen veya görünen olaylar ile gizli olaylar hakkında konuşmamıza izin verir. Ayrıca Doğal Dil İşleme (NLP) sorunları, Zaman Serileri ve daha pek çok gerçek dünya sorununun çözümüne de yardımcı olur. HMM'de iki temel varsayım yapılır. Mevcut gözlem ve gelecekteki durum tamamen mevcut duruma bağlıdır.
