Cadeia de Markov no Tutorial Python

Visão geral

Já passou pela sua cabeça como meteorologistas especialistas fazem uma previsão precisa do tempo ou como o Google classifica diferentes páginas da web? Como eles fazem os fascinantes aplicativos python no mundo real. Esses cálculos são complexos e envolvem diversas variáveis ​​que são dinâmicas e podem ser resolvidas usando estimativas de probabilidade.

Aqui reside a ideia das Cadeias de Markov; existem estados individuais (digamos, as condições climáticas) onde cada estado pode mudar aleatoriamente para outros estados (o dia chuvoso pode mudar para o dia ensolarado), e essas mudanças ou transições são baseadas em probabilidade. Este artigo fornece uma breve introdução ao conceito de Markov Chains e como Python Markov Chain pode ser utilizado para codificar modelos de Markov Chain em Python para resolver problemas do mundo real. Se você é iniciante e gostaria de ganhar experiência em ciência de dados, confira nossos cursos de ciência de dados.

Visão geral do conteúdo

• Uma breve introdução aos conceitos de Cadeia de Markov e Propriedade de Markov
• Expressão matemática e gráfica da Cadeia de Markov
• Python Markov Chain – codificação de exemplos de Markov Chain em Python

Introdução à Cadeia de Markov

Para usar o Python Markov Chain para resolver problemas práticos, é essencial entender o conceito de Markov Chains. Em 1906, o matemático russo Andrei Markov deu a definição de uma Cadeia de Markov – um processo estocástico que consiste em variáveis ​​aleatórias que transitam de um estado particular para outro, e essas transições são baseadas em suposições específicas e regras probabilísticas.

Uma propriedade matemática fundamental chamada Propriedade de Markov é a base das transições das variáveis ​​aleatórias. Em outras palavras, uma Cadeia de Markov é uma série de variáveis ​​X1, X2, X3,… que cumprem a Propriedade de Markov.

Princípio da Cadeia de Markov - Propriedade de Markov

Uma Cadeia de Markov é baseada na Propriedade de Markov. A teoria da propriedade de Markov em tempo discreto afirma que a probabilidade de um sistema aleatório mudar de um estado particular para o próximo estado de transição depende apenas do estado atual e do tempo e é independente dos estados anteriores.

O fato de o provável estado futuro de um processo aleatório ser independente da sequência de estados que existiam antes dele torna a Cadeia de Markov um processo sem memória que depende apenas do estado atual da variável.

Leia: Construído em estruturas de dados em Python

A expressão matemática da Cadeia de Markov

Em termos de distribuição de probabilidade, suponha um sistema na instância de tempo 'n.' Aplicando o princípio da propriedade de Markov, a distribuição condicional dos estados na instância de tempo seguinte, n+1, é independente dos estados do sistema nas instâncias de tempo 1, 2, …, n-1.

Representação gráfica da Cadeia de Markov

Gráficos direcionados são frequentemente usados ​​para representar uma Cadeia de Markov. Nos grafos direcionados, os nós indicam diferentes estados prováveis ​​das variáveis ​​aleatórias enquanto as arestas denotam a probabilidade do sistema passar de um estado para outro na próxima instância de tempo. Para entender a representação, tomemos o exemplo da previsão do tempo. Suponha que a variável aleatória seja 'tempo' e tenha três estados possíveis, viz. Tempo = {ensolarado, chuvoso, com neve}. A Cadeia de Markov para este cenário pode ser representada como:

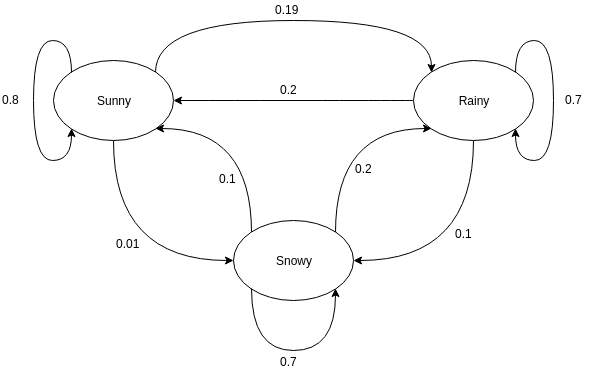
Fonte

Na representação gráfica mostrada acima, digamos que o estado atual observado da variável aleatória seja ensolarado. A probabilidade da variável aleatória assumir o valor ensolarado na próxima instância de tempo é 0,8. Também pode assumir o valor nevado com probabilidade de 0,01, ou chuvoso com probabilidade de 0,19. Uma coisa importante a notar aqui é que os valores de probabilidade existentes em um estado sempre somarão 1.

Codificando uma Cadeia de Markov em Python

Para entender melhor Python Markov Chain , vamos passar por uma instância em que um exemplo de Markov Chain é codificado em Python. Ao resolver problemas no mundo real, é prática comum usar uma biblioteca que codifique Cadeias de Markov de forma eficiente. No entanto, codificar Markov Chain em Python é uma excelente maneira de começar na análise e simulação de Markov Chain. Daí vem a utilidade do Python Markov Chain . Vamos ver como o exemplo de previsão do tempo dado na seção anterior pode ser codificado em Python. Comece definindo uma classe simples:

Tendo definido a classe MarkovChain, vamos tentar codificar o exemplo de previsão do tempo como uma representação de como Python Markov Chain funciona.

Fonte

Leia: Operadores em Python

Parametrizando Cadeias de Markov usando Matriz de Transição

Na seção anterior, o código Python parametrizou a Cadeia de Markov usando um dicionário que continha os valores de probabilidade de todas as transições de estado prováveis. Uma forma alternativa de representar as probabilidades de transição é usando uma matriz de transição, que é uma representação padrão, compacta e tabular de uma Cadeia de Markov.

Em situações onde existem centenas de estados, o uso da Matriz de Transição é mais eficiente do que uma implementação de dicionário. A classe Markov Chain é modificada da seguinte forma para aceitar uma matriz de transição:

A implementação do dicionário estava fazendo um loop sobre os nomes dos estados. No entanto, no caso de uma Matriz de Transição, os valores de probabilidade no método next_state podem ser obtidos usando a indexação NumPy:

Fonte

Conclusão

As Cadeias de Markov são uma ferramenta matemática essencial que ajuda a simplificar a previsão do estado futuro de processos estocásticos complexos; depende unicamente do estado atual do processo e vê o futuro como independente do passado. Utilizando a Propriedade Markov, a codificação Python Markov Chain é uma maneira eficiente de resolver problemas práticos que envolvem sistemas complexos e variáveis ​​dinâmicas.

Seja previsão do tempo, classificação de crédito ou previsão de palavras no seu celular, as Markov Chains têm aplicativos rebuscados em uma ampla variedade de disciplinas. Dependendo da natureza dos parâmetros e da aplicação, existem diferentes conceitos de Cadeias de Markov. Python Markov Chain é uma maneira lógica e eficiente de implementar Markov Chains codificando-as em Python.

Se você está curioso para aprender sobre python, ciência de dados, confira o Programa PG Executivo em Ciência de Dados do IIIT-B & upGrad, criado para profissionais que trabalham e oferece mais de 10 estudos de caso e projetos, workshops práticos práticos, orientação com especialistas do setor , 1-on-1 com mentores do setor, mais de 400 horas de aprendizado e assistência de trabalho com as principais empresas.