Lanțul Markov în Tutorial Python

Prezentare generală

V-a trecut vreodată prin minte modul în care meteorologii experți fac o predicție precisă a vremii sau cum clasifică Google diferite pagini web? Cum creează aplicațiile fascinante Python în lumea reală. Aceste calcule sunt complexe și implică mai multe variabile care sunt dinamice și pot fi rezolvate folosind estimări de probabilitate.

Aici se află ideea Lanțurilor Markov; există stări individuale (să zicem, condițiile meteorologice) în care fiecare stare se poate schimba aleatoriu în alte stări (ziua ploioasă se poate schimba în ziua însorită), iar aceste schimbări sau tranziții sunt bazate pe probabilitate. Acest articol oferă o scurtă introducere a conceptului de lanțuri Markov și a modului în care Python Markov Chain poate fi utilizat pentru a codifica modele Markov Chain în Python pentru a rezolva probleme din lumea reală. Dacă sunteți începător și doriți să obțineți experiență în știința datelor, consultați cursurile noastre de știință a datelor.

Prezentare generală a conținutului

• O scurtă introducere în conceptele de lanț Markov și proprietate Markov
• Exprimarea matematică și grafică a lanțului Markov
• Python Markov Chain – exemple de codificare Markov Chain în Python

Introducere în lanțul Markov

Pentru a utiliza Python Markov Chain pentru rezolvarea problemelor practice, este esențial să înțelegem conceptul de Markov Chains. În 1906, matematicianul rus Andrei Markov a dat definiția unui lanț Markov – un proces stocastic constând din variabile aleatorii care trec de la o anumită stare la alta, iar aceste tranziții se bazează pe presupuneri specifice și reguli probabilistice.

O proprietate matematică fundamentală numită proprietatea Markov stă la baza tranzițiilor variabilelor aleatoare. Cu alte cuvinte, un lanț Markov este o serie de variabile X1, X2, X3,... care îndeplinesc Proprietatea Markov.

Principiul lanțului Markov – proprietatea Markov

Un lanț Markov se bazează pe proprietatea Markov. Teoria proprietății Markov în timp discret afirmă că probabilitatea ca un sistem aleatoriu să treacă de la o anumită stare la următoarea stare de tranziție depinde doar de starea și timpul prezent și este independentă de stările precedente.

Faptul că starea viitoare probabilă a unui proces aleatoriu este independentă de succesiunea de stări care a existat înainte de a face lanțul Markov un proces fără memorie care depinde doar de starea curentă a variabilei.

Citiți: Structuri de date încorporate în Python

Expresia matematică a Lanțului Markov

În ceea ce privește o distribuție de probabilitate, presupunem un sistem la instanta de timp „n”. Aplicând principiul proprietății Markov, distribuția condiționată a stărilor la următoarea instanță de timp, n+1, este independentă de stările sistemului la instanțele de timp 1, 2, …, n-1.

Reprezentarea grafică a lanțului Markov

Graficele direcționate sunt adesea folosite pentru a reprezenta un lanț Markov. În graficele direcționate, nodurile indică diferite stări probabile ale variabilelor aleatoare, în timp ce marginile denotă probabilitatea ca sistemul să treacă de la o stare la alta în următoarea instanță de timp. Pentru a înțelege reprezentarea, să luăm exemplul de a prezice vremea. Să presupunem că variabila aleatoare este „vremea” și are trei stări posibile, adică. Vremea = {soare, ploaie, zăpadă}. Lanțul Markov pentru acest scenariu poate fi reprezentat ca:

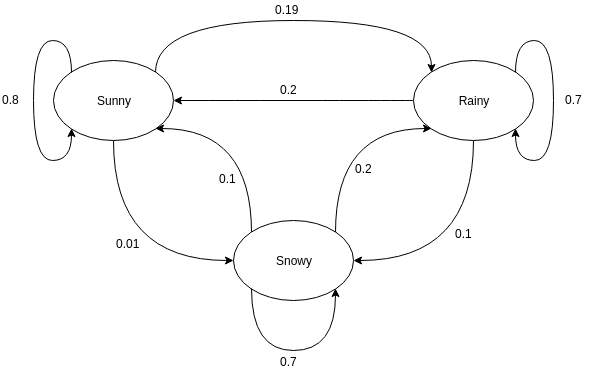
Sursă

În reprezentarea grafică prezentată mai sus, să spunem că starea curentă observată a variabilei aleatoare este însorită. Probabilitatea ca variabila aleatoare să ia valoarea sunny la următoarea instanță este 0,8. De asemenea, poate lua valoarea ninsoare cu o probabilitate de 0,01 sau ploios cu o probabilitate de 0,19. Un lucru important de remarcat aici este că valorile probabilității existente într-o stare se vor însuma întotdeauna până la 1.

Codarea unui lanț Markov în Python

Pentru a înțelege mai bine Python Markov Chain , să trecem printr-un exemplu în care un exemplu de Markov Chain este codificat în Python. În timpul rezolvării problemelor din lumea reală, este o practică obișnuită să folosiți o bibliotecă care codifică eficient lanțurile Markov. Cu toate acestea, codificarea lanțului Markov în Python este o modalitate excelentă de a începe analiza și simularea lanțului Markov. De aici vine utilitatea lanțului Python Markov . Să vedem cum exemplul de predicție a vremii dat în secțiunea anterioară poate fi codificat în Python. Începeți prin a defini o clasă simplă:

După ce am definit clasa MarkovChain, să încercăm să codificăm exemplul de predicție a vremii ca o reprezentare a modului în care funcționează Python Markov Chain .

Sursă

Citiți: Operatori în Python

Parametrizarea lanțurilor Markov folosind matricea de tranziție

În secțiunea anterioară, codul Python a parametrizat Lanțul Markov folosind un dicționar care conținea valorile probabilității tuturor tranzițiilor de stare probabile. O modalitate alternativă de reprezentare a probabilităților de tranziție este utilizarea unei matrice de tranziție, care este o reprezentare standard, compactă și tabelară a unui lanț Markov.

În situațiile în care există sute de state, utilizarea Matricei de tranziție este mai eficientă decât o implementare a dicționarului. Clasa Markov Chain este modificată după cum urmează pentru a accepta o matrice de tranziție:

Implementarea dicționarului trecea în buclă peste numele statelor. Cu toate acestea, în cazul unei matrice de tranziție, valorile probabilității din metoda next_state pot fi obținute folosind indexarea NumPy:

Sursă

Concluzie

Lanțurile Markov sunt un instrument matematic esențial care ajută la simplificarea predicției stării viitoare a proceselor stocastice complexe; depinde numai de starea actuală a procesului și vede viitorul ca independent de trecut. Folosind proprietatea Markov, codarea Python Markov Chain este o modalitate eficientă de a rezolva probleme practice care implică sisteme complexe și variabile dinamice.

Fie că este vorba despre prognoza meteo, evaluarea creditului sau predicția cuvintelor introduse pe telefonul mobil, Markov Chains are aplicații exagerate într-o mare varietate de discipline. În funcție de natura parametrilor și de aplicație, există diferite concepte de lanțuri Markov. Python Markov Chain este o modalitate logică și eficientă de a implementa Markov Chains prin codificarea lor în Python.

Dacă sunteți curios să aflați despre python, știința datelor, consultați programul Executive PG în știința datelor de la IIIT-B și upGrad, care este creat pentru profesioniști care lucrează și oferă peste 10 studii de caz și proiecte, ateliere practice practice, mentorat cu experți din industrie , 1-la-1 cu mentori din industrie, peste 400 de ore de învățare și asistență profesională cu firme de top.