Pythonチュートリアルのマルコフ連鎖

概要

専門の気象学者が天気を正確に予測する方法や、Googleがさまざまなウェブページをランク付けする方法に頭を悩ませたことはありませんか？ 彼らが現実の世界で魅力的なPythonアプリケーションをどのように作成するか。 これらの計算は複雑であり、動的であり、確率推定を使用して解くことができるいくつかの変数が含まれます。

ここにマルコフ連鎖の考え方があります。 各州がランダムに他の州に変化する可能性がある（たとえば、気象条件）個々の州があり（雨の日は晴れの日に変化する可能性があります）、これらの変化または遷移は確率に基づいています。 この記事では、マルコフ連鎖の概念と、 Pythonマルコフ連鎖を利用してPythonでマルコフ連鎖モデルをコーディングして実際の問題を解決する方法について簡単に紹介します。 初心者でデータサイエンスの専門知識を習得したい場合は、データサイエンスコースをご覧ください。

コンテンツの概要

• マルコフ連鎖とマルコフ性の概念の簡単な紹介
• マルコフ連鎖の数学的およびグラフィカルな表現
• Pythonマルコフ連鎖–Pythonでのマルコフ連鎖の例のコーディング

マルコフ連鎖入門

Pythonマルコフ連鎖を使用して実際の問題を解決するには、マルコフ連鎖の概念を理解することが不可欠です。 1906年、ロシアの数学者アンドレイマルコフは、マルコフ連鎖の定義を示しました。これは、ある特定の状態から次の状態に遷移する確率変数で構成される確率過程であり、これらの遷移は特定の仮定と確率規則に基づいています。

マルコフ性と呼ばれる基本的な数学的特性は、確率変数の遷移の基礎です。 言い換えれば、マルコフ連鎖は、マルコフ性を満たす一連の変数X1、X2、X3、…です。

マルコフ連鎖の原理–マルコフ性

マルコフ連鎖はマルコフ性に基づいています。 離散時間マルコフ性の理論は、ランダムシステムが特定の状態から次の遷移状態に変化する確率は、現在の状態と時間にのみ依存し、前の状態とは無関係であると述べています。

ランダムプロセスの予想される将来の状態が、マルコフ連鎖を変数の現在の状態のみに依存するメモリのないプロセスにする前に存在していた状態のシーケンスとは無関係であるという事実。

読む： Pythonの組み込みデータ構造

マルコフ連鎖の数式

確率分布の観点から、時間インスタンス'n'のシステムを想定します。 マルコフ性の原理を適用すると、次の時間インスタンスn + 1での状態の条件付き分布は、時間インスタンス1、2、…、n-1でのシステムの状態とは無関係です。

マルコフ連鎖のグラフィック表現

有向グラフは、マルコフ連鎖を表すためによく使用されます。 有向グラフでは、ノードは確率変数のさまざまな可能性のある状態を示し、エッジは次の時間インスタンスでシステムが1つの状態から別の状態に移動する確率を示します。 表現を理解するために、天気を予測する例を見てみましょう。 確率変数が「天気」であり、3つの可能な状態があると仮定します。 天気={晴れ、雨、雪}。 このシナリオのマルコフ連鎖は、次のように表すことができます。

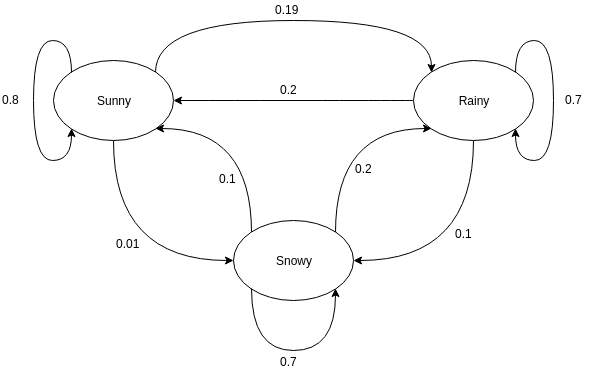
ソース

上に示したグラフ表示で、確率変数の現在の観測状態が晴れているとします。 確率変数が次回のインスタンスで晴れの値をとる確率は0.8です。 また、0.01の確率で雪の値を取得することも、0.19の確率で雨の値を取得することもできます。 ここで注意すべき重要なことは、状態に存在する確率値の合計は常に1になるということです。

Pythonでのマルコフ連鎖のコーディング

Pythonマルコフ連鎖をよりよく理解するために、マルコフ連鎖の例がPythonでコーディングされている例を見てみましょう。 現実の世界で問題を解決する一方で、マルコフ連鎖を効率的にエンコードするライブラリを使用するのが一般的な方法です。 ただし、Pythonでマルコフ連鎖をコーディングすることは、マルコフ連鎖の分析とシミュレーションを開始するための優れた方法です。 したがって、 Pythonマルコフ連鎖のユーティリティが登場します。 前のセクションで示した天気予報の例をPythonでコーディングする方法を見てみましょう。 単純なクラスを定義することから始めます。

マルコフ連鎖クラスを定義したら、 Pythonマルコフ連鎖がどのように機能するかを表すものとして天気予報の例をコーディングしてみましょう。

ソース

読む： Pythonの演算子

遷移行列を使用したマルコフ連鎖のパラメーター化

前のセクションでは、Pythonコードは、すべての可能性のある状態遷移の確率値を含む辞書を使用して、マルコフ連鎖をパラメーター化しました。 遷移確率を表す別の方法は、マルコフ連鎖の標準的でコンパクトな表形式の表現である遷移行列を使用することです。

数百の状態がある状況では、遷移行列の使用は辞書の実装よりも効率的です。 マルコフ連鎖クラスは、遷移行列を受け入れるように次のように変更されます。

辞書の実装は、州の名前をループしていました。 ただし、遷移行列の場合、next_stateメソッドの確率値は、NumPyインデックスを使用して取得できます。

ソース

結論

マルコフ連鎖は、複雑な確率過程の将来の状態の予測を単純化するのに役立つ重要な数学的ツールです。 それは単にプロセスの現在の状態に依存し、未来を過去から独立していると見なします。 マルコフ性を利用するPythonマルコフ連鎖コーディングは、複雑なシステムや動的変数を含む実際的な問題を解決するための効率的な方法です。

天気予報、信用格付け、携帯電話での単語予測の入力など、マルコフ連鎖はさまざまな分野で幅広い用途を持っています。 パラメータの性質とアプリケーションに応じて、マルコフ連鎖の概念は異なります。 Pythonマルコフ連鎖は、Pythonでコーディングすることにより、マルコフ連鎖を実装するための論理的かつ効率的な方法です。

python、データサイエンスについて知りたい場合は、IIIT-BとupGradのデータサイエンスのエグゼクティブPGプログラムをご覧ください。これは、働く専門家向けに作成され、10以上のケーススタディとプロジェクト、実践的なハンズオンワークショップ、業界の専門家とのメンターシップを提供します。 、業界のメンターと1対1で、400時間以上の学習とトップ企業との仕事の支援。