Chaîne de Markov dans le didacticiel Python

Aperçu

Avez-vous déjà pensé à la façon dont les météorologues experts font une prévision précise du temps ou à la façon dont Google classe différentes pages Web ? Comment ils font les applications python fascinantes dans le monde réel. Ces calculs sont complexes et impliquent plusieurs variables qui sont dynamiques et peuvent être résolues à l'aide d'estimations de probabilité.

C'est là que réside l'idée des chaînes de Markov ; il existe des états individuels (par exemple, les conditions météorologiques) où chaque état peut se transformer de manière aléatoire en d'autres états (le jour de pluie peut se transformer en jour ensoleillé), et ces changements ou transitions sont basés sur la probabilité. Cet article donne une brève introduction au concept de chaînes de Markov et explique comment Python Markov Chain peut être utilisé pour coder des modèles de chaînes de Markov en Python afin de résoudre des problèmes du monde réel. Si vous êtes débutant et souhaitez acquérir une expertise en science des données, consultez nos cours de science des données.

Aperçu du contenu

• Une brève introduction aux concepts de chaîne de Markov et de propriété de Markov
• Expression mathématique et graphique de la chaîne de Markov
• Chaîne de Markov Python - codage d'exemples de chaîne de Markov en Python

Introduction à la chaîne de Markov

Pour utiliser Python Markov Chain pour résoudre des problèmes pratiques, il est essentiel de comprendre le concept de Markov Chains. En 1906, le mathématicien russe Andrei Markov a donné la définition d'une chaîne de Markov - un processus stochastique composé de variables aléatoires qui passent d'un état particulier à l'autre, et ces transitions sont basées sur des hypothèses spécifiques et des règles probabilistes.

Une propriété mathématique fondamentale appelée la propriété de Markov est à la base des transitions des variables aléatoires. En d'autres termes, une chaîne de Markov est une série de variables X1, X2, X3,… qui remplissent la propriété de Markov.

Principe de la chaîne de Markov – Propriété de Markov

Une chaîne de Markov est basée sur la propriété de Markov. La théorie de la propriété de Markov à temps discret stipule que la probabilité qu'un système aléatoire passe d'un état particulier à l'état de transition suivant ne dépend que de l'état et du temps actuels et est indépendante des états précédents.

Le fait que l'état futur probable d'un processus aléatoire soit indépendant de la séquence d'états qui existaient avant lui fait de la chaîne de Markov un processus sans mémoire qui ne dépend que de l'état actuel de la variable.

Lire : Structures de données intégrées en Python

L'expression mathématique de la chaîne de Markov

En termes de distribution de probabilité, supposons un système à l'instance temporelle « n ». En appliquant le principe de la propriété de Markov, la distribution conditionnelle des états à l'instance temporelle suivante, n+1, est indépendante des états du système aux instances temporelles 1, 2, …, n-1.

Représentation graphique de la chaîne de Markov

Les graphes orientés sont souvent utilisés pour représenter une chaîne de Markov. Dans les graphes orientés, les nœuds indiquent différents états probables des variables aléatoires tandis que les arêtes indiquent la probabilité que le système passe d'un état à un autre lors de la prochaine instance. Pour comprendre la représentation, prenons l'exemple de la prévision du temps. Supposons que la variable aléatoire est "météo" et qu'elle a trois états possibles, à savoir. Météo = {ensoleillé, pluvieux, neigeux}. La chaîne de Markov pour ce scénario peut être représentée comme suit :

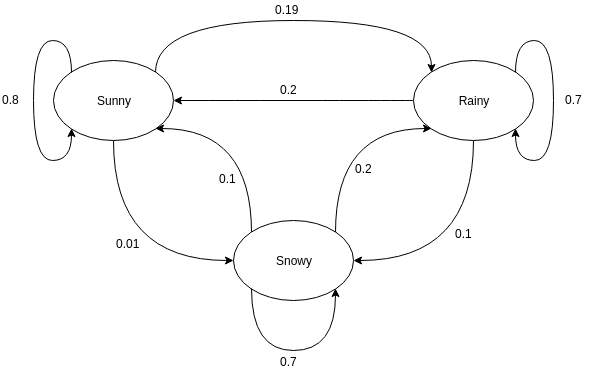
La source

Dans la représentation graphique ci-dessus, supposons que l'état actuel observé de la variable aléatoire est ensoleillé. La probabilité que la variable aléatoire prenne la valeur ensoleillé à la prochaine instance est de 0,8. Il peut aussi prendre la valeur neigeux avec une probabilité de 0,01, ou pluvieux avec une probabilité de 0,19. Une chose importante à noter ici est que les valeurs de probabilité existant dans un état totaliseront toujours 1.

Coder une chaîne de Markov en Python

Pour mieux comprendre Python Markov Chain , passons en revue une instance où un exemple de Markov Chain est codé en Python. Lors de la résolution de problèmes dans le monde réel, il est courant d'utiliser une bibliothèque qui encode efficacement les chaînes de Markov. Cependant, coder la chaîne de Markov en Python est un excellent moyen de se lancer dans l'analyse et la simulation de la chaîne de Markov. D'où l'utilité de Python Markov Chain . Voyons comment l'exemple de prévision météorologique donné dans la section précédente peut être codé en Python. Commencez par définir une classe simple :

Après avoir défini la classe MarkovChain, essayons de coder l'exemple de prévision météorologique comme une représentation du fonctionnement de Python Markov Chain .

La source

Lire : Opérateurs en Python

Paramétrage des chaînes de Markov à l'aide de la matrice de transition

Dans la section précédente, le code Python a paramétré la chaîne de Markov à l'aide d'un dictionnaire contenant les valeurs de probabilité de toutes les transitions d'état probables. Une autre façon de représenter les probabilités de transition consiste à utiliser une matrice de transition, qui est une représentation standard, compacte et tabulaire d'une chaîne de Markov.

Dans les situations où il y a des centaines d'états, l'utilisation de la matrice de transition est plus efficace qu'une implémentation de dictionnaire. La classe Chaîne de Markov est modifiée comme suit pour qu'elle accepte une matrice de transition :

L'implémentation du dictionnaire faisait une boucle sur les noms d'états. Cependant, dans le cas d'une matrice de transition, les valeurs de probabilité dans la méthode next_state peuvent être obtenues en utilisant l'indexation NumPy :

La source

Conclusion

Les chaînes de Markov sont un outil mathématique essentiel qui aide à simplifier la prédiction de l'état futur des processus stochastiques complexes ; il dépend uniquement de l'état actuel du processus et considère l'avenir comme indépendant du passé. En utilisant la propriété de Markov, le codage Python Markov Chain est un moyen efficace de résoudre des problèmes pratiques impliquant des systèmes complexes et des variables dynamiques.

Qu'il s'agisse de prévisions météorologiques, de notation de crédit ou de prédiction de mots sur votre téléphone mobile, les chaînes de Markov ont des applications farfelues dans une grande variété de disciplines. Selon la nature des paramètres et l'application, il existe différents concepts de chaînes de Markov. Python Markov Chain est un moyen logique et efficace d'implémenter des chaînes de Markov en les codant en Python.

Si vous êtes curieux d'en savoir plus sur Python, la science des données, consultez le programme Executive PG en science des données de IIIT-B & upGrad qui est créé pour les professionnels en activité et propose plus de 10 études de cas et projets, des ateliers pratiques, du mentorat avec des experts de l'industrie. , 1-on-1 avec des mentors de l'industrie, plus de 400 heures d'apprentissage et d'aide à l'emploi avec les meilleures entreprises.