Markov-Kette im Python-Tutorial

Überblick

Ist Ihnen schon einmal in den Sinn gekommen, wie erfahrene Meteorologen das Wetter genau vorhersagen oder wie Google verschiedene Webseiten bewertet? Wie sie die faszinierenden Python-Anwendungen in der realen Welt machen. Diese Berechnungen sind komplex und umfassen mehrere dynamische Variablen, die mithilfe von Wahrscheinlichkeitsschätzungen gelöst werden können.

Hier liegt die Idee der Markov-Ketten; Es gibt einzelne Zustände (z. B. die Wetterbedingungen), in denen jeder Zustand zufällig in andere Zustände wechseln kann (ein Regentag kann in einen sonnigen Tag übergehen), und diese Änderungen oder Übergänge basieren auf Wahrscheinlichkeiten. Dieser Artikel gibt eine kurze Einführung in das Konzept von Markov Chains und wie Python Markov Chain verwendet werden kann, um Markov Chain-Modelle in Python zu codieren, um reale Probleme zu lösen. Wenn Sie Anfänger sind und sich Fachwissen in Data Science aneignen möchten, sehen Sie sich unsere Data Science-Kurse an.

Inhaltsübersicht

• Eine kurze Einführung in die Konzepte der Markov-Kette und der Markov-Eigenschaft
• Mathematischer und grafischer Ausdruck der Markov-Kette
• Python-Markov-Kette – Codierung von Beispielen für Markov-Ketten in Python

Einführung in die Markov-Kette

Um die Python-Markov-Kette zur Lösung praktischer Probleme zu verwenden, ist es wichtig, das Konzept der Markov-Ketten zu verstehen. 1906 definierte der russische Mathematiker Andrei Markov eine Markov-Kette – einen stochastischen Prozess, der aus Zufallsvariablen besteht, die von einem bestimmten Zustand in den nächsten übergehen, und diese Übergänge basieren auf bestimmten Annahmen und Wahrscheinlichkeitsregeln.

Eine grundlegende mathematische Eigenschaft namens Markov-Eigenschaft ist die Grundlage für die Übergänge der Zufallsvariablen. Mit anderen Worten, eine Markov-Kette ist eine Reihe von Variablen X1, X2, X3, … die die Markov-Eigenschaft erfüllen.

Prinzip der Markov-Kette – Markov-Eigenschaft

Eine Markov-Kette basiert auf der Markov-Eigenschaft. Die Theorie der zeitdiskreten Markov-Eigenschaft besagt, dass die Wahrscheinlichkeit, dass ein zufälliges System von einem bestimmten Zustand in den nächsten Übergangszustand wechselt, nur vom gegenwärtigen Zustand und der Zeit abhängt und unabhängig von den vorhergehenden Zuständen ist.

Die Tatsache, dass der wahrscheinliche zukünftige Zustand eines zufälligen Prozesses unabhängig von der Folge von Zuständen ist, die davor existierten, macht die Markov-Kette zu einem gedächtnislosen Prozess, der nur vom aktuellen Zustand der Variablen abhängt.

Lesen Sie: Eingebaute Datenstrukturen in Python

Der mathematische Ausdruck der Markov-Kette

Nehmen Sie in Bezug auf eine Wahrscheinlichkeitsverteilung ein System zum Zeitpunkt 'n' an. Unter Anwendung des Prinzips der Markov-Eigenschaft ist die bedingte Verteilung der Zustände zum folgenden Zeitpunkt n+1 unabhängig von den Zuständen des Systems zu den Zeitpunkten 1, 2, …, n-1.

Grafische Darstellung der Markov-Kette

Gerichtete Graphen werden oft verwendet, um eine Markov-Kette darzustellen. In den gerichteten Graphen geben die Knoten unterschiedliche wahrscheinliche Zustände der Zufallsvariablen an, während die Kanten die Wahrscheinlichkeit angeben, dass sich das System im nächsten Zeitpunkt von einem Zustand in einen anderen bewegt. Um die Darstellung zu verstehen, nehmen wir das Beispiel der Vorhersage des Wetters. Angenommen, die Zufallsvariable ist "Wetter" und hat drei mögliche Zustände, nämlich. Wetter = {sonnig, regnerisch, verschneit}. Die Markov-Kette für dieses Szenario kann wie folgt dargestellt werden:

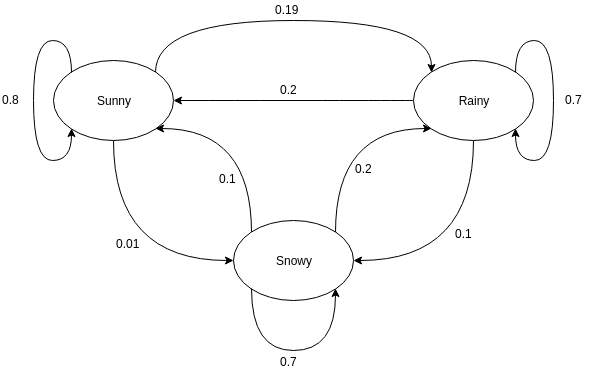
Quelle

Nehmen wir in der oben gezeigten grafischen Darstellung an, dass der aktuell beobachtete Zustand der Zufallsvariablen sonnig ist. Die Wahrscheinlichkeit, dass die Zufallsvariable zum nächsten Zeitpunkt den Wert sonnig annimmt, beträgt 0,8. Es kann auch den Wert verschneit mit einer Wahrscheinlichkeit von 0,01 oder regnerisch mit einer Wahrscheinlichkeit von 0,19 annehmen. Wichtig dabei ist, dass sich die in einem Zustand vorhandenen Wahrscheinlichkeitswerte immer zu 1 summieren.

Codieren einer Markov-Kette in Python

Um Python Markov Chain besser zu verstehen , lassen Sie uns einen Fall durchgehen, in dem ein Beispiel für Markov Chain in Python codiert ist. Beim Lösen von Problemen in der realen Welt ist es üblich, eine Bibliothek zu verwenden, die Markov-Ketten effizient codiert. Das Codieren von Markov-Ketten in Python ist jedoch eine hervorragende Möglichkeit, um mit der Analyse und Simulation von Markov-Ketten zu beginnen. Daher kommt die Nützlichkeit von Python Markov Chain . Sehen wir uns an, wie das Beispiel der Wettervorhersage aus dem vorherigen Abschnitt in Python codiert werden kann. Beginnen Sie mit der Definition einer einfachen Klasse:

Nachdem wir die MarkovChain-Klasse definiert haben, versuchen wir, das Wettervorhersagebeispiel als Darstellung der Funktionsweise von Python Markov Chain zu codieren .

Quelle

Lesen Sie: Operatoren in Python

Parametrieren von Markov-Ketten mit Übergangsmatrix

Im vorherigen Abschnitt parametrisierte der Python-Code die Markov-Kette mithilfe eines Wörterbuchs, das die Wahrscheinlichkeitswerte aller wahrscheinlichen Zustandsübergänge enthielt. Eine alternative Möglichkeit zur Darstellung der Übergangswahrscheinlichkeiten ist die Verwendung einer Übergangsmatrix, die eine standardmäßige, kompakte und tabellarische Darstellung einer Markov-Kette ist.

In Situationen, in denen es Hunderte von Zuständen gibt, ist die Verwendung der Übergangsmatrix effizienter als eine Wörterbuchimplementierung. Die Markov Chain-Klasse wird wie folgt modifiziert, damit sie eine Übergangsmatrix akzeptiert:

Die Dictionary-Implementierung durchlief die Zustandsnamen. Im Fall einer Übergangsmatrix können die Wahrscheinlichkeitswerte in der Methode next_state jedoch mithilfe der NumPy-Indizierung abgerufen werden:

Quelle

Fazit

Markov-Ketten sind ein wesentliches mathematisches Werkzeug, das hilft, die Vorhersage des zukünftigen Zustands komplexer stochastischer Prozesse zu vereinfachen; sie hängt allein vom aktuellen Stand des Prozesses ab und betrachtet die Zukunft als unabhängig von der Vergangenheit. Unter Verwendung der Markov-Eigenschaft ist die Python-Markov-Kettencodierung eine effiziente Möglichkeit, praktische Probleme zu lösen, die komplexe Systeme und dynamische Variablen betreffen.

Ob Wettervorhersage, Bonitätsbewertung oder Wortvorhersage auf Ihrem Mobiltelefon, Markov-Ketten haben weit hergeholte Anwendungen in einer Vielzahl von Disziplinen. Abhängig von der Art der Parameter und der Anwendung gibt es unterschiedliche Konzepte von Markov-Ketten. Die Python-Markov-Kette ist eine logische und effiziente Möglichkeit, Markov-Ketten zu implementieren, indem sie in Python codiert werden.

Wenn Sie mehr über Python und Data Science erfahren möchten, besuchen Sie das Executive PG Program in Data Science von IIIT-B & upGrad, das für Berufstätige entwickelt wurde und mehr als 10 Fallstudien und Projekte, praktische Workshops und Mentoring mit Branchenexperten bietet , 1-on-1 mit Mentoren aus der Branche, über 400 Stunden Lern- und Jobunterstützung bei Top-Unternehmen.