Tutorial de cadenas de Markov en Python

Visión de conjunto

¿Alguna vez te ha pasado por la cabeza cómo expertos meteorólogos hacen una predicción precisa del tiempo o cómo Google clasifica diferentes páginas web? Cómo hacen las fascinantes aplicaciones de Python en el mundo real. Estos cálculos son complejos e involucran varias variables que son dinámicas y pueden resolverse mediante estimaciones de probabilidad.

Aquí radica la idea de las Cadenas de Markov; hay estados individuales (digamos, las condiciones climáticas) donde cada estado puede cambiar aleatoriamente a otros estados (un día lluvioso puede cambiar a un día soleado), y estos cambios o transiciones se basan en la probabilidad. Este artículo ofrece una breve introducción al concepto de cadenas de Markov y cómo se puede utilizar Python Markov Chain para codificar modelos de cadenas de Markov en Python para resolver problemas del mundo real. Si es un principiante y le gustaría adquirir experiencia en ciencia de datos, consulte nuestros cursos de ciencia de datos.

Descripción general del contenido

• Una breve introducción a los conceptos de Cadena de Markov y Propiedad de Markov
• Expresión matemática y gráfica de la Cadena de Markov
• Python Markov Chain : codificación de ejemplos de cadenas de Markov en Python

Introducción a la Cadena de Markov

Para usar Python Markov Chain para resolver problemas prácticos, es esencial comprender el concepto de Markov Chains. En 1906, el matemático ruso Andrei Markov dio la definición de Cadena de Markov: un proceso estocástico que consta de variables aleatorias que pasan de un estado particular al siguiente, y estas transiciones se basan en suposiciones específicas y reglas probabilísticas.

Una propiedad matemática fundamental llamada Propiedad de Markov es la base de las transiciones de las variables aleatorias. En otras palabras, una Cadena de Markov es una serie de variables X1, X2, X3,… que cumplen la Propiedad de Markov.

Principio de la Cadena de Markov – Propiedad de Markov

Una cadena de Markov se basa en la propiedad de Markov. La teoría de la propiedad de Markov en tiempo discreto establece que la probabilidad de que un sistema aleatorio cambie de un estado particular al siguiente estado de transición depende solo del estado y el tiempo presentes y es independiente de los estados precedentes.

El hecho de que el estado futuro probable de un proceso aleatorio sea independiente de la secuencia de estados que existieron antes hace que la Cadena de Markov sea un proceso sin memoria que depende únicamente del estado actual de la variable.

Leer: Estructuras de datos integradas en Python

La expresión matemática de la Cadena de Markov

En términos de una distribución de probabilidad, suponga un sistema en la instancia de tiempo 'n'. Aplicando el principio de la propiedad de Markov, la distribución condicional de los estados en el siguiente instante de tiempo, n+1, es independiente de los estados del sistema en los instantes de tiempo 1, 2,…, n-1.

Representación gráfica de la Cadena de Markov

Los gráficos dirigidos se utilizan a menudo para representar una cadena de Markov. En los gráficos dirigidos, los nodos indican diferentes estados probables de las variables aleatorias, mientras que los bordes denotan la probabilidad de que el sistema se mueva de un estado a otro en la siguiente instancia de tiempo. Para entender la representación, tomemos el ejemplo de predecir el clima. Suponga que la variable aleatoria es 'clima' y tiene tres estados posibles, a saber. Clima = {soleado, lluvioso, nevado}. La Cadena de Markov para este escenario se puede representar como:

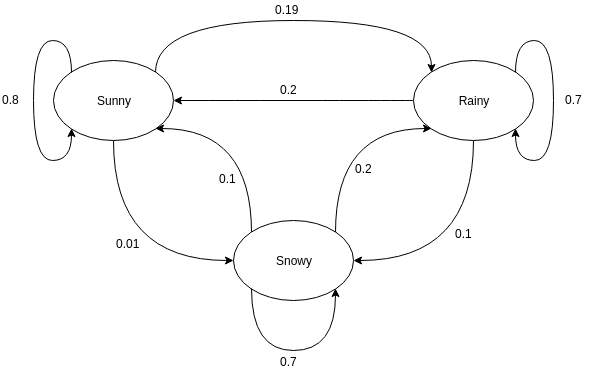
Fuente

En la representación gráfica que se muestra arriba, digamos que el estado observado actual de la variable aleatoria es soleado. La probabilidad de que la variable aleatoria tome el valor soleado en la siguiente instancia de tiempo es 0.8. También puede tomar el valor nevado con una probabilidad de 0,01, o lluvioso con una probabilidad de 0,19. Una cosa importante a tener en cuenta aquí es que los valores de probabilidad existentes en un estado siempre sumarán 1.

Codificando una cadena de Markov en Python

Para comprender mejor la Cadena de Markov de Python , veamos una instancia en la que se codifica un ejemplo de Cadena de Markov en Python. Mientras se resuelven problemas en el mundo real, es una práctica común usar una biblioteca que codifique cadenas de Markov de manera eficiente. Sin embargo, la codificación de la Cadena de Markov en Python es una excelente manera de comenzar con el análisis y la simulación de la Cadena de Markov. De ahí viene la utilidad de Python Markov Chain . Veamos cómo se puede codificar en Python el ejemplo de predicción del tiempo dado en la sección anterior. Comience definiendo una clase simple:

Habiendo definido la clase MarkovChain, intentemos codificar el ejemplo de predicción meteorológica como una representación de cómo funciona Python Markov Chain .

Fuente

Leer: Operadores en Python

Parametrización de cadenas de Markov utilizando la matriz de transición

En la sección anterior, el código de Python parametrizó la Cadena de Markov utilizando un diccionario que contenía los valores de probabilidad de todas las transiciones de estado probables. Una forma alternativa de representar las probabilidades de transición es usar una matriz de transición, que es una representación estándar, compacta y tabular de una cadena de Markov.

En situaciones donde hay cientos de estados, el uso de Transition Matrix es más eficiente que la implementación de un diccionario. La clase Cadena de Markov se modifica de la siguiente manera para que acepte una matriz de transición:

La implementación del diccionario estaba recorriendo los nombres de los estados. Sin embargo, en el caso de una Matriz de transición, los valores de probabilidad en el método next_state se pueden obtener utilizando la indexación NumPy:

Fuente

Conclusión

Las Cadenas de Markov son una herramienta matemática esencial que ayuda a simplificar la predicción del estado futuro de procesos estocásticos complejos; depende únicamente del estado actual del proceso y ve el futuro como independiente del pasado. Utilizando la propiedad de Markov, la codificación de Python Markov Chain es una forma eficiente de resolver problemas prácticos que involucran sistemas complejos y variables dinámicas.

Ya sea el pronóstico del tiempo, la calificación crediticia o la predicción de palabras en su teléfono móvil, las cadenas de Markov tienen aplicaciones inverosímiles en una amplia variedad de disciplinas. Dependiendo de la naturaleza de los parámetros y la aplicación, existen diferentes conceptos de Cadenas de Markov. Python Markov Chain es una forma lógica y eficiente de implementar cadenas de Markov codificándolas en Python.

Si tiene curiosidad por aprender sobre python, ciencia de datos, consulte el Programa PG ejecutivo en ciencia de datos de IIIT-B y upGrad, que se creó para profesionales que trabajan y ofrece más de 10 estudios de casos y proyectos, talleres prácticos prácticos, tutoría con expertos de la industria. , 1 a 1 con mentores de la industria, más de 400 horas de aprendizaje y asistencia laboral con las mejores empresas.