Łańcuch Markowa w samouczku Pythona

Przegląd

Czy kiedykolwiek przyszło Ci do głowy, jak eksperci meteorolodzy dokonują precyzyjnej prognozy pogody lub jak Google klasyfikuje różne strony internetowe? Jak tworzą fascynujące aplikacje Pythona w prawdziwym świecie. Obliczenia te są złożone i obejmują kilka zmiennych, które są dynamiczne i można je rozwiązać za pomocą oszacowań prawdopodobieństwa.

Tu leży idea Łańcuchów Markowa; istnieją indywidualne stany (powiedzmy warunki pogodowe), w których każdy stan może losowo zmienić się w inny (dzień deszczowy może zmienić się w dzień słoneczny), a te zmiany lub przejścia są oparte na prawdopodobieństwie. Ten artykuł zawiera krótkie wprowadzenie do koncepcji łańcuchów Markowa i sposobu wykorzystania łańcucha Markowa w języku Python do kodowania modeli łańcuchów Markowa w Pythonie w celu rozwiązywania rzeczywistych problemów. Jeśli jesteś początkującym i chciałbyś zdobyć doświadczenie w nauce o danych, zapoznaj się z naszymi kursami z nauk o danych.

Przegląd treści

• Krótkie wprowadzenie do pojęć Markowa Łańcucha i Markov Property
• Matematyczny i graficzny wyraz łańcucha Markowa
• Python Markov Chain – kodowanie przykładów łańcucha Markowa w Pythonie

Wprowadzenie do łańcucha Markowa

Aby używać łańcucha Markowa w Pythonie do rozwiązywania praktycznych problemów, konieczne jest zrozumienie koncepcji łańcuchów Markowa. W 1906 r. rosyjski matematyk Andriej Markow podał definicję łańcucha Markowa – procesu stochastycznego składającego się ze zmiennych losowych, które przechodzą z jednego stanu do drugiego, a przejścia te opierają się na określonych założeniach i regułach probabilistycznych.

Podstawowa właściwość matematyczna zwana Własnością Markowa jest podstawą przejść zmiennych losowych. Innymi słowy, łańcuch Markowa to seria zmiennych X1, X2, X3,…, które spełniają Własność Markowa.

Zasada łańcucha Markowa – Własność Markowa

Łańcuch Markowa opiera się na Nieruchomości Markowa. Teoria własności Markowa w czasie dyskretnym mówi, że prawdopodobieństwo przejścia systemu losowego z jednego określonego stanu do następnego stanu przejściowego zależy tylko od stanu obecnego i czasu i jest niezależne od stanów poprzedzających.

Fakt, że prawdopodobny przyszły stan procesu losowego jest niezależny od sekwencji stanów, które istniały przed nim, sprawia, że ​​Łańcuch Markowa jest procesem pozbawionym pamięci i zależnym tylko od aktualnego stanu zmiennej.

Przeczytaj: Wbudowane struktury danych w Pythonie

Matematyczne wyrażenie łańcucha Markowa

Jeśli chodzi o rozkład prawdopodobieństwa, załóżmy system w instancji czasowej 'n'. Stosując zasadę własności Markowa, warunkowy rozkład stanów w kolejnych instancjach czasowych, n+1, jest niezależny od stanów układu w instancjach czasowych 1, 2, …, n-1.

Graficzna reprezentacja łańcucha Markowa

Wykresy ukierunkowane są często używane do reprezentowania łańcucha Markowa. W grafach skierowanych węzły wskazują różne prawdopodobne stany zmiennych losowych, podczas gdy krawędzie oznaczają prawdopodobieństwo przejścia układu z jednego stanu do drugiego w następnej instancji czasu. Aby zrozumieć reprezentację, weźmy przykład przewidywania pogody. Załóżmy, że zmienna losowa to „pogoda” i ma trzy możliwe stany, a mianowicie. Pogoda = {słonecznie, deszczowo, śnieżnie}. Łańcuch Markowa dla tego scenariusza można przedstawić jako:

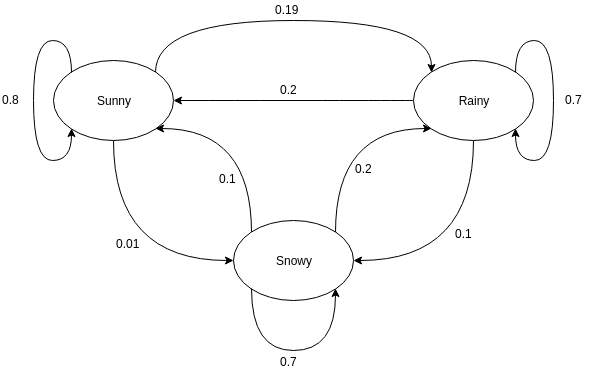
Źródło

W przedstawionej powyżej reprezentacji graficznej powiedzmy, że bieżący obserwowany stan zmiennej losowej jest słoneczny. Prawdopodobieństwo, że zmienna losowa przyjmie wartość sunny w następnym wystąpieniu wynosi 0,8. Może również przyjąć wartość śnieżną z prawdopodobieństwem 0,01 lub deszczową z prawdopodobieństwem 0,19. Ważną rzeczą, na którą należy zwrócić uwagę, jest to, że wartości prawdopodobieństwa występujące w stanie zawsze sumują się do 1.

Kodowanie łańcucha Markowa w Pythonie

Aby lepiej zrozumieć Python Markov Chain , przejdźmy przez instancję, w której przykład Markowa Chain jest zakodowany w Pythonie. Podczas rozwiązywania problemów w świecie rzeczywistym powszechną praktyką jest korzystanie z biblioteki, która efektywnie koduje łańcuchy Markowa. Jednak kodowanie łańcucha Markowa w Pythonie to doskonały sposób na rozpoczęcie analizy i symulacji łańcucha Markowa. Stąd pojawia się użyteczność Pythona Markowa Chain . Zobaczmy, jak przykład prognozowania pogody podany w poprzedniej sekcji można zakodować w Pythonie. Zacznij od zdefiniowania prostej klasy:

Po zdefiniowaniu klasy MarkovChain spróbujmy zakodować przykład przewidywania pogody jako reprezentację działania łańcucha Markowa w Pythonie .

Źródło

Przeczytaj: Operatory w Pythonie

Parametryzacja łańcuchów Markowa za pomocą macierzy przejścia

W poprzedniej sekcji kod Pythona sparametryzował łańcuch Markowa przy użyciu słownika, który zawierał wartości prawdopodobieństwa wszystkich prawdopodobnych zmian stanu. Alternatywnym sposobem przedstawienia prawdopodobieństw przejścia jest użycie macierzy przejścia, która jest standardową, zwartą i tabelaryczną reprezentacją łańcucha Markowa.

W sytuacjach, w których istnieją setki stanów, użycie macierzy przejścia jest bardziej wydajne niż implementacja słownikowa. Klasa Markov Chain została zmodyfikowana w następujący sposób, aby akceptowała macierz przejścia:

Implementacja słownika zapętlała się po nazwach stanów. Jednak w przypadku Transition Matrix wartości prawdopodobieństwa w metodzie next_state można uzyskać za pomocą indeksowania NumPy:

Źródło

Wniosek

Łańcuchy Markowa są niezbędnym narzędziem matematycznym, które pomaga uprościć przewidywanie przyszłego stanu złożonych procesów stochastycznych; zależy wyłącznie od aktualnego stanu procesu i postrzega przyszłość jako niezależną od przeszłości. Wykorzystując właściwość Markowa, kodowanie łańcuchowe Markowa w Pythonie jest skutecznym sposobem rozwiązywania praktycznych problemów, które dotyczą złożonych systemów i zmiennych dynamicznych.

Niezależnie od tego, czy chodzi o prognozowanie pogody, ocenę kredytową, czy wpisywanie przewidywań słów na telefonie komórkowym, Markov Chains ma daleko idące zastosowania w wielu różnych dyscyplinach. W zależności od charakteru parametrów i zastosowania istnieją różne koncepcje łańcuchów Markowa. Łańcuch Markowa w Pythonie to logiczny i wydajny sposób implementacji łańcuchów Markowa poprzez zakodowanie ich w Pythonie.

Jeśli chcesz dowiedzieć się więcej o Pythonie, nauce o danych, sprawdź program Executive PG w dziedzinie Data Science IIIT-B i upGrad, który jest stworzony dla pracujących profesjonalistów i oferuje ponad 10 studiów przypadków i projektów, praktyczne warsztaty praktyczne, mentoring z ekspertami z branży , 1 na 1 z mentorami branżowymi, ponad 400 godzin nauki i pomocy w pracy z najlepszymi firmami.