سلسلة ماركوف في دروس بايثون

ملخص

هل خطر ببالك يومًا كيف يقوم خبراء الأرصاد الجوية بتوقع دقيق للطقس أو كيف تصنف Google صفحات الويب المختلفة؟ كيف يصنعون تطبيقات بيثون الرائعة في العالم الحقيقي. هذه الحسابات معقدة وتتضمن العديد من المتغيرات الديناميكية ويمكن حلها باستخدام تقديرات الاحتمالات.

هنا تكمن فكرة سلاسل ماركوف. هناك حالات فردية (على سبيل المثال ، الأحوال الجوية) حيث يمكن لكل حالة أن تتغير بشكل عشوائي إلى حالات أخرى (يمكن أن يتغير يوم ممطر إلى يوم مشمس) ، وهذه التغييرات أو التحولات تعتمد على الاحتمالات. تقدم هذه المقالة مقدمة موجزة لمفهوم سلاسل ماركوف وكيف يمكن استخدام سلسلة بايثون ماركوف لترميز نماذج ماركوف تشين في بايثون لحل مشكلات العالم الحقيقي . إذا كنت مبتدئًا وترغب في اكتساب الخبرة في علم البيانات ، فراجع دورات علوم البيانات لدينا.

نظرة عامة على المحتوى

• مقدمة موجزة عن مفاهيم سلسلة ماركوف وممتلكات ماركوف
• تعبير رياضي ورسمي لسلسلة ماركوف
• سلسلة Python Markov - ترميز أمثلة Markov Chain في Python

مقدمة لسلسلة ماركوف

لاستخدام Python Markov Chain لحل المشكلات العملية ، من الضروري فهم مفهوم سلاسل Markov. في عام 1906 ، قدم عالم الرياضيات الروسي أندريه ماركوف تعريفًا لسلسلة ماركوف - وهي عملية عشوائية تتكون من متغيرات عشوائية تنتقل من حالة معينة إلى أخرى ، وتستند هذه التحولات إلى افتراضات محددة وقواعد احتمالية.

خاصية رياضية أساسية تسمى خاصية ماركوف هي أساس انتقالات المتغيرات العشوائية. بمعنى آخر ، سلسلة ماركوف هي سلسلة من المتغيرات X1 ، X2 ، X3 ، ... التي تحقق خاصية ماركوف.

مبدأ سلسلة ماركوف - ملكية ماركوف

تعتمد سلسلة ماركوف على خاصية ماركوف. تنص نظرية خاصية ماركوف للوقت المنفصل على أن احتمال تغيير نظام عشوائي من حالة معينة إلى حالة الانتقال التالية يعتمد فقط على الحالة والوقت الحاليين ومستقل عن الحالات السابقة.

حقيقة أن الحالة المستقبلية المحتملة لعملية عشوائية مستقلة عن تسلسل الحالات التي كانت موجودة قبل أن تجعل سلسلة ماركوف عملية لا تحتوي على ذاكرة تعتمد فقط على الحالة الحالية للمتغير.

قراءة: هياكل البيانات المضمنة في Python

التعبير الرياضي لسلسلة ماركوف

من حيث التوزيع الاحتمالي ، افترض وجود نظام في وقت مثيل "n". تطبيق مبدأ خاصية ماركوف ، التوزيع الشرطي للحالات في المثال الزمني التالي ، n + 1 ، مستقل عن حالات النظام في الحالات الزمنية 1 ، 2 ، ... ، n-1.

تمثيل رسومي لسلسلة ماركوف

غالبًا ما تُستخدم الرسوم البيانية الموجهة لتمثيل سلسلة ماركوف. في الرسوم البيانية الموجهة ، تشير العقد إلى حالات مختلفة محتملة للمتغيرات العشوائية بينما تشير الحواف إلى احتمال انتقال النظام من حالة إلى أخرى في المرة التالية. لفهم التمثيل ، دعونا نأخذ مثال التنبؤ بالطقس. افترض أن المتغير العشوائي هو "الطقس" ، وله ثلاث حالات محتملة. الطقس = {مشمس ، ممطر ، ثلجي}. يمكن تمثيل سلسلة ماركوف لهذا السيناريو على النحو التالي:

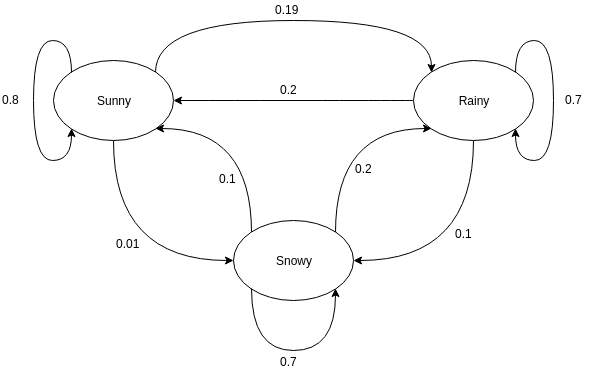
مصدر

في التمثيل الرسومي الموضح أعلاه ، لنفترض أن الحالة الحالية الملاحظة للمتغير العشوائي مشمسة. احتمال أن يأخذ المتغير العشوائي القيمة مشمسًا في المرة التالية هو 0.8. يمكن أن تأخذ أيضًا القيمة ثلجي مع احتمال 0.01 ، أو مطر مع احتمال 0.19. الشيء المهم الذي يجب ملاحظته هنا هو أن قيم الاحتمال الموجودة في حالة ما ستصل دائمًا إلى 1.

ترميز سلسلة ماركوف في بايثون

لفهم Python Markov Chain بشكل أفضل ، دعنا ننتقل إلى مثال حيث تم ترميز مثال لسلسلة Markov في Python. أثناء حل المشكلات في العالم الحقيقي ، من الشائع استخدام مكتبة تقوم بترميز سلاسل ماركوف بكفاءة. ومع ذلك ، يعد ترميز Markov Chain في Python طريقة ممتازة للبدء في تحليل ومحاكاة Markov Chain. ومن هنا تأتي فائدة سلسلة بايثون ماركوف . دعونا نرى كيف يمكن ترميز مثال التنبؤ بالطقس الوارد في القسم السابق في Python. ابدأ بتحديد فئة بسيطة:

بعد تحديد فئة MarkovChain ، دعونا نحاول ترميز مثال التنبؤ بالطقس كتمثيل لكيفية عمل Python Markov Chain .

مصدر

قراءة: عوامل التشغيل في Python

معلمة سلاسل ماركوف باستخدام مصفوفة الانتقال

في القسم السابق ، حددت شفرة Python معلمات سلسلة Markov باستخدام قاموس يحتوي على قيم الاحتمالات لجميع انتقالات الحالة المحتملة. هناك طريقة بديلة لتمثيل احتمالات الانتقال وهي استخدام مصفوفة انتقالية ، وهي تمثيل معياري ومضغوط وجدولي لسلسلة ماركوف.

في المواقف التي توجد فيها مئات الحالات ، يكون استخدام مصفوفة الانتقال أكثر كفاءة من تنفيذ القاموس. يتم تعديل فئة Markov Chain على النحو التالي لقبول مصفوفة الانتقال:

تم تنفيذ القاموس بشكل متكرر فوق أسماء الحالات. ومع ذلك ، في حالة وجود مصفوفة انتقالية ، يمكن الحصول على قيم الاحتمالية في طريقة next_state باستخدام فهرسة NumPy:

مصدر

خاتمة

سلاسل ماركوف هي أداة رياضية أساسية تساعد على تبسيط التنبؤ بالحالة المستقبلية للعمليات العشوائية المعقدة ؛ يعتمد فقط على الحالة الحالية للعملية وينظر إلى المستقبل على أنه مستقل عن الماضي. باستخدام خاصية Markov ، يعد تشفير Python Markov Chain طريقة فعالة لحل المشكلات العملية التي تتضمن أنظمة معقدة ومتغيرات ديناميكية.

سواء كان ذلك للتنبؤ بالطقس أو التصنيف الائتماني أو كتابة التنبؤ بالكلمات على هاتفك المحمول ، فإن Markov Chains لديها تطبيقات بعيدة الاحتمال في مجموعة متنوعة من التخصصات. اعتمادًا على طبيعة المعلمات والتطبيق ، هناك مفاهيم مختلفة لسلاسل ماركوف. سلسلة Python Markov هي طريقة منطقية وفعالة لتنفيذ سلاسل Markov عن طريق ترميزها في Python.

إذا كنت مهتمًا بمعرفة المزيد عن Python وعلوم البيانات ، فراجع برنامج IIIT-B & upGrad's Executive PG في علوم البيانات والذي تم إنشاؤه للمهنيين العاملين ويقدم أكثر من 10 دراسات حالة ومشاريع ، وورش عمل عملية عملية ، وإرشاد مع خبراء الصناعة ، وجهاً لوجه مع موجهين في الصناعة ، وأكثر من 400 ساعة من التعلم والمساعدة في العمل مع الشركات الكبرى.