Цепь Маркова в Python Tutorial

Обзор

Вам когда-нибудь приходило в голову, как опытные метеорологи делают точные прогнозы погоды или как Google ранжирует различные веб-страницы? Как они делают увлекательные приложения на Python в реальном мире. Эти расчеты сложны и включают несколько переменных, которые являются динамическими и могут быть решены с использованием оценок вероятности.

В этом заключается идея цепей Маркова; существуют отдельные состояния (скажем, погодные условия), где каждое состояние может случайным образом меняться в другие состояния (дождливый день может смениться солнечным днем), и эти изменения или переходы основаны на вероятности. В этой статье дается краткое введение в концепцию цепей Маркова и то, как цепь Маркова Python можно использовать для кодирования моделей цепей Маркова в Python для решения реальных задач. Если вы новичок и хотите получить опыт в науке о данных, ознакомьтесь с нашими курсами по науке о данных.

Обзор контента

• Краткое введение в концепции цепи Маркова и свойства Маркова
• Математическое и графическое выражение цепи Маркова
• Python Markov Chain — кодирование примеров цепей Маркова на Python

Введение в цепь Маркова

Чтобы использовать цепь Маркова Python для решения практических задач, важно понять концепцию цепей Маркова. В 1906 году русский математик Андрей Марков дал определение цепи Маркова — стохастического процесса, состоящего из случайных величин, которые переходят из одного конкретного состояния в другое, и эти переходы основаны на определенных предположениях и вероятностных правилах.

Фундаментальное математическое свойство, называемое свойством Маркова, лежит в основе переходов случайных величин. Другими словами, цепь Маркова — это ряд переменных X1, X2, X3,…, которые удовлетворяют свойству Маркова.

Принцип цепи Маркова - свойство Маркова

Цепь Маркова основана на свойстве Маркова. Теория марковского свойства дискретного времени утверждает, что вероятность перехода случайной системы из одного конкретного состояния в следующее переходное состояние зависит только от текущего состояния и времени и не зависит от предыдущих состояний.

Тот факт, что вероятное будущее состояние случайного процесса не зависит от последовательности состояний, существовавших до него, делает цепь Маркова процессом без памяти, который зависит только от текущего состояния переменной.

Читайте: Встроенные структуры данных в Python

Математическое выражение цепи Маркова

С точки зрения распределения вероятностей, предположим, что система находится в момент времени 'n'. Применяя принцип марковского свойства, условное распределение состояний в следующий момент времени n+1 не зависит от состояний системы в моменты времени 1, 2, …, n-1.

Графическое представление цепи Маркова

Ориентированные графы часто используются для представления цепи Маркова. На ориентированных графах узлы обозначают различные вероятные состояния случайных величин, а ребра обозначают вероятность перехода системы из одного состояния в другое в следующий момент времени. Чтобы понять представление, давайте возьмем пример предсказания погоды. Предположим, что случайной величиной является «погода», и она имеет три возможных состояния, а именно. Погода = {солнечно, дождливо, снежно}. Цепь Маркова для этого сценария может быть представлена ​​как:

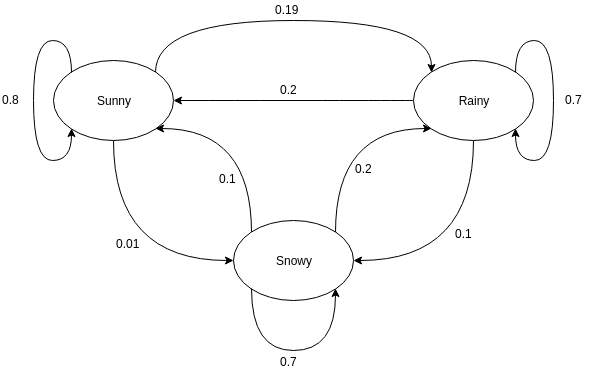
Источник

В графическом представлении, показанном выше, предположим, что текущее наблюдаемое состояние случайной величины солнечное. Вероятность того, что случайная величина примет значение солнечно в следующий момент времени, равна 0,8. Он также может принимать значение «снег» с вероятностью 0,01 или «дождь» с вероятностью 0,19. Здесь важно отметить, что значения вероятности, существующие в состоянии, всегда будут в сумме равны 1.

Кодирование цепи Маркова в Python

Чтобы лучше понять цепь Маркова Python , давайте рассмотрим пример, в котором пример цепи Маркова закодирован на Python. При решении задач в реальном мире обычной практикой является использование библиотеки, которая эффективно кодирует цепи Маркова. Тем не менее, кодирование цепей Маркова на Python — отличный способ начать анализ и моделирование цепей Маркова. Отсюда и полезность Python Markov Chain . Давайте посмотрим, как пример предсказания погоды, приведенный в предыдущем разделе, можно закодировать на Python. Начните с определения простого класса:

Определив класс MarkovChain, давайте попробуем закодировать пример прогноза погоды как представление того, как работает цепь Маркова Python .

Источник

Читайте: Операторы в Python

Параметризация цепей Маркова с использованием матрицы переходов

В предыдущем разделе код Python параметризовал цепь Маркова, используя словарь, который содержал значения вероятности всех вероятных переходов состояний. Альтернативным способом представления вероятностей перехода является использование матрицы перехода, которая представляет собой стандартное, компактное и табличное представление цепи Маркова.

В ситуациях, когда есть сотни состояний, использование матрицы перехода более эффективно, чем реализация словаря. Класс цепи Маркова изменен следующим образом, чтобы он мог принимать матрицу перехода:

Реализация словаря зацикливалась на именах состояний. Однако в случае матрицы перехода значения вероятности в методе next_state можно получить с помощью индексации NumPy:

Источник

Заключение

Цепи Маркова — важный математический инструмент, помогающий упростить предсказание будущего состояния сложных случайных процессов; оно зависит исключительно от текущего состояния процесса и рассматривает будущее как независимое от прошлого. Используя свойство Маркова, кодирование цепочки Маркова Python — это эффективный способ решения практических задач, связанных со сложными системами и динамическими переменными.

Будь то прогноз погоды, кредитный рейтинг или предсказание слов на мобильном телефоне, цепи Маркова найдут применение в самых разных областях. В зависимости от характера параметров и применения существуют разные концепции цепей Маркова. Цепь Маркова Python — это логичный и эффективный способ реализации цепей Маркова путем их кодирования на Python.

Если вам интересно узнать о python и науке о данных, ознакомьтесь с программой Executive PG IIIT-B и upGrad по науке о данных , которая создана для работающих профессионалов и предлагает более 10 тематических исследований и проектов, практические практические семинары, наставничество с отраслевыми экспертами. , общение один на один с отраслевыми наставниками, более 400 часов обучения и помощь в трудоустройстве в ведущих фирмах.