Rantai Markov dalam Tutorial Python

Diterbitkan: 2020-03-26

Daftar isi

Ringkasan

Pernahkah terlintas dalam pikiran Anda bagaimana ahli meteorologi membuat prediksi cuaca yang tepat atau bagaimana Google memberi peringkat pada halaman web yang berbeda? Bagaimana mereka membuat aplikasi python yang menarik di dunia nyata. Perhitungan ini kompleks dan melibatkan beberapa variabel yang dinamis dan dapat diselesaikan dengan menggunakan perkiraan probabilitas.

Di sinilah letak ide Rantai Markov; ada negara bagian (misalnya, kondisi cuaca) di mana setiap negara bagian dapat secara acak berubah menjadi negara bagian lain (hari hujan dapat berubah menjadi hari yang cerah), dan perubahan atau transisi ini berbasis probabilitas. Artikel ini memberikan pengenalan singkat tentang konsep Rantai Markov dan bagaimana Rantai Markov Python dapat digunakan untuk mengkode model Rantai Markov dengan Python untuk memecahkan masalah dunia nyata. Jika Anda seorang pemula dan ingin mendapatkan keahlian dalam ilmu data, lihat kursus ilmu data kami.

Ikhtisar Konten

Pengantar singkat tentang konsep Rantai Markov dan Properti Markov
Ekspresi matematis dan grafis dari Markov Chain
Python Markov Chain – mengkodekan contoh Markov Chain dengan Python

Pengantar Rantai Markov

Untuk menggunakan Rantai Markov Python untuk memecahkan masalah praktis, penting untuk memahami konsep Rantai Markov. Pada tahun 1906, matematikawan Rusia Andrei Markov memberikan definisi Rantai Markov – proses stokastik yang terdiri dari variabel acak yang bertransisi dari satu keadaan tertentu ke keadaan berikutnya, dan transisi ini didasarkan pada asumsi khusus dan aturan probabilistik.

Sebuah properti matematika dasar yang disebut Properti Markov adalah dasar dari transisi dari variabel acak. Dengan kata lain, Rantai Markov adalah deret variabel X1, X2, X3,…yang memenuhi Sifat Markov.

Prinsip Rantai Markov – Properti Markov

Rantai Markov didasarkan pada Properti Markov. Teori sifat Markov waktu diskrit menyatakan bahwa peluang suatu sistem acak berubah dari satu keadaan tertentu ke keadaan transisi berikutnya hanya bergantung pada keadaan dan waktu sekarang dan tidak bergantung pada keadaan sebelumnya.

Fakta bahwa kemungkinan keadaan masa depan dari proses acak tidak tergantung pada urutan keadaan yang ada sebelum membuat Rantai Markov menjadi proses tanpa memori yang hanya bergantung pada keadaan variabel saat ini.

Baca: Struktur Data Dibangun dengan Python

Ekspresi matematika dari Rantai Markov

Dalam hal distribusi probabilitas, asumsikan sebuah sistem pada contoh waktu 'n.' Menerapkan prinsip properti Markov, distribusi kondisional dari keadaan pada contoh waktu berikut, n+1, tidak bergantung pada keadaan sistem pada contoh waktu 1, 2, …, n-1.

Representasi grafis dari Markov Chain

Grafik berarah sering digunakan untuk mewakili Rantai Markov. Dalam grafik berarah, node menunjukkan kemungkinan keadaan yang berbeda dari variabel acak sementara tepi menunjukkan kemungkinan sistem berpindah dari satu keadaan ke keadaan lain dalam contoh waktu berikutnya. Untuk memahami representasinya, mari kita ambil contoh memprediksi cuaca. Asumsikan bahwa variabel acak adalah 'cuaca,' dan memiliki tiga kemungkinan keadaan yaitu. Cuaca = {cerah, hujan, bersalju}. Rantai Markov untuk skenario ini dapat direpresentasikan sebagai:

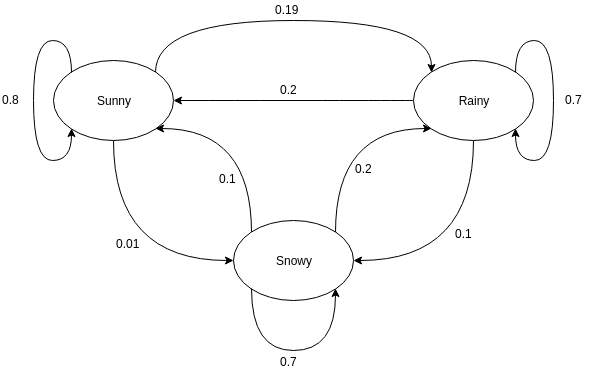
python rantai markov

Sumber

Dalam representasi grafis yang ditunjukkan di atas, katakanlah keadaan variabel acak yang diamati saat ini cerah. Probabilitas variabel acak yang mengambil nilai cerah pada saat berikutnya adalah 0,8. Bisa juga mengambil nilai bersalju dengan probabilitas 0,01, atau hujan dengan probabilitas 0,19. Hal penting yang perlu diperhatikan disini adalah bahwa nilai probabilitas yang ada pada suatu state akan selalu berjumlah 1.

Mengkodekan Rantai Markov dengan Python

Untuk lebih memahami Python Markov Chain , mari kita lihat contoh di mana contoh Markov Chain dikodekan dengan Python. Saat memecahkan masalah di dunia nyata, adalah praktik umum untuk menggunakan perpustakaan yang mengkodekan Rantai Markov secara efisien. Namun, mengkodekan Rantai Markov dengan Python adalah cara terbaik untuk memulai analisis dan simulasi Rantai Markov. Oleh karena itu muncullah utilitas dari Python Markov Chain . Mari kita lihat bagaimana contoh ramalan cuaca yang diberikan di bagian sebelumnya dapat dikodekan dengan Python. Mulailah dengan mendefinisikan kelas sederhana:

Setelah mendefinisikan kelas MarkovChain, mari kita coba mengkodekan contoh prediksi cuaca sebagai representasi cara kerja Python Markov Chain .

Sumber

Baca: Operator di Python

Parameterisasi Rantai Markov menggunakan Matriks Transisi

Di bagian sebelumnya, kode Python membuat parameter Rantai Markov menggunakan kamus yang berisi nilai probabilitas dari semua kemungkinan transisi status. Cara alternatif untuk merepresentasikan probabilitas transisi adalah dengan menggunakan matriks transisi, yang merupakan representasi standar, kompak, dan tabular dari Rantai Markov.

Dalam situasi di mana terdapat ratusan status, penggunaan Matriks Transisi lebih efisien daripada implementasi kamus. Kelas Rantai Markov dimodifikasi sebagai berikut untuk menerima matriks transisi:

Implementasi kamus mengulang nama negara bagian. Namun, dalam kasus Matriks Transisi, nilai probabilitas dalam metode next_state dapat diperoleh dengan menggunakan pengindeksan NumPy:

Sumber

Kesimpulan

Rantai Markov adalah alat matematika penting yang membantu menyederhanakan prediksi keadaan masa depan dari proses stokastik kompleks; itu semata-mata tergantung pada keadaan proses saat ini dan memandang masa depan sebagai independen dari masa lalu. Memanfaatkan Properti Markov, Python Markov Chain coding adalah cara yang efisien untuk memecahkan masalah praktis yang melibatkan sistem kompleks dan variabel dinamis.

Baik itu prakiraan cuaca, peringkat kredit, atau mengetik prediksi kata di ponsel Anda, Markov Chains memiliki aplikasi yang dibuat-buat dalam berbagai disiplin ilmu. Bergantung pada sifat parameter dan aplikasinya, ada berbagai konsep Rantai Markov. Python Markov Chain adalah cara yang logis dan efisien untuk mengimplementasikan Markov Chains dengan mengkodekannya dengan Python.

Jika Anda penasaran untuk belajar tentang python, ilmu data, lihat Program PG Eksekutif IIIT-B & upGrad dalam Ilmu Data yang dibuat untuk para profesional yang bekerja dan menawarkan 10+ studi kasus & proyek, lokakarya praktis, bimbingan dengan pakar industri , 1-on-1 dengan mentor industri, 400+ jam pembelajaran dan bantuan pekerjaan dengan perusahaan-perusahaan top.

Apa yang dimaksud dengan matriks transisi Markov?

Probabilitas keadaan tertentu berubah dari satu ke yang lain terkandung dalam matriks transisi, yang merupakan matriks persegi. Anda dapat menggunakan matriks transisi untuk melakukan perkalian matriks, mengidentifikasi pola, dan membuat prediksi dengan menggunakannya. Dalam sistem dinamis, matriks transisi Markov adalah matriks persegi yang menggambarkan probabilitas transisi dari satu keadaan ke keadaan lainnya. Probabilitas migrasi dari negara bagian yang diwakili oleh baris itu ke negara bagian lain tercantum di setiap baris. Akibatnya, setiap baris matriks transisi Markov berjumlah satu. Matriks transisi digunakan untuk menggambarkan bagaimana transisi antara dua keadaan dihasilkan. Ketika kejadian lebih atau kurang mungkin sebagai akibat dari peristiwa masa lalu, itu digunakan.

Bagaimana keadaan penyerapan rantai Markov?

Menurut teori probabilitas, rantai Markov penyerap adalah rantai di mana setiap keadaan dapat mencapai keadaan penyerap. Sebuah negara menyerap adalah salah satu yang Anda tidak bisa keluar dari setelah Anda memasukinya. Rantai Markov dikatakan menyerap jika setidaknya ada satu keadaan penyerap yang ada di dalamnya dan dimungkinkan untuk berpindah dari keadaan mana pun ke setidaknya satu keadaan penyerap dalam jumlah langkah yang terbatas. Keadaan sementara adalah keadaan yang tidak diserap oleh rantai penyerap Markov.

Apa itu Model Markov Tersembunyi (HMM)?

HMM adalah model matematika di mana sistem yang diperiksa adalah proses Markov dengan keadaan tersembunyi atau tidak teramati. Model Markov Tersembunyi digunakan dalam pembelajaran mesin dan aplikasi pengenalan pola seperti pengenalan gerakan dan pengenalan suara. Dalam model probabilistik, Model Markov Tersembunyi memungkinkan kita untuk berbicara tentang peristiwa yang terlihat atau tampak serta peristiwa yang tersembunyi. Ini juga membantu dalam penyelesaian masalah dunia nyata seperti masalah Natural Language Processing (NLP), Time Series, dan banyak lagi. Dalam HMM, dua asumsi utama dibuat. Pengamatan saat ini dan keadaan masa depan sepenuhnya bergantung pada keadaan saat ini.