Markov Chain in Python Tutorial
Pubblicato: 2020-03-26Sommario
Panoramica
Ti è mai passato per la mente come i meteorologi esperti fanno una previsione precisa del tempo o come Google classifica le diverse pagine web? Come realizzano le affascinanti applicazioni Python nel mondo reale. Questi calcoli sono complessi e coinvolgono diverse variabili che sono dinamiche e possono essere risolte utilizzando stime probabilistiche.
Qui sta l'idea di Markov Chains; ci sono stati individuali (diciamo, le condizioni meteorologiche) in cui ogni stato può cambiare casualmente in altri stati (una giornata piovosa può trasformarsi in una giornata di sole) e questi cambiamenti o transizioni sono basati sulla probabilità. Questo articolo fornisce una breve introduzione al concetto di Markov Chains e al modo in cui Python Markov Chain può essere utilizzato per codificare i modelli di Markov Chain in Python per risolvere problemi del mondo reale. Se sei un principiante e desideri acquisire esperienza nella scienza dei dati, dai un'occhiata ai nostri corsi di scienza dei dati.
Panoramica dei contenuti
- Una breve introduzione ai concetti di Markov Chain e Markov Property
- Espressione matematica e grafica di Markov Chain
- Python Markov Chain : codifica di esempi di Markov Chain in Python
Introduzione alla catena di Markov
Per utilizzare Python Markov Chain per risolvere problemi pratici, è essenziale comprendere il concetto di Markov Chains. Nel 1906, il matematico russo Andrei Markov diede la definizione di catena di Markov, un processo stocastico costituito da variabili casuali che passano da uno stato particolare all'altro e queste transizioni si basano su ipotesi specifiche e regole probabilistiche.
Una proprietà matematica fondamentale chiamata Proprietà di Markov è alla base delle transizioni delle variabili casuali. In altre parole, una catena di Markov è una serie di variabili X1, X2, X3,... che soddisfano la proprietà di Markov.
Principio della catena di Markov – Proprietà di Markov
Una catena Markov si basa sulla proprietà Markov. La teoria della proprietà di Markov a tempo discreto afferma che la probabilità che un sistema casuale cambi da uno stato particolare al successivo stato di transizione dipende solo dallo stato e dal tempo presenti ed è indipendente dagli stati precedenti.
Il fatto che il probabile stato futuro di un processo casuale sia indipendente dalla sequenza di stati che esistevano prima di esso rende la catena di Markov un processo senza memoria che dipende solo dallo stato corrente della variabile.
Leggi: Strutture di dati integrate in Python
L'espressione matematica della catena di Markov
In termini di distribuzione di probabilità, si assuma un sistema all'istanza di tempo 'n.' Applicando il principio della proprietà di Markov, la distribuzione condizionale degli stati alla seguente istanza temporale, n+1, è indipendente dagli stati del sistema alle istanze temporali 1, 2, …, n-1.
Rappresentazione grafica della catena di Markov
I grafici diretti sono spesso usati per rappresentare una catena di Markov. Nei grafici diretti, i nodi indicano diversi stati probabili delle variabili casuali mentre gli archi indicano la probabilità che il sistema si sposti da uno stato all'altro nell'istanza temporale successiva. Per comprendere la rappresentazione, prendiamo l'esempio della previsione del tempo. Si supponga che la variabile casuale sia 'meteo' e che abbia tre possibili stati, vale a dire. Tempo = {soleggiato, piovoso, nevoso}. La catena di Markov per questo scenario può essere rappresentata come:
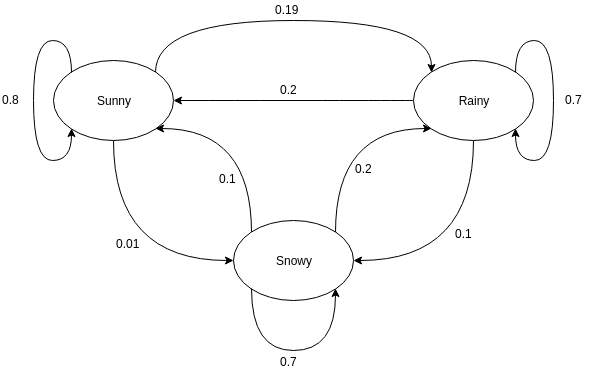
Fonte
Nella rappresentazione grafica mostrata sopra, supponiamo che lo stato attuale osservato della variabile casuale sia soleggiato. La probabilità che la variabile casuale assuma il valore sunny alla prossima istanza è 0,8. Può anche assumere il valore nevoso con una probabilità di 0,01 o piovoso con una probabilità di 0,19. Una cosa importante da notare qui è che i valori di probabilità esistenti in uno stato saranno sempre sommati a 1.
Codificare una catena di Markov in Python
Per comprendere meglio Python Markov Chain , esaminiamo un'istanza in cui un esempio di Markov Chain è codificato in Python. Durante la risoluzione dei problemi nel mondo reale, è pratica comune utilizzare una libreria che codifichi le catene di Markov in modo efficiente. Tuttavia, la codifica di Markov Chain in Python è un modo eccellente per iniziare l'analisi e la simulazione di Markov Chain. Da qui deriva l'utilità di Python Markov Chain . Vediamo come l'esempio di previsione meteo fornito nella sezione precedente può essere codificato in Python. Inizia definendo una classe semplice:


Dopo aver definito la classe MarkovChain, proviamo a codificare l'esempio di previsione meteorologica come rappresentazione di come funziona Python Markov Chain .

Fonte
Leggi: Operatori in Python
Parametrizzazione delle catene di Markov utilizzando la matrice di transizione
Nella sezione precedente, il codice Python ha parametrizzato la catena di Markov utilizzando un dizionario che conteneva i valori di probabilità di tutte le probabili transizioni di stato. Un modo alternativo per rappresentare le probabilità di transizione è utilizzare una matrice di transizione, che è una rappresentazione standard, compatta e tabellare di una catena di Markov.
In situazioni in cui sono presenti centinaia di stati, l'uso della matrice di transizione è più efficiente dell'implementazione di un dizionario. La classe Markov Chain viene modificata come segue per accettare una matrice di transizione:

L'implementazione del dizionario stava scorrendo i nomi degli stati. Tuttavia, nel caso di una matrice di transizione, i valori di probabilità nel metodo next_state possono essere ottenuti utilizzando l'indicizzazione NumPy:

Fonte
Conclusione
Le catene di Markov sono uno strumento matematico essenziale che aiuta a semplificare la previsione dello stato futuro di complessi processi stocastici; dipende esclusivamente dallo stato attuale del processo e vede il futuro come indipendente dal passato. Utilizzando la proprietà Markov, la codifica Python Markov Chain è un modo efficiente per risolvere problemi pratici che coinvolgono sistemi complessi e variabili dinamiche.
Che si tratti di previsioni meteorologiche, rating del credito o digitazione di parole sul tuo telefono cellulare, Markov Chains ha applicazioni inverosimili in un'ampia varietà di discipline. A seconda della natura dei parametri e dell'applicazione, esistono diversi concetti di Markov Chains. Python Markov Chain è un modo logico ed efficiente per implementare le catene di Markov codificandole in Python.
Se sei curioso di conoscere Python, la scienza dei dati, dai un'occhiata all'Executive PG Program in Data Science di IIIT-B e upGrad, creato per i professionisti che lavorano e offre oltre 10 casi di studio e progetti, workshop pratici pratici, tutoraggio con esperti del settore , 1 contro 1 con mentori del settore, oltre 400 ore di apprendimento e assistenza al lavoro con le migliori aziende.
Che cos'è una matrice di transizione di Markov?
La probabilità che particolari stati cambino dall'uno all'altro è contenuta in una matrice di transizione, che è una matrice quadrata. È possibile utilizzare una matrice di transizione per eseguire la moltiplicazione di matrici, identificare modelli e fare previsioni utilizzandola. In un sistema dinamico, una matrice di transizione di Markov è una matrice quadrata che descrive la probabilità di transizione da uno stato all'altro. La probabilità di migrare dallo stato rappresentato da quella riga agli altri stati è elencata in ogni riga. Di conseguenza, ogni riga di una matrice di transizione di Markov ne aggiunge uno. Le matrici di transizione vengono utilizzate per descrivere come vengono prodotte le transizioni tra due stati. Quando le occorrenze sono più o meno probabili come risultato di eventi passati, viene utilizzato.
Qual è lo stato assorbente della catena di Markov?
Secondo la teoria della probabilità, una catena di Markov assorbente è quella in cui ogni stato può raggiungere uno stato assorbente. Uno stato assorbente è quello da cui non puoi uscire dopo averlo inserito. Una catena di Markov si dice assorbente se in essa è presente almeno uno stato assorbente ed è possibile passare da qualsiasi stato ad almeno uno stato assorbente in un numero limitato di passaggi. Uno stato transitorio è quello che non è assorbito da una catena di Markov assorbente.
Cosa sono i modelli Markov nascosti (HMM)?
L'HMM è un modello matematico in cui il sistema esaminato è un processo di Markov con stati nascosti o non osservati. Il modello Hidden Markov viene utilizzato nelle applicazioni di apprendimento automatico e riconoscimento di modelli come il riconoscimento dei gesti e il riconoscimento vocale. Nel modello probabilistico, il Modello di Markov nascosto ci permette di parlare di eventi visti o apparenti così come di eventi nascosti. Aiuta anche nella risoluzione di problemi del mondo reale come problemi di elaborazione del linguaggio naturale (NLP), serie temporali e molti altri. In HMM vengono fatte due ipotesi chiave. L'osservazione presente e lo stato futuro dipendono completamente dallo stato attuale.
