Karar Ağacı Örneği: İşlev ve Uygulama [Adım Adım]

Tanıtım

Karar Ağaçları, hem regresyon hem de sınıflandırma görevleri için en güçlü ve popüler algoritmalardan biridir. Akış şeması benzeri bir yapıdır ve denetimli algoritmalar kategorisine girerler. Karar ağaçlarının bir akış şeması gibi görselleştirilebilmesi, insanların düşünme düzeylerini kolayca taklit etmelerini sağlar ve bu nedenle bu karar ağaçlarının kolayca anlaşılması ve yorumlanmasının nedeni budur.

Karar Ağacı nedir?

Karar Ağaçları, ağaç yapılı sınıflandırıcıların bir türüdür. Üç tür düğüme sahiptirler,

• Kök Düğümler
• Dahili Düğümler
• Yaprak Düğümleri

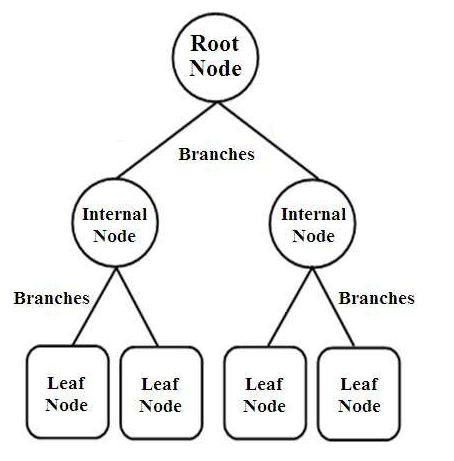
Görüntü Kaynağı

Kök düğümler, diğer birkaç düğüme ayrılan tüm örneği temsil eden birincil düğümlerdir. Dahili düğümler bir öznitelik üzerindeki testi temsil ederken, dallar testin kararını temsil eder. Son olarak, yaprak düğümler, tüm niteliklerin derlenmesinden sonra alınan karar olan etiketin sınıfını belirtir. Karar ağacı öğrenimi hakkında daha fazla bilgi edinin.

Karar Ağaçları nasıl çalışır?

Karar ağaçları, kök düğümden yaprak düğüme kadar tüm ağaç yapısını sıralayarak sınıflandırmada kullanılır. Karar ağacının kullandığı bu yaklaşıma Yukarıdan Aşağıya yaklaşım denir. Karar ağacına belirli bir veri noktası beslendikten sonra, belirlenen yaprak düğüme ulaşana kadar Evet/Hayır soruları yanıtlanarak ağacın her bir düğümünden geçmesi sağlanır.

Karar ağacındaki her düğüm, bir öznitelik için bir test durumunu temsil eder ve yeni bir düğüme yapılan her iniş (dal), o test senaryosunun olası cevaplarından birine karşılık gelir. Bu şekilde, birden çok yineleme ile karar ağacı, regresyon görevi için bir değer tahmin eder veya nesneyi bir sınıflandırma görevinde sınıflandırır.

Karar Ağacı Uygulaması

Artık bir karar ağacının temellerine sahip olduğumuza göre, Python programlamasında yürütülmesine geçelim.

Problem analizi

Aşağıdaki örnekte ünlü “İris Çiçeği” Veri Kümesini kullanacağız. İlk olarak 1936'da UCI Machine Learning Repository'de yayınlandı (Bağlantı: https://archive.ics.uci.edu/ml/datasets/Iris ), bu küçük veri seti, makine öğrenimi algoritmalarını ve görselleştirmelerini test etmek için yaygın olarak kullanılmaktadır.

Bunda 4 sütun nitelik veya özellikler olmak üzere toplam 150 satır ve 5 sütun vardır ve son sütun İris çiçek türü türüdür. İris, botanikte çiçekli bitkilerin bir cinsidir. Cm cinsinden dört öznitelik,

• Sepal Uzunluğu
• Sepal Genişliği
• Petal Uzunluğu
• Petal Genişliği

Bu dört özellik, boyut ve şekle bağlı olarak İris çiçeğinin türünü tanımlamak ve sınıflandırmak için kullanılır. 5. veya son sütun, Iris Setosa , Iris Versicolor ve Iris Virginica olan Iris çiçek sınıfından oluşur.

Problemimiz için, özellikleri öğrenmek ve onları İris çiçeği sınıfına göre sınıflandırmak için Karar Ağacı Algoritmasını kullanan bir Makine Öğrenimi modeli oluşturmamız gerekiyor.

Adım adım python'daki uygulamasını inceleyelim:

Adım 1: Kitaplıkları içe aktarma

Python'da herhangi bir makine öğrenimi modeli oluşturmanın ilk adımı, Numpy, Pandas ve Matplotlib gibi gerekli kitaplıkları içe aktarmak olacaktır. Ağaç modülü, sonunda Karar Ağacı modelini görselleştirmek için sklearn kitaplığından içe aktarılır.

2. Adım: Veri kümesini içe aktarma

Iris veri setini içe aktardıktan sonra, .csv dosyasını tablonun sütunlarına ve satırlarına kolayca erişebileceğimiz bir Pandas DataFrame'de saklarız. Veri çerçevesinin ilk dört sütunu, bağımsız değişkenler veya karar ağacı sınıflandırıcısı tarafından anlaşılması gereken ve X değişkeninde depolanan özelliklerdir.

3 türden oluşan İris çiçeği sınıfı olan bağımlı değişken, y değişkenine depolanır. İlk 5 satır yazdırılarak veri seti görselleştirilir.

Ayrıca Okuyun: Karar Ağacı Sınıflandırması

Adım 3: Veri kümesini Eğitim kümesi ve Test kümesine bölme

Bir sonraki adımda, veri setini okuduktan sonra, tüm veri setini, sınıflandırıcı modelin eğitileceği eğitim seti ve eğitilen modelin uygulanacağı test seti olarak ayırmamız gerekiyor. Test setinde elde edilen sonuçlar, eğitilen modelin doğruluğunu kontrol etmek için karşılaştırılacaktır.

Burada, tüm veri setinin %25'inin rastgele olarak test seti olarak bölüneceğini ve kalan %75'inin modelin eğitiminde kullanılacak eğitim setinden oluşacağını ifade eden 0.25'lik bir test boyutu kullandık. Bu nedenle, 150 veri noktasından 38 rastgele veri noktası test seti olarak tutulur ve kalan 112 örnek eğitim setinde kullanılır.

Adım 4: Karar Ağacı Sınıflandırma modelinin Eğitim Seti üzerinde eğitilmesi

Model bölündüğünde ve eğitim amacıyla hazır olduğunda, DecisionTreeClassifier modülü sklearn kitaplığından içe aktarılır ve modeli oluşturmak için eğitim değişkenleri (X_train ve y_train) sınıflandırıcıya takılır. Bu eğitim sürecinde, sınıflandırıcı Gradient Descent ve Backpropagation gibi çeşitli optimizasyon yöntemlerinden geçer ve son olarak Karar Ağacı Sınıflandırıcı modelini oluşturur.

Adım 5: Test Seti Sonuçlarını Tahmin Etme

Modelimiz hazır olduğuna göre test setinde doğruluğunu kontrol etmemiz gerekmez mi? Bu adım, daha önce bölünmüş olan test setinde karar ağacı algoritması kullanılarak oluşturulan modelin test edilmesini içerir. Bu sonuçlar “y_pred” değişkeninde saklanır.

Adım 6: Gerçek Değerlerin Öngörülen Değerlerle Karşılaştırılması

Bu, bir tarafta test setinin gerçek değerleri ve diğer tarafta tahmin edilen değerler olmak üzere iki sütundan oluşacak başka bir basit veri çerçevesi oluşturacağımız başka bir basit adımdır. Bu adım, oluşturulan model tarafından elde edilen sonuçları karşılaştırmamızı sağlar.

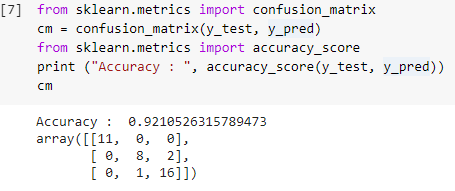
Adım 7: Karışıklık Matrisi ve Doğruluk

Artık test setlerinin hem gerçek hem de tahmin edilen değerlerine sahip olduğumuza göre, basit bir sınıflandırma matrisi oluşturalım ve sklearn içinde basit kütüphane fonksiyonları kullanılarak oluşturulan modelimizin doğruluğunu hesaplayalım. Doğruluk puanı, test setinin hem gerçek hem de tahmin edilen değerleri girilerek hesaplanır. Yukarıdaki adımlar kullanılarak oluşturulan model, bize aşağıdaki adımda 0.92105 olarak gösterilen %92,1'lik bir doğruluk verir.

Karışıklık matrisi, bir sınıflandırma probleminde doğru ve yanlış tahminleri göstermek için kullanılan bir tablodur. Basit kullanım için, köşegen üzerindeki değerler doğru tahminleri temsil eder ve köşegen dışındaki diğer değerler yanlış tahminlerdir.

38 test seti veri noktasından sayıyı hesaplarken, %92 doğru olarak yansıtılan 35 doğru tahmin ve 3 yanlış tahmin elde ederiz. Modeli eğitmeden önce sınıflandırıcıya argüman olarak verilebilecek hiperparametreleri optimize ederek doğruluk artırılabilir.

Adım 8: Karar Ağacı Sınıflandırıcısını Görselleştirme

Son adımda, oluşturulan Karar Ağacını görselleştireceğiz. Kök düğüm fark edildiğinde, daha önce bölünmüş eğitim seti örnekleriyle senkronize olan “örnek” sayısının 112 olduğu görülmektedir. Karar ağacı algoritmasının her adımında GINI indeksi hesaplanır ve karar ağacındaki “değer” parametresinde gösterildiği gibi 3 sınıf bölünür.

Mutlaka Okuyun: Karar Ağacı Mülakat Soruları ve Cevapları

Çözüm

Dolayısıyla, bu şekilde Karar Ağacı algoritması kavramını anladık ve bu algoritmayı kullanarak bir sınıflandırma problemini çözmek için basit bir Sınıflandırıcı oluşturduk.

Karar ağaçları, makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, IIIT-B & upGrad'ın çalışan profesyoneller için tasarlanmış ve 450+ saatlik zorlu eğitim, 30'dan fazla vaka çalışması ve ödev sunan Makine Öğrenimi ve Yapay Zeka alanında PG Diplomasına göz atın , IIIT-B Mezunları statüsü, 5'ten fazla pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.