Функциональность регрессии дерева решений, термины, реализация [с примером]

Начнем с того, что регрессионная модель — это модель, которая выдает на выходе числовое значение, если заданы некоторые входные значения, которые также являются числовыми. Это отличается от того, что делает модель классификации. Он классифицирует тестовые данные по различным классам или группам, участвующим в данной постановке задачи.

Размер группы может быть от 2 до 1000 и более. Существует множество моделей регрессии, таких как линейная регрессия, многомерная регрессия, регрессия Риджа, логистическая регрессия и многие другие. Регрессионные модели дерева решений также относятся к этому пулу регрессионных моделей.

Модель прогнозирования либо классифицирует, либо прогнозирует числовое значение, используя бинарные правила для определения выходного или целевого значения. Модель дерева решений, как следует из названия, представляет собой древовидную модель с листьями, ветвями и узлами.

Изучите онлайн-курс по машинному обучению от лучших университетов мира. Заработайте программы Masters, Executive PGP или Advanced Certificate Programs, чтобы ускорить свою карьеру.

Читайте: Идеи проекта машинного обучения

Термины, которые следует помнить

Прежде чем мы углубимся в алгоритм, вот несколько важных терминов, которые вы все должны знать.

1. Корневой узел: это самый верхний узел, с которого начинается разделение.
2. Разделение: процесс разделения одного узла на несколько подузлов.
3. Конечный узел или листовой узел: узлы, которые не разделяются дальше, называются конечными узлами.
4. Обрезка: процесс удаления подузлов.
5. Родительский узел: узел, который далее разбивается на подузлы.
6. Дочерний узел: подузлы, возникшие из родительского узла.

Как это работает?

Дерево решений разбивает набор данных на более мелкие подмножества. Лист решения разбивается на две или более ветвей, которые представляют значение исследуемого атрибута. Самый верхний узел в дереве решений является лучшим предиктором, называемым корневым узлом. ID3 — это алгоритм, который строит дерево решений.

Он использует подход сверху вниз, а разделение производится на основе стандартного отклонения. Просто для быстрого пересмотра, стандартное отклонение — это степень распределения или дисперсии набора точек данных от его среднего значения. Он количественно определяет общую изменчивость распределения данных.

Более высокое значение дисперсии или изменчивости означает большее стандартное отклонение, указывающее на больший разброс точек данных от среднего значения. Мы используем стандартное отклонение для измерения однородности выборки. Если образец полностью однороден, его стандартное отклонение равно нулю.

И аналогично, чем выше степень неоднородности, тем больше будет стандартное отклонение. Среднее значение выборки и количество выборок необходимы для расчета стандартного отклонения. Мы используем математическую функцию — Коэффициент отклонения, который определяет, когда следует прекратить разделение. Он рассчитывается путем деления стандартного отклонения на среднее значение всех выборок.

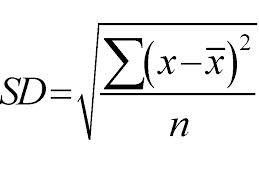
Источник

Окончательное значение будет средним значением конечных узлов. Скажем, например, если ноябрь — это узел, который далее разбивается на различные зарплаты в течение многих лет в ноябре (до 2020 года). В 2021 году зарплата за ноябрь будет средней из всех зарплат в узле ноябрь.

Переходим к стандартному отклонению двух классов или атрибутов (как в приведенном выше примере, заработная плата может быть основана либо на почасовой, либо на месячной основе). Формула будет выглядеть следующим образом:

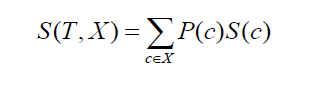
Источник

где P(c) — вероятность появления атрибута c, S(c) — соответствующее стандартное отклонение атрибута c. Метод уменьшения стандартного отклонения основан на уменьшении стандартного отклонения после разделения набора данных.

Чтобы построить точное дерево решений, цель должна состоять в том, чтобы найти атрибуты, которые возвращаются при вычислении, и возвращают самое высокое уменьшение стандартного отклонения. Простыми словами, самые однородные ветки.

Процесс создания дерева решений для регрессии включает четыре важных этапа.

1. Во-первых, мы вычисляем стандартное отклонение целевой переменной. Предположим, что целевой переменной является зарплата, как в предыдущих примерах. Имея пример, мы рассчитаем стандартное отклонение набора значений заработной платы.

2. На шаге 2 набор данных дополнительно разбивается на разные атрибуты. говоря об атрибутах, поскольку целевое значение — это зарплата, мы можем думать о возможных атрибутах как — месяцы, часы, настроение начальника, должность, год в компании и так далее. Затем стандартное отклонение для каждой ветви рассчитывается по приведенной выше формуле. полученное таким образом стандартное отклонение вычитается из стандартного отклонения перед разделением. Полученный результат называется уменьшением стандартного отклонения.

3. После того, как разница будет рассчитана, как указано на предыдущем шаге, лучшим атрибутом будет тот, для которого значение уменьшения стандартного отклонения наибольшее. Это означает, что стандартное отклонение до разделения должно быть больше, чем стандартное отклонение до разделения. Собственно, мод разницы берется и так наоборот тоже можно.

4. Весь набор данных классифицируется на основе важности выбранного атрибута. На неконечных ветвях этот метод рекурсивно продолжается до тех пор, пока не будут обработаны все доступные данные. Теперь рассмотрим, что месяц выбран как лучший атрибут разделения на основе значения уменьшения стандартного отклонения. Таким образом, у нас будет 12 филиалов на каждый месяц. Эти ветви будут дополнительно разделены, чтобы выбрать лучший атрибут из оставшегося набора атрибутов.

5. На самом деле нам нужны некоторые критерии отделки. Для этого мы используем коэффициент отклонения или CV для ветви, которая становится меньше определенного порога, например 10%. Когда мы достигаем этого критерия, мы останавливаем процесс построения дерева. Поскольку дальнейшего разделения не происходит, значение, подпадающее под этот атрибут, будет средним значением всех значений в этом узле.

Реализация

Регрессия дерева решений может быть реализована с использованием языка Python и библиотеки scikit-learn. Его можно найти в sklearn.tree.DecisionTreeRegressor.

Вот некоторые из важных параметров:

1. Критерий: Для измерения качества разделения. Его значение может быть «mse» или среднеквадратической ошибкой, «friedman_mse» и «mae» или средней абсолютной ошибкой. Значение по умолчанию — mse.
2. max_depth: представляет максимальную глубину дерева. Значение по умолчанию — Нет.
3. max_features: представляет количество функций, которые следует искать при выборе наилучшего разделения. Значение по умолчанию — Нет.
4. splitter: этот параметр используется для выбора разделения на каждом узле. Доступные значения: «лучший» и «случайный». Лучшее значение по умолчанию.

Проверьте: Вопросы для интервью по машинному обучению

Пример из документации sklearn

>>> из sklearn.datasets импортировать load_diabetes

>>> из sklearn.model_selection импортировать cross_val_score

>>> из sklearn.tree импортировать DecisionTreeRegressor

>>> X, y = load_diabetes (return_X_y = True )

>>> регрессор = DecisionTreeRegressor(random_state=0)

>>> cross_val_score (регрессор, X, y, cv=10)

… # доктест: +ПРОПУСТИТЬ

…

массив([-0,39…, -0,46…, 0,02…, 0,06…, -0,50…,

0,16…, 0,11…, -0,73…, -0,30…, -0,00…])

Что дальше?

Кроме того, если вам интересно узнать больше о машинном обучении, ознакомьтесь с программой Executive PG IIIT-B и upGrad по машинному обучению и искусственному интеллекту, которая предназначена для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий. , статус выпускника IIIT-B, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.