Validare încrucișată în Python: tot ce trebuie să știți

În Data Science, validarea este probabil una dintre cele mai importante tehnici utilizate de Data Scientists pentru a valida stabilitatea modelului ML și pentru a evalua cât de bine s-ar generaliza la date noi. Validarea asigură că modelul ML preia modelele corecte (relevante) din setul de date în timp ce anulează cu succes zgomotul din setul de date. În esență, scopul tehnicilor de validare este de a se asigura că modelele ML au un factor de varianță de părtinire scăzut.

Astăzi vom discuta pe larg despre o astfel de tehnică de validare a modelului – validarea încrucișată.

Ce este validarea încrucișată?

Validarea încrucișată este o tehnică de validare concepută pentru a evalua și a evalua modul în care rezultatele analizei statistice (modelul) se vor generaliza la un set de date independent. Validarea încrucișată este utilizată în primul rând în scenariile în care predicția este scopul principal, iar utilizatorul dorește să estimeze cât de bine și de exactitate va funcționa un model predictiv în situații reale.

Validarea încrucișată urmărește să definească un set de date prin testarea modelului în faza de antrenament pentru a ajuta la minimizarea problemelor precum supraajustarea și subadaptarea. Totuși, trebuie să rețineți că atât validarea, cât și setul de antrenament trebuie extrase din aceeași distribuție, altfel ar duce la probleme în faza de validare.

Învață curs de certificare în știința datelor de la cele mai bune universități din lume. Câștigă programe Executive PG, programe avansate de certificat sau programe de master pentru a-ți accelera cariera.

Beneficiile validării încrucișate

• Ajută la evaluarea calității modelului dvs.
• Ajută la reducerea/evitarea problemelor de supraadaptare și subadaptare.
• Vă permite să selectați modelul care va oferi cea mai bună performanță pe date nevăzute.

Citiți: Proiecte Python pentru începători

Ce sunt supraajustarea și underfitting?

Supraadaptarea se referă la condiția în care un model devine prea sensibil la date și ajunge să capteze mult zgomot și modele aleatorii care nu se generalizează bine la datele nevăzute. În timp ce un astfel de model funcționează de obicei bine pe setul de antrenament, performanța sa suferă pe setul de testare.

Underfitting se referă la problema când modelul nu reușește să capteze suficiente modele în setul de date, oferind astfel o performanță slabă atât pentru antrenament, cât și pentru setul de testare.

Mergând pe lângă aceste două extremități, modelul perfect este unul care funcționează la fel de bine atât pentru antrenament, cât și pentru seturile de testare.

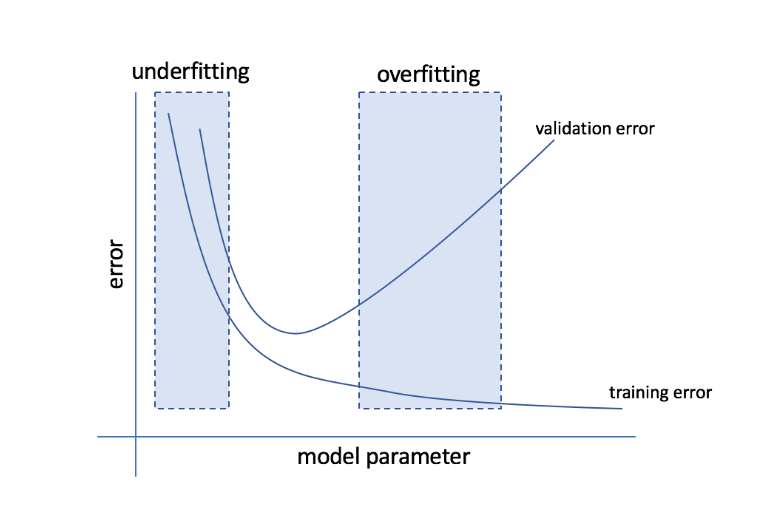
Sursă

Validare încrucișată: strategii de validare diferite

Strategiile de validare sunt clasificate în funcție de numărul de împărțiri efectuate într-un set de date. Acum, să ne uităm la diferitele strategii de validare încrucișată în Python.

1. Set de validare

Această abordare de validare împarte setul de date în două părți egale - în timp ce 50% din setul de date este rezervat pentru validare, restul de 50% este rezervat pentru antrenamentul modelului. Deoarece această abordare antrenează modelul pe baza doar a 50% dintr-un set de date dat, rămâne întotdeauna posibilitatea de a pierde informații relevante și semnificative ascunse în celelalte 50% din date. Ca rezultat, această abordare creează, în general, o părtinire mai mare în model.

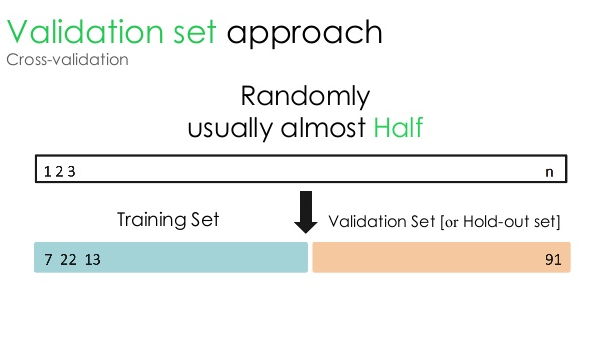
Sursă

Cod Python:

tren, validare = train_test_split(date, test_size=0,50, random_state = 5)

2. Împărțire tren/test

În această abordare de validare, setul de date este împărțit în două părți - set de antrenament și set de testare. Acest lucru se face pentru a evita orice suprapunere între setul de antrenament și setul de testare (dacă seturile de antrenament și de testare se suprapun, modelul va fi defect). Prin urmare, este esențial să ne asigurăm că setul de date utilizat pentru model nu trebuie să conțină probe duplicate în setul nostru de date. Strategia de împărțire tren/test vă permite să vă reantrenați modelul pe baza întregului set de date, fără a modifica niciun hiperparametru ai modelului.

Sursă

Cu toate acestea, această abordare are o limitare semnificativă – performanța și acuratețea modelului depind în mare măsură de modul în care este împărțit. De exemplu, dacă împărțirea nu este aleatorie sau un subset al setului de date are doar o parte din informațiile complete, va duce la supraadaptare. Cu această abordare, nu puteți fi sigur care puncte de date vor fi în care set de validare, creând astfel rezultate diferite pentru diferite seturi. Prin urmare, strategia de împărțire tren/test ar trebui utilizată numai atunci când aveți suficiente date la îndemână.

Cod Python:

>>> din sklearn.model_selection import train_test_split

>>> X, y = np.arange(10).reshape((5, 2)), range(5)

>>> X

matrice([[0, 1],

[2, 3],

[4, 5],

[6, 7],

[8, 9]])

>>> lista(y)

[0, 1, 2, 3, 4]

3. K-fold

După cum s-a văzut în cele două strategii anterioare, există posibilitatea de a pierde informații importante din setul de date, ceea ce crește probabilitatea de eroare sau supraadaptare indusă de părtinire. Acest lucru necesită o metodă care rezerve date abundente pentru antrenamentul modelului, lăsând totodată date suficiente pentru validare.

Introduceți tehnica de validare K-fold. În această strategie, setul de date este împărțit în „k” număr de subseturi sau pliuri, în care k-1 subseturi sunt rezervate pentru antrenamentul modelului, iar ultimul subset este utilizat pentru validare (set de testare). Modelul este mediatizat față de pliurile individuale și apoi finalizat. Odată ce modelul este finalizat, îl puteți testa folosind setul de testare.

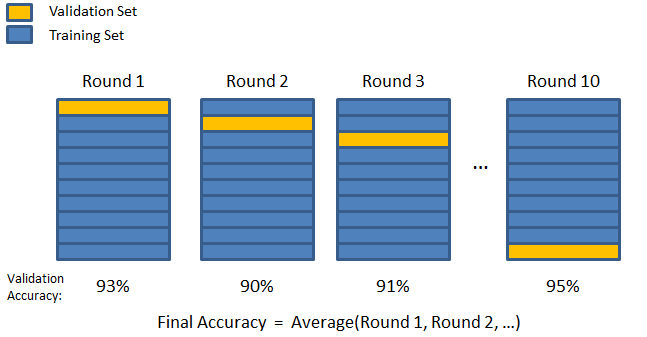
Sursă

Aici, fiecare punct de date apare în setul de validare exact o dată în timp ce rămâne în setul de antrenament k-1 de un număr de ori. Deoarece majoritatea datelor sunt folosite pentru montare, problema montajului insuficient se reduce semnificativ. În mod similar, problema supraajustării este eliminată, deoarece majoritatea datelor sunt utilizate și în setul de validare.

Citiți: Python vs Ruby: comparație completă alăturată

Strategia K-fold este cea mai bună pentru cazurile în care aveți o cantitate limitată de date și există o diferență substanțială în calitatea pliurilor sau diferiți parametri optimi între ele.

Cod Python:

din sklearn.model_selection import KFold # import KFold

X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]]) # creați o matrice

y = np.array([1, 2, 3, 4]) # Creați o altă matrice

kf = KFold(n_splits=2) # Definiți împărțirea – în 2 ori

kf.get_n_splits(X) # returnează numărul de iterații de împărțire în validatorul încrucișat

imprimare (kf)

KFold(n_splits=2, random_state=Niciunul, shuffle=False)

4. Lasă unul afară

Validarea încrucișată (LOOCV) este un caz special de K-fold atunci când k este egal cu numărul de eșantioane dintr-un anumit set de date. Aici, un singur punct de date este rezervat pentru setul de testare, iar restul setului de date este setul de antrenament. Deci, dacă utilizați obiectul „k-1” ca mostre de antrenament și obiectul „1” ca set de testare, acestea vor continua să itereze prin fiecare eșantion din setul de date. Este cea mai utilă metodă atunci când există prea puține date disponibile.

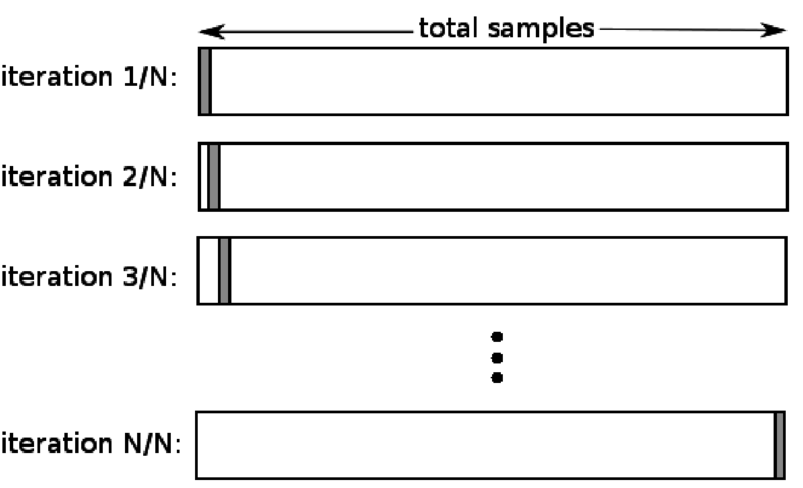
Sursă

Deoarece această abordare utilizează toate punctele de date, părtinirea este de obicei scăzută. Cu toate acestea, deoarece procesul de validare este repetat de „n” de ori (n=număr de puncte de date), duce la un timp de execuție mai mare. O altă constrângere notabilă a metodelor este că poate duce la o variație mai mare în testarea eficienței modelului pe măsură ce testați modelul față de un punct de date. Deci, dacă acel punct de date este un outlier, va crea un coeficient de variație mai mare.

Cod Python:

>>> import numpy ca np

>>> din sklearn.model_selection import LeaveOneOut

>>> X = np.array([[1, 2], [3, 4]])

>>> y = np.array([1, 2])

>>> loo = LeaveOneOut()

>>> loo.get_n_splits(X)

2

>>> print(too)

LeaveOneOut()

>>> pentru train_index, test_index în loo.split(X):

… print(„TRAIN:”, tren_index, „TEST:”, test_index)

… X_train, X_test = X[train_index], X[test_index]

… y_train, y_test = y[train_index], y[test_index]

… print(X_train, X_test, y_train, y_test)

TREN: [1] TEST: [0]

[[3 4]] [[1 2]] [2] [1]

TREN: [0] TEST: [1]

[[1 2]] [[3 4]] [1] [2]

5. Stratificare

De obicei, pentru împărțirea tren/test și K-fold, datele sunt amestecate pentru a crea o împărțire aleatorie de antrenament și validare. Astfel, permite o distribuție diferită a țintei în diferite pliuri. În mod similar, stratificarea facilitează, de asemenea, distribuția țintei pe diferite pliuri în timp ce împărțim datele.

În acest proces, datele sunt rearanjate în diferite pliuri într-un mod care să asigure fiecare pliază să devină un reprezentant al întregului. Deci, dacă aveți de-a face cu o problemă de clasificare binară în care fiecare clasă constă din 50% din date, puteți utiliza stratificarea pentru a aranja datele astfel încât fiecare clasă să includă jumătate din cazuri.

Procesul de stratificare este cel mai potrivit pentru seturile de date mici și neechilibrate cu clasificare multiclasă.

Cod Python:

din sklearn.model_selection import StratifiedKFold

skf = StratifiedKFold(n_splits=5, random_state=Nimic)

# X este setul de caracteristici și y este ținta

pentru train_index, test_index în skf.split(X,y):

print(„Tren:”, tren_index, „Validare:”, val_index)

X_train, X_test = X[train_index], X[val_index]

y_train, y_test = y[train_index], y[val_index]

Citiți: Cadre de date în Python – Tutorial

Când să utilizați fiecare dintre aceste cinci strategii de validare încrucișată?

După cum am menționat anterior, fiecare tehnică de validare încrucișată are cazuri de utilizare unice și, prin urmare, funcționează cel mai bine atunci când sunt aplicate corect în scenariile potrivite. De exemplu, dacă aveți suficiente date, iar scorurile și parametrii optimi (ai modelului) pentru diferite împărțiri sunt probabil să fie similare, abordarea împărțirii tren/test va funcționa excelent.

Cu toate acestea, dacă scorurile și parametrii optimi variază pentru diferite împărțiri, tehnica K-fold va fi cea mai bună. Pentru cazurile în care aveți prea puține date, abordarea LOOCV funcționează cel mai bine, în timp ce, pentru seturi de date mici și neechilibrate, stratificarea este calea de urmat.

Sperăm că acest articol detaliat v-a ajutat să obțineți o idee aprofundată despre validarea încrucișată în Python.

Dacă sunteți curios să aflați despre știința datelor, consultați programul Executive PG în știința datelor de la IIIT-B și upGrad, care este creat pentru profesioniști care lucrează și oferă peste 10 studii de caz și proiecte, ateliere practice practice, mentorat cu experți din industrie, 1 -on-1 cu mentori din industrie, peste 400 de ore de învățare și asistență profesională cu firme de top.