Validación cruzada en Python: todo lo que necesita saber sobre

En Data Science, la validación es probablemente una de las técnicas más importantes utilizadas por los científicos de datos para validar la estabilidad del modelo ML y evaluar qué tan bien se generalizaría a nuevos datos. La validación garantiza que el modelo ML recoja los patrones correctos (relevantes) del conjunto de datos mientras cancela con éxito el ruido en el conjunto de datos. Esencialmente, el objetivo de las técnicas de validación es asegurarse de que los modelos ML tengan un factor de varianza de sesgo bajo.

Hoy vamos a discutir extensamente sobre una de esas técnicas de validación de modelos: la validación cruzada.

¿Qué es la validación cruzada?

La validación cruzada es una técnica de validación diseñada para evaluar cómo los resultados del análisis estadístico (modelo) se generalizarán a un conjunto de datos independiente. La validación cruzada se usa principalmente en escenarios donde la predicción es el objetivo principal, y el usuario desea estimar qué tan bien y con precisión se desempeñará un modelo predictivo en situaciones del mundo real.

La validación cruzada busca definir un conjunto de datos probando el modelo en la fase de entrenamiento para ayudar a minimizar problemas como el sobreajuste y el ajuste insuficiente. Sin embargo, debe recordar que tanto la validación como el conjunto de entrenamiento deben extraerse de la misma distribución, o de lo contrario generaría problemas en la fase de validación.

Aprenda el curso de certificación de ciencia de datos de las mejores universidades del mundo. Obtenga programas Executive PG, programas de certificados avanzados o programas de maestría para acelerar su carrera.

Beneficios de la validación cruzada

• Ayuda a evaluar la calidad de su modelo.
• Ayuda a reducir/evitar problemas de overfitting y underfitting.
• Le permite seleccionar el modelo que ofrecerá el mejor rendimiento en datos no vistos.

Leer: Proyectos de Python para principiantes

¿Qué son el overfitting y el underfitting?

El sobreajuste se refiere a la condición en la que un modelo se vuelve demasiado sensible a los datos y termina capturando mucho ruido y patrones aleatorios que no se generalizan bien a los datos invisibles. Si bien un modelo de este tipo suele funcionar bien en el conjunto de entrenamiento, su rendimiento se ve afectado en el conjunto de prueba.

El ajuste insuficiente se refiere al problema cuando el modelo no logra capturar suficientes patrones en el conjunto de datos, lo que genera un rendimiento deficiente tanto para el conjunto de entrenamiento como para el de prueba.

A juzgar por estos dos extremos, el modelo perfecto es aquel que funciona igual de bien tanto para el entrenamiento como para la prueba.

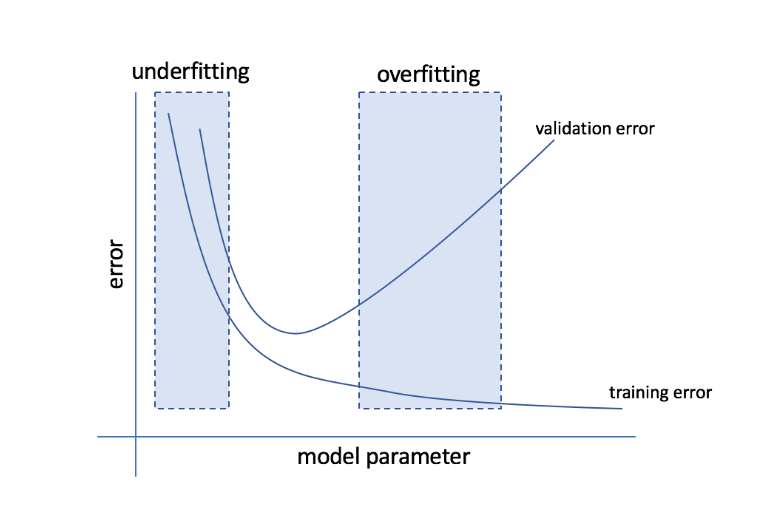
Fuente

Validación cruzada: diferentes estrategias de validación

Las estrategias de validación se clasifican en función del número de divisiones realizadas en un conjunto de datos. Ahora, veamos las diferentes estrategias de validación cruzada en Python.

1. Conjunto de validación

Este enfoque de validación divide el conjunto de datos en dos partes iguales: mientras que el 50 % del conjunto de datos se reserva para la validación, el 50 % restante se reserva para el entrenamiento del modelo. Dado que este enfoque entrena el modelo basándose solo en el 50 % de un conjunto de datos dado, siempre existe la posibilidad de perder información relevante y significativa oculta en el otro 50 % de los datos. Como resultado, este enfoque generalmente crea un mayor sesgo en el modelo.

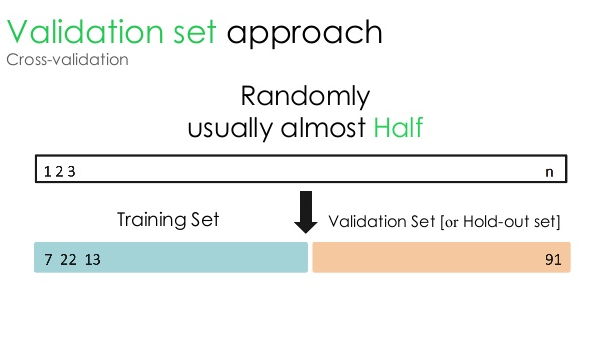
Fuente

código pitón:

tren, validación = train_test_split(datos, test_size=0.50, random_state = 5)

2. División de entrenamiento/prueba

En este enfoque de validación, el conjunto de datos se divide en dos partes: conjunto de entrenamiento y conjunto de prueba. Esto se hace para evitar cualquier superposición entre el conjunto de entrenamiento y el conjunto de prueba (si los conjuntos de entrenamiento y prueba se superponen, el modelo será defectuoso). Por lo tanto, es crucial asegurarse de que el conjunto de datos utilizado para el modelo no contenga muestras duplicadas en nuestro conjunto de datos. La estrategia de división de entrenamiento/prueba le permite volver a entrenar su modelo en función de todo el conjunto de datos sin alterar ningún hiperparámetro del modelo.

Fuente

Sin embargo, este enfoque tiene una limitación importante: el rendimiento y la precisión del modelo dependen en gran medida de cómo se divida. Por ejemplo, si la división no es aleatoria, o si un subconjunto del conjunto de datos tiene solo una parte de la información completa, se producirá un sobreajuste. Con este enfoque, no puede estar seguro de qué puntos de datos estarán en qué conjunto de validación, por lo que se crean diferentes resultados para diferentes conjuntos. Por lo tanto, la estrategia de división de entrenamiento/prueba solo debe usarse cuando tenga suficientes datos a mano.

código pitón:

>>> de sklearn.model_selection import train_test_split

>>> X, y = np.arange(10).reforma((5, 2)), range(5)

>>> X

matriz([[0, 1],

[2, 3],

[4, 5],

[6, 7],

[8, 9]])

>>> lista(y)

[0, 1, 2, 3, 4]

3. Plegado en K

Como se vio en las dos estrategias anteriores, existe la posibilidad de perder información importante en el conjunto de datos, lo que aumenta la probabilidad de error inducido por sesgo o sobreajuste. Esto requiere un método que reserve abundantes datos para el entrenamiento del modelo y al mismo tiempo deje suficientes datos para la validación.

Introduzca la técnica de validación K-fold. En esta estrategia, el conjunto de datos se divide en un número 'k' de subconjuntos o pliegues, donde los subconjuntos k-1 se reservan para el entrenamiento del modelo y el último subconjunto se usa para la validación (conjunto de prueba). El modelo se promedia contra los pliegues individuales y luego se finaliza. Una vez finalizado el modelo, puede probarlo utilizando el conjunto de prueba.

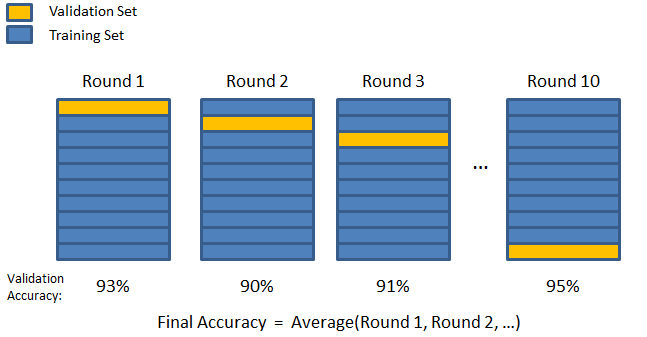
Fuente

Aquí, cada punto de datos aparece en el conjunto de validación exactamente una vez mientras permanece en el conjunto de entrenamiento k-1 número de veces. Dado que la mayoría de los datos se utilizan para el ajuste, el problema del ajuste insuficiente se reduce significativamente. De manera similar, se elimina el problema del sobreajuste, ya que la mayoría de los datos también se utilizan en el conjunto de validación.

Leer: Python vs Ruby: comparación completa lado a lado

La estrategia K-fold es mejor para los casos en los que tiene una cantidad limitada de datos y hay una diferencia sustancial en la calidad de los pliegues o diferentes parámetros óptimos entre ellos.

código pitón:

de sklearn.model_selection importar KFold # importar KFold

X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]]) # crear una matriz

y = np.array([1, 2, 3, 4]) # Crea otra matriz

kf = KFold(n_splits=2) # Define la división – en 2 pliegues

kf.get_n_splits(X) # devuelve el número de iteraciones de división en el validador cruzado

imprimir (kf)

KFold(n_splits=2, estado_aleatorio=Ninguno, barajar=Falso)

4. Deja uno fuera

La validación cruzada de exclusión (LOOCV) es un caso especial de K-fold cuando k es igual al número de muestras en un conjunto de datos en particular. Aquí, solo se reserva un punto de datos para el conjunto de prueba, y el resto del conjunto de datos es el conjunto de entrenamiento. Entonces, si usa el objeto "k-1" como muestras de entrenamiento y el objeto "1" como conjunto de prueba, continuarán iterando a través de cada muestra en el conjunto de datos. Es el método más útil cuando hay muy pocos datos disponibles.

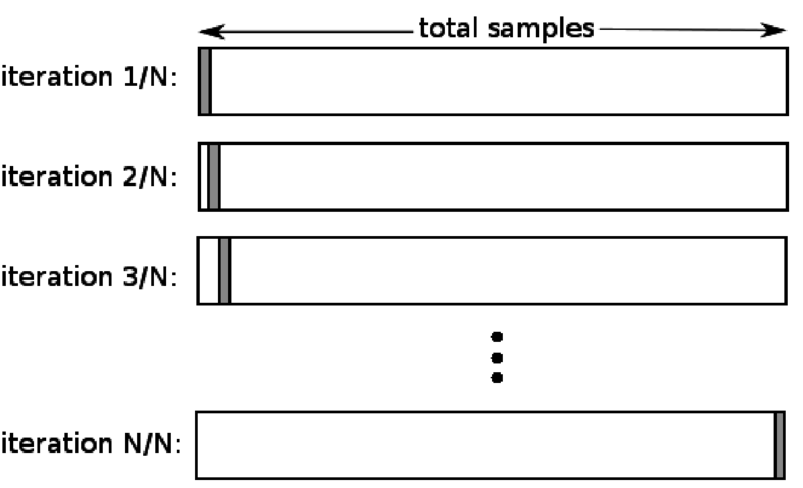
Fuente

Dado que este enfoque utiliza todos los puntos de datos, el sesgo suele ser bajo. Sin embargo, como el proceso de validación se repite 'n' veces (n=número de puntos de datos), conduce a un mayor tiempo de ejecución. Otra limitación notable de los métodos es que puede conducir a una mayor variación en la efectividad del modelo de prueba a medida que prueba el modelo contra un punto de datos. Entonces, si ese punto de datos es un valor atípico, creará un cociente de variación más alto.

código pitón:

>>> importar numpy como np

>>> de sklearn.model_selection importar LeaveOneOut

>>> X = np.matriz([[1, 2], [3, 4]])

>>> y = np.matriz([1, 2])

>>> loo = Deja UnoFuera()

>>> loo.get_n_splits(X)

2

>>> imprimir(baño)

DejarUnoFuera()

>>> for train_index, test_index en loo.split(X):

… print(“TREN:”, índice_tren, “PRUEBA:”, índice_prueba)

… X_tren, X_prueba = X[tren_índice], X[prueba_índice]

… y_tren, y_prueba = y[índice_tren], y[índice_prueba]

… imprimir(X_tren, X_prueba, y_tren, y_prueba)

TREN: [1] PRUEBA: [0]

[[3 4]] [[1 2]] [2] [1]

TREN: [0] PRUEBA: [1]

[[1 2]] [[3 4]] [1] [2]

5. estratificación

Por lo general, para la división de entrenamiento/prueba y el K-fold, los datos se mezclan para crear una división aleatoria de capacitación y validación. Por lo tanto, permite diferentes distribuciones de objetivos en diferentes pliegues. De manera similar, la estratificación también facilita la distribución de objetivos en diferentes pliegues al dividir los datos.

En este proceso, los datos se reorganizan en diferentes pliegues de una manera que asegura que cada pliegue se convierta en un representante del todo. Por lo tanto, si se trata de un problema de clasificación binaria en el que cada clase consta del 50 % de los datos, puede utilizar la estratificación para organizar los datos de manera que cada clase incluya la mitad de las instancias.

El proceso de estratificación es más adecuado para conjuntos de datos pequeños y desequilibrados con clasificación multiclase.

código pitón:

de sklearn.model_selection importar StratifiedKFold

skf = StratifiedKFold(n_splits=5, random_state=Ninguno)

# X es el conjunto de funciones e y es el objetivo

para train_index, test_index en skf.split(X,y):

print(“Tren:”, train_index, “Validación:”, val_index)

X_train, X_test = X[train_index], X[val_index]

y_train, y_test = y[train_index], y[val_index]

Leer: Marcos de datos en Python – Tutorial

¿Cuándo usar cada una de estas cinco estrategias de validación cruzada?

Como mencionamos antes, cada técnica de validación cruzada tiene casos de uso únicos y, por lo tanto, funcionan mejor cuando se aplican correctamente a los escenarios correctos. Por ejemplo, si tiene suficientes datos y es probable que las puntuaciones y los parámetros óptimos (del modelo) para diferentes divisiones sean similares, el enfoque de división de entrenamiento/prueba funcionará de manera excelente.

Sin embargo, si los puntajes y los parámetros óptimos varían para diferentes divisiones, la técnica K-fold será la mejor. Para los casos en los que tiene muy pocos datos, el enfoque LOOCV funciona mejor, mientras que, para conjuntos de datos pequeños y desequilibrados, la estratificación es el camino a seguir.

Esperamos que este artículo detallado lo haya ayudado a obtener una idea detallada de la validación cruzada en Python.

Si tiene curiosidad por aprender sobre ciencia de datos, consulte el Programa ejecutivo PG en ciencia de datos de IIIT-B y upGrad, creado para profesionales que trabajan y ofrece más de 10 estudios de casos y proyectos, talleres prácticos, tutoría con expertos de la industria, 1 -on-1 con mentores de la industria, más de 400 horas de aprendizaje y asistencia laboral con las mejores empresas.