Validação cruzada em Python: tudo o que você precisa saber

Em Data Science, a validação é provavelmente uma das técnicas mais importantes usadas pelos cientistas de dados para validar a estabilidade do modelo de ML e avaliar o quão bem ele seria generalizado para novos dados. A validação garante que o modelo de ML pegue os padrões corretos (relevantes) do conjunto de dados enquanto cancela com êxito o ruído no conjunto de dados. Essencialmente, o objetivo das técnicas de validação é garantir que os modelos de ML tenham um baixo fator de variância de viés.

Hoje vamos discutir detalhadamente uma dessas técnicas de validação de modelo – Validação Cruzada.

O que é validação cruzada?

A validação cruzada é uma técnica de validação projetada para avaliar e avaliar como os resultados da análise estatística (modelo) serão generalizados para um conjunto de dados independente. A validação cruzada é usada principalmente em cenários em que a previsão é o objetivo principal e o usuário deseja estimar o desempenho e a precisão de um modelo preditivo em situações do mundo real.

A validação cruzada busca definir um conjunto de dados testando o modelo na fase de treinamento para ajudar a minimizar problemas como overfitting e underfitting. No entanto, você deve lembrar que tanto a validação quanto o conjunto de treinamento devem ser extraídos da mesma distribuição, caso contrário, isso levaria a problemas na fase de validação.

Aprenda o curso de certificação em ciência de dados das melhores universidades do mundo. Ganhe Programas PG Executivos, Programas de Certificado Avançado ou Programas de Mestrado para acelerar sua carreira.

Benefícios da validação cruzada

• Ajuda a avaliar a qualidade do seu modelo.
• Ajuda a reduzir/evitar problemas de overfitting e underfitting.
• Ele permite selecionar o modelo que fornecerá o melhor desempenho em dados não vistos.

Leia: Projetos Python para Iniciantes

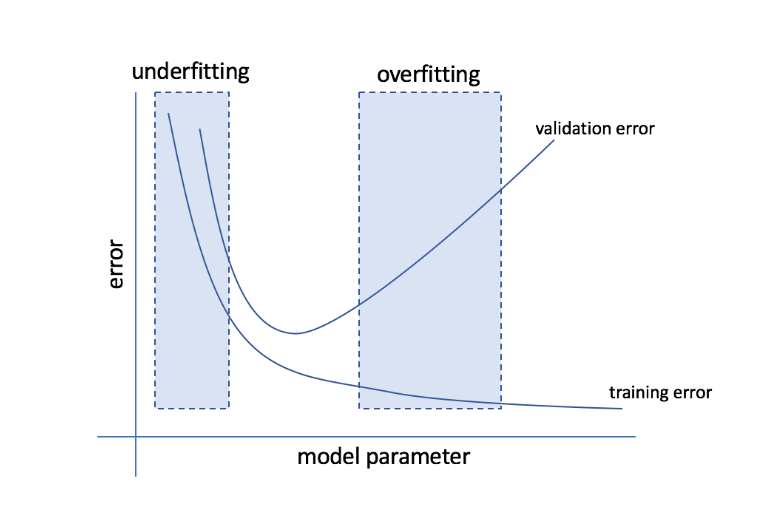
O que são Overfitting e Underfitting?

Overfitting refere-se à condição em que um modelo se torna muito sensível aos dados e acaba capturando muito ruído e padrões aleatórios que não se generalizam bem para dados não vistos. Embora esse modelo geralmente tenha um bom desempenho no conjunto de treinamento, seu desempenho é prejudicado no conjunto de teste.

Underfitting refere-se ao problema quando o modelo falha em capturar padrões suficientes no conjunto de dados, resultando em um desempenho ruim tanto para o treinamento quanto para o conjunto de teste.

Passando por essas duas extremidades, o modelo perfeito é aquele que funciona igualmente bem para conjuntos de treinamento e teste.

Fonte

Validação cruzada: diferentes estratégias de validação

As estratégias de validação são categorizadas com base no número de divisões feitas em um conjunto de dados. Agora, vamos ver as diferentes estratégias de validação cruzada em Python.

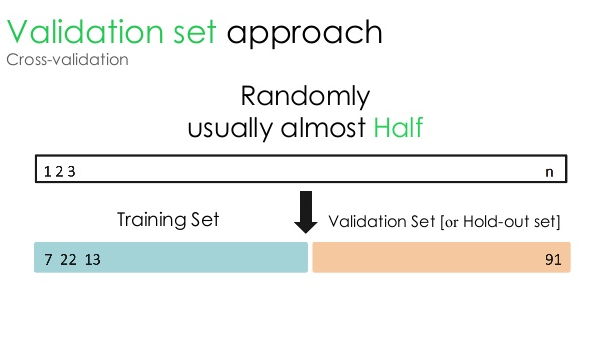
1. Conjunto de validação

Essa abordagem de validação divide o conjunto de dados em duas partes iguais – enquanto 50% do conjunto de dados é reservado para validação, os 50% restantes são reservados para treinamento do modelo. Como essa abordagem treina o modelo com base em apenas 50% de um determinado conjunto de dados, sempre existe a possibilidade de perder informações relevantes e significativas ocultas nos outros 50% dos dados. Como resultado, essa abordagem geralmente cria um viés maior no modelo.

Fonte

Código Python:

treinar, validação = train_test_split(data, test_size=0,50, random_state = 5)

2. Divisão de treinamento/teste

Nesta abordagem de validação, o conjunto de dados é dividido em duas partes – conjunto de treinamento e conjunto de teste. Isso é feito para evitar qualquer sobreposição entre o conjunto de treinamento e o conjunto de teste (se os conjuntos de treinamento e teste se sobrepuserem, o modelo estará com defeito). Assim, é crucial garantir que o conjunto de dados usado para o modelo não contenha amostras duplicadas em nosso conjunto de dados. A estratégia de divisão de treinamento/teste permite treinar novamente seu modelo com base em todo o conjunto de dados sem alterar nenhum hiperparâmetro do modelo.

Fonte

No entanto, essa abordagem tem uma limitação significativa – o desempenho e a precisão do modelo dependem em grande parte de como ele é dividido. Por exemplo, se a divisão não for aleatória, ou se um subconjunto do conjunto de dados tiver apenas uma parte da informação completa, isso levará ao overfitting. Com essa abordagem, você não pode ter certeza de quais pontos de dados estarão em qual conjunto de validação, criando resultados diferentes para conjuntos diferentes. Portanto, a estratégia de divisão de treinamento/teste só deve ser usada quando você tiver dados suficientes em mãos.

Código Python:

>>> de sklearn.model_selection importar train_test_split

>>> X, y = np.arange(10).reshape((5, 2)), range(5)

>>> X

array([[0, 1],

[2, 3],

[4, 5],

[6, 7],

[8, 9]])

>>> lista(s)

[0, 1, 2, 3, 4]

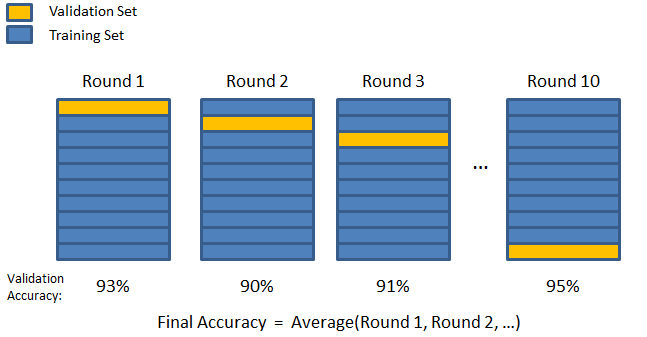
3. Dobra K

Como visto nas duas estratégias anteriores, existe a possibilidade de perder informações importantes no conjunto de dados, o que aumenta a probabilidade de erro induzido por viés ou overfitting. Isso exige um método que reserve dados abundantes para treinamento do modelo e, ao mesmo tempo, deixe dados suficientes para validação.

Insira a técnica de validação K-fold. Nesta estratégia, o conjunto de dados é dividido em número 'k' de subconjuntos ou dobras, em que k-1 subconjuntos são reservados para treinamento do modelo e o último subconjunto é usado para validação (conjunto de teste). O modelo é calculado em relação às dobras individuais e, em seguida, finalizado. Depois que o modelo estiver finalizado, você poderá testá-lo usando o conjunto de teste.

Fonte

Aqui, cada ponto de dados aparece no conjunto de validação exatamente uma vez enquanto permanece no conjunto de treinamento um número k-1 de vezes. Como a maioria dos dados é usada para ajuste, o problema de subajuste reduz significativamente. Da mesma forma, o problema de overfitting é eliminado, pois a maioria dos dados também é usada no conjunto de validação.

Leia: Python vs Ruby: comparação completa lado a lado

A estratégia K-fold é melhor para instâncias em que você tem uma quantidade limitada de dados e há uma diferença substancial na qualidade das dobras ou diferentes parâmetros ideais entre elas.

Código Python:

from sklearn.model_selection import KFold # import KFold

X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]]) # cria um array

y = np.array([1, 2, 3, 4]) # Cria outro array

kf = KFold(n_splits=2) # Define a divisão – em 2 dobras

kf.get_n_splits(X) # retorna o número de iterações de divisão no validador cruzado

imprimir(kf)

KFold(n_splits=2, random_state=Nenhum, shuffle=Falso)

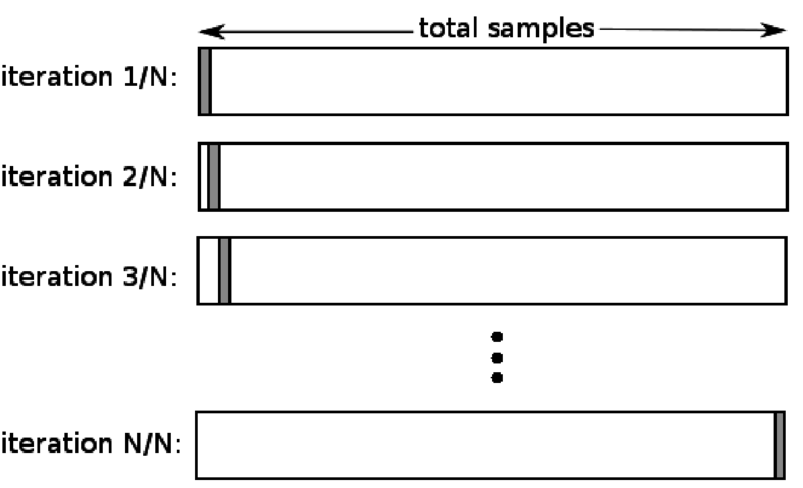
4. Deixe um de fora

A validação cruzada leave one out (LOOCV) é um caso especial de K-fold quando k é igual ao número de amostras em um determinado conjunto de dados. Aqui, apenas um ponto de dados é reservado para o conjunto de teste e o restante do conjunto de dados é o conjunto de treinamento. Portanto, se você usar o objeto “k-1” como amostras de treinamento e o objeto “1” como conjunto de teste, eles continuarão a iterar em cada amostra no conjunto de dados. É o método mais útil quando há poucos dados disponíveis.

Fonte

Como essa abordagem usa todos os pontos de dados, o viés geralmente é baixo. No entanto, como o processo de validação é repetido 'n' vezes (n=número de pontos de dados), leva a um maior tempo de execução. Outra restrição notável dos métodos é que pode levar a uma variação maior na eficácia do modelo de teste à medida que você testa o modelo em relação a um ponto de dados. Portanto, se esse ponto de dados for um valor discrepante, ele criará um quociente de variação mais alto.

Código Python:

>>> importar numpy como np

>>> de sklearn.model_selection importe LeaveOneOut

>>> X = np.array([[1, 2], [3, 4]])

>>> y = np.array([1, 2])

>>> loo = LeaveOneOut()

>>> loo.get_n_splits(X)

2

>>> imprimir(loo)

LeaveOneOut()

>>> para train_index, test_index em loo.split(X):

… print(“TRAIN:”, train_index, “TEST:”, test_index)

… X_train, X_test = X[train_index], X[test_index]

… y_train, y_test = y[train_index], y[test_index]

… print(X_train, X_test, y_train, y_test)

TREM: [1] TESTE: [0]

[[3 4]] [[1 2]] [2] [1]

TREM: [0] TESTE: [1]

[[1 2]] [[3 4]] [1] [2]

5. Estratificação

Normalmente, para a divisão de treinamento/teste e a dobra K, os dados são embaralhados para criar uma divisão aleatória de treinamento e validação. Assim, permite uma distribuição diferente de alvos em diferentes dobras. Da mesma forma, a estratificação também facilita a distribuição de alvos em diferentes dobras enquanto divide os dados.

Nesse processo, os dados são reorganizados em diferentes dobras de forma a garantir que cada dobra se torne um representante do todo. Portanto, se você estiver lidando com um problema de classificação binária em que cada classe consiste em 50% dos dados, poderá usar a estratificação para organizar os dados de forma que cada classe inclua metade das instâncias.

O processo de estratificação é mais adequado para conjuntos de dados pequenos e desbalanceados com classificação multiclasse.

Código Python:

de sklearn.model_selection importar StratifiedKFold

skf = StratifiedKFold(n_splits=5, random_state=Nenhum)

# X é o conjunto de recursos e y é o destino

para train_index, test_index em skf.split(X,y):

print("Trem:", train_index, "Validação:", val_index)

X_train, X_test = X[train_index], X[val_index]

y_train, y_test = y[train_index], y[val_index]

Leia: Data Frames em Python – Tutorial

Quando usar cada uma dessas cinco estratégias de validação cruzada?

Como mencionamos anteriormente, cada técnica de validação cruzada tem casos de uso exclusivos e, portanto, eles têm melhor desempenho quando aplicados corretamente nos cenários certos. Por exemplo, se você tiver dados suficientes e as pontuações e os parâmetros ideais (do modelo) para diferentes divisões provavelmente forem semelhantes, a abordagem de divisão de treinamento/teste funcionará de maneira excelente.

No entanto, se as pontuações e os parâmetros ideais variarem para diferentes divisões, a técnica K-fold será a melhor. Para instâncias em que você tem poucos dados, a abordagem LOOCV funciona melhor, enquanto, para conjuntos de dados pequenos e desequilibrados, a estratificação é o caminho a seguir.

Esperamos que este artigo detalhado tenha ajudado você a obter uma ideia aprofundada de validação cruzada em Python.

Se você está curioso para aprender sobre ciência de dados, confira o Programa PG Executivo em Ciência de Dados do IIIT-B & upGrad, que é criado para profissionais que trabalham e oferece mais de 10 estudos de caso e projetos, workshops práticos práticos, orientação com especialistas do setor, 1 -on-1 com mentores do setor, mais de 400 horas de aprendizado e assistência de trabalho com as principais empresas.