Validation croisée en Python : tout ce que vous devez savoir sur

En science des données, la validation est probablement l'une des techniques les plus importantes utilisées par les scientifiques des données pour valider la stabilité du modèle ML et évaluer dans quelle mesure il se généraliserait à de nouvelles données. La validation garantit que le modèle ML récupère les bons modèles (pertinents) de l'ensemble de données tout en annulant avec succès le bruit dans l'ensemble de données. Essentiellement, l'objectif des techniques de validation est de s'assurer que les modèles ML ont un faible facteur biais-variance.

Aujourd'hui, nous allons discuter longuement d'une telle technique de validation de modèle - la validation croisée.

Qu'est-ce que la validation croisée ?

La validation croisée est une technique de validation conçue pour évaluer et évaluer comment les résultats de l'analyse statistique (modèle) se généraliseront à un ensemble de données indépendant. La validation croisée est principalement utilisée dans les scénarios où la prédiction est l'objectif principal et où l'utilisateur souhaite estimer la qualité et la précision d'un modèle prédictif dans des situations réelles.

La validation croisée cherche à définir un ensemble de données en testant le modèle dans la phase de formation pour aider à minimiser les problèmes tels que le surajustement et le sous-ajustement. Cependant, vous devez vous rappeler que la validation et l'ensemble d'apprentissage doivent être extraits de la même distribution, sinon cela entraînerait des problèmes lors de la phase de validation.

Apprenez le cours de certification en science des données des meilleures universités du monde. Gagnez des programmes Executive PG, des programmes de certificat avancés ou des programmes de maîtrise pour accélérer votre carrière.

Avantages de la validation croisée

• Il permet d'évaluer la qualité de votre modèle.
• Il aide à réduire/éviter les problèmes de surajustement et de sous-ajustement.
• Il vous permet de sélectionner le modèle qui offrira les meilleures performances sur des données invisibles.

Lire : Projets Python pour les débutants

Que sont le surajustement et le sous-ajustement ?

Le surajustement fait référence à la condition dans laquelle un modèle devient trop sensible aux données et finit par capturer beaucoup de bruit et de modèles aléatoires qui ne se généralisent pas bien aux données invisibles. Alors qu'un tel modèle fonctionne généralement bien sur l'ensemble d'apprentissage, ses performances en souffrent sur l'ensemble de test.

Le sous-ajustement fait référence au problème lorsque le modèle ne parvient pas à capturer suffisamment de modèles dans l'ensemble de données, offrant ainsi une mauvaise performance à la fois pour la formation et l'ensemble de test.

En passant par ces deux extrémités, le modèle parfait est celui qui fonctionne aussi bien pour les ensembles d'entraînement que de test.

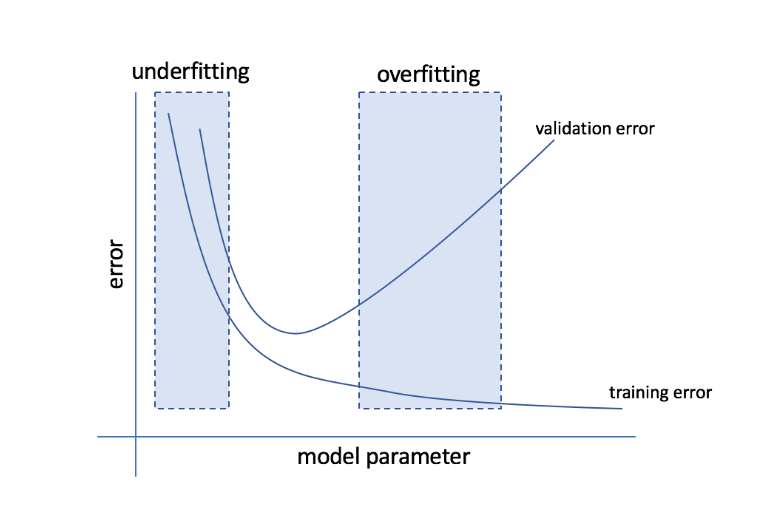
La source

Validation croisée : différentes stratégies de validation

Les stratégies de validation sont classées en fonction du nombre de fractionnements effectués dans un ensemble de données. Examinons maintenant les différentes stratégies de validation croisée en Python.

1. Ensemble de validation

Cette approche de validation divise l'ensemble de données en deux parties égales - tandis que 50 % de l'ensemble de données est réservé à la validation, les 50 % restants sont réservés à la formation du modèle. Étant donné que cette approche forme le modèle sur la base de seulement 50 % d'un ensemble de données donné, il reste toujours une possibilité de manquer des informations pertinentes et significatives cachées dans les 50 % restants des données. Par conséquent, cette approche crée généralement un biais plus élevé dans le modèle.

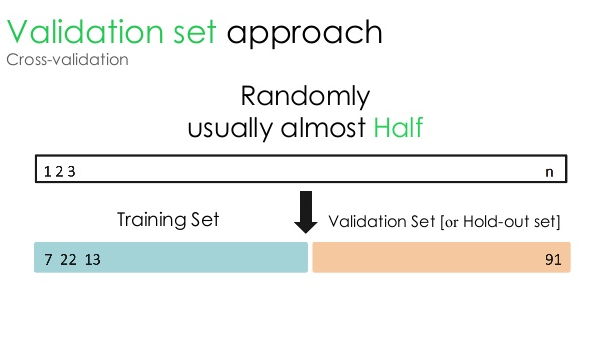
La source

Code Python :

train, validation = train_test_split(data, test_size=0.50, random_state = 5)

2. Répartition entraînement/test

Dans cette approche de validation, l'ensemble de données est divisé en deux parties - l'ensemble d'apprentissage et l'ensemble de test. Ceci est fait pour éviter tout chevauchement entre l'ensemble d'apprentissage et l'ensemble de test (si les ensembles d'apprentissage et de test se chevauchent, le modèle sera défectueux). Ainsi, il est crucial de s'assurer que l'ensemble de données utilisé pour le modèle ne doit pas contenir d'échantillons en double dans notre ensemble de données. La stratégie fractionnée d'entraînement/test vous permet de recycler votre modèle en fonction de l'ensemble de données sans modifier les hyperparamètres du modèle.

La source

Cependant, cette approche a une limite importante - les performances et la précision du modèle dépendent largement de la façon dont il est divisé. Par exemple, si la répartition n'est pas aléatoire ou si un sous-ensemble de l'ensemble de données ne contient qu'une partie des informations complètes, cela entraînera un surajustement. Avec cette approche, vous ne pouvez pas être sûr quels points de données seront dans quel ensemble de validation, créant ainsi des résultats différents pour différents ensembles. Par conséquent, la stratégie fractionnée train/test ne doit être utilisée que lorsque vous disposez de suffisamment de données.

Code Python :

>>> depuis sklearn.model_selection importer train_test_split

>>> X, y = np.arange(10).reshape((5, 2)), range(5)

>>> X

tableau([[0, 1],

[2, 3],

[4, 5],

[6, 7],

[8, 9]])

>>> liste(y)

[0, 1, 2, 3, 4]

3. Pliage en K

Comme on l'a vu dans les deux stratégies précédentes, il est possible de manquer des informations importantes dans l'ensemble de données, ce qui augmente la probabilité d'erreur ou de surajustement induit par un biais. Cela nécessite une méthode qui réserve des données abondantes pour la formation du modèle tout en laissant suffisamment de données pour la validation.

Entrez la technique de validation K-fold. Dans cette stratégie, l'ensemble de données est divisé en un nombre « k » de sous-ensembles ou de plis, où k-1 sous-ensembles sont réservés à la formation du modèle, et le dernier sous-ensemble est utilisé pour la validation (ensemble de test). Le modèle est moyenné par rapport aux plis individuels, puis finalisé. Une fois le modèle finalisé, vous pouvez le tester à l'aide de l'ensemble de test.

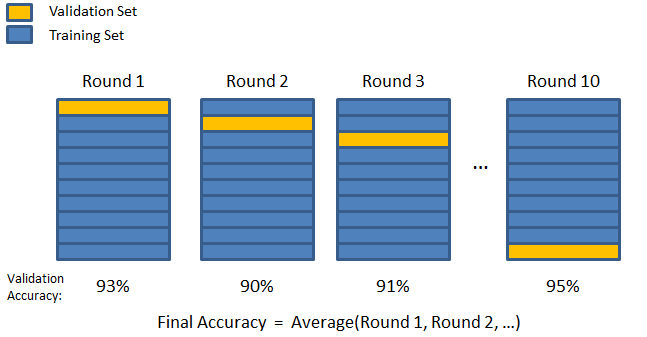
La source

Ici, chaque point de données apparaît dans l'ensemble de validation exactement une fois tout en restant dans l'ensemble d'apprentissage k-1 fois. Étant donné que la plupart des données sont utilisées pour l'ajustement, le problème de sous-ajustement est considérablement réduit. De même, le problème de surajustement est éliminé puisqu'une majorité de données est également utilisée dans l'ensemble de validation.

Lis : Python vs Ruby : comparaison complète côte à côte

La stratégie K-fold est la meilleure pour les cas où vous avez une quantité limitée de données, et il y a une différence substantielle dans la qualité des plis ou différents paramètres optimaux entre eux.

Code Python :

from sklearn.model_selection import KFold # import KFold

X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]]) # crée un tableau

y = np.array([1, 2, 3, 4]) # Créer un autre tableau

kf = KFold(n_splits=2) # Définir le split – en 2 plis

kf.get_n_splits(X) # renvoie le nombre d'itérations de fractionnement dans le validateur croisé

imprimer (kf)

KFold(n_splits=2, random_state=Aucun, shuffle=Faux)

4. Laissez-en un

La validation croisée sans omission (LOOCV) est un cas particulier de K-fold lorsque k est égal au nombre d'échantillons dans un ensemble de données particulier. Ici, un seul point de données est réservé pour l'ensemble de test, et le reste de l'ensemble de données est l'ensemble d'apprentissage. Ainsi, si vous utilisez l'objet "k-1" comme échantillons d'apprentissage et l'objet "1" comme ensemble de test, ils continueront à parcourir chaque échantillon de l'ensemble de données. C'est la méthode la plus utile lorsqu'il y a trop peu de données disponibles.

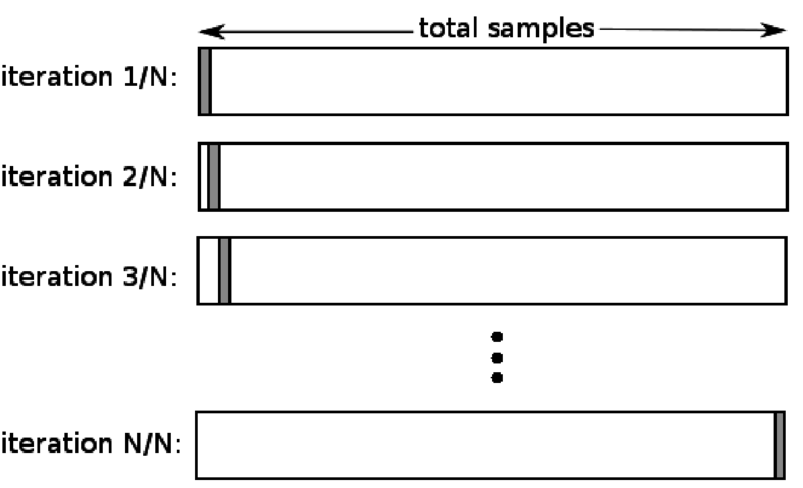
La source

Étant donné que cette approche utilise tous les points de données, le biais est généralement faible. Cependant, comme le processus de validation est répété "n" fois (n = nombre de points de données), cela conduit à un temps d'exécution plus long. Une autre contrainte notable des méthodes est qu'elle peut entraîner une plus grande variation dans l'efficacité du modèle de test lorsque vous testez le modèle par rapport à un point de données. Ainsi, si ce point de données est une valeur aberrante, cela créera un quotient de variation plus élevé.

Code Python :

>>> importer numpy comme np

>>> depuis sklearn.model_selection importer LeaveOneOut

>>> X = np.tableau([[1, 2], [3, 4]])

>>> y = np.tableau([1, 2])

>>> loo = LeaveOneOut()

>>> loo.get_n_splits(X)

2

>>> imprimer (loo)

LeaveOneOut()

>>> pour train_index, test_index dans loo.split(X) :

… print("TRAIN :", index_train, "TEST :", index_test)

… X_train, X_test = X[train_index], X[test_index]

… y_train, y_test = y[train_index], y[test_index]

… print(X_train, X_test, y_train, y_test)

ENTRAÎNER : [1] ESSAI : [0]

[[3 4]] [[1 2]] [2] [1]

ENTRAÎNER : [0] ESSAI : [1]

[[1 2]] [[3 4]] [1] [2]

5. Stratification

En règle générale, pour la répartition entraînement/test et le pli en K, les données sont mélangées pour créer une répartition aléatoire d'apprentissage et de validation. Ainsi, il permet une distribution cible différente dans différents plis. De même, la stratification facilite également la distribution cible sur différents plis tout en divisant les données.

Dans ce processus, les données sont réarrangées dans différents plis de manière à garantir que chaque pli devienne un représentant de l'ensemble. Ainsi, si vous avez affaire à un problème de classification binaire où chaque classe se compose de 50 % des données, vous pouvez utiliser la stratification pour organiser les données de manière à ce que chaque classe comprenne la moitié des instances.

Le processus de stratification est le mieux adapté aux ensembles de données petits et déséquilibrés avec une classification multiclasse.

Code Python :

à partir de sklearn.model_selection importer StratifiedKFold

skf = StratifiedKFold(n_splits=5, random_state=None)

# X est l'ensemble de fonctionnalités et y est la cible

pour train_index, test_index dans skf.split(X,y):

print("Train :", index_train, "Validation :", index_val)

X_train, X_test = X[train_index], X[val_index]

y_train, y_test = y[train_index], y[val_index]

Lire : Data Frames en Python – Tutoriel

Quand utiliser chacune de ces cinq stratégies de validation croisée ?

Comme nous l'avons mentionné précédemment, chaque technique de validation croisée a des cas d'utilisation uniques et, par conséquent, elles fonctionnent mieux lorsqu'elles sont appliquées correctement aux bons scénarios. Par exemple, si vous disposez de suffisamment de données et que les scores et les paramètres optimaux (du modèle) pour différentes divisions sont susceptibles d'être similaires, l'approche de formation/test de division fonctionnera parfaitement.

Cependant, si les scores et les paramètres optimaux varient pour différents fractionnements, la technique du pli en K sera la meilleure. Pour les cas où vous avez trop peu de données, l'approche LOOCV fonctionne mieux, alors que, pour les ensembles de données petits et déséquilibrés, la stratification est la voie à suivre.

Nous espérons que cet article détaillé vous a aidé à acquérir une idée approfondie de la validation croisée en Python.

Si vous êtes curieux d'en savoir plus sur la science des données, consultez le programme Executive PG en science des données de IIIT-B & upGrad qui est créé pour les professionnels en activité et propose plus de 10 études de cas et projets, des ateliers pratiques, un mentorat avec des experts de l'industrie, 1 -on-1 avec des mentors de l'industrie, plus de 400 heures d'apprentissage et d'aide à l'emploi avec les meilleures entreprises.