Dostrajanie hiperparametrów losowego lasu: procesy wyjaśnione za pomocą kodowania

Random Forest to algorytm uczenia maszynowego, który wykorzystuje jako podstawę drzewa decyzyjne. Random Forest jest łatwy w użyciu i elastyczny algorytm ML. Ze względu na swoją prostotę i różnorodność znajduje bardzo szerokie zastosowanie. Daje dobre wyniki w wielu zadaniach klasyfikacyjnych, nawet bez zbytniego dostrajania hiperparametrów.

W tym artykule skupimy się głównie na działaniu Losowego Lasu i różnych hiperparametrach, które można kontrolować w celu uzyskania optymalnych wyników. Potrzeba dostrajania hiperparametrów pojawia się, ponieważ każda z danych ma swoją charakterystykę.

Tymi cechami mogą być typy zmiennych, wielkość danych, binarna/wieloklasowa zmienna docelowa, liczba kategorii w zmiennych kategorycznych, odchylenie standardowe danych liczbowych, normalność danych itp. Dlatego dostrojenie modelu pod kątem danych jest konieczne dla maksymalizacja wydajności modelu.

Konstruuj i działaj

Algorytm losowego lasu działa jako duża kolekcja dekorowanych drzew decyzyjnych. Znana jest również jako technika workowania. Bagging należy do kategorii uczenia się zespołowego i opiera się na teorii, że kombinację hałaśliwych i bezstronnych modeli można uśrednić, aby stworzyć model o niskiej wariancji. Pozwól nam zrozumieć, jak zbudowany jest Losowy Las.

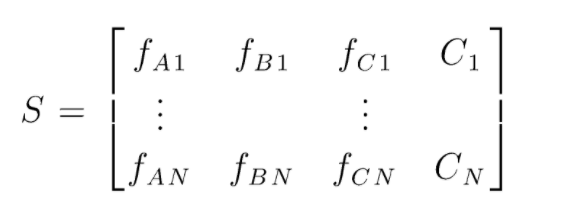
S to macierz danych obecnych do przeprowadzenia losowej klasyfikacji lasów. Istnieje N instancji, a A, B, C to cechy danych. Z tych danych tworzone są losowe podzbiory danych. Nad którymi tworzone są drzewa decyzyjne. Jak widać na poniższym rysunku, na podzbiór danych tworzone jest jedno drzewo decyzyjne, aw zależności od wielkości danych drzewa decyzyjne są również powiększane.

Wynikiem wszystkich wytrenowanych drzew decyzyjnych jest głosowanie, a większość głosowana klasa jest efektywnym wynikiem algorytmu losowego lasu. Modele drzew decyzyjnych przewyższają dane, stąd potrzeba Random Forest. Modele drzew decyzyjnych mogą być modelami Low Bias, ale w większości charakteryzują się wysoką wariancją. Stąd, aby zredukować ten błąd wariancji w zbiorze testowym, stosuje się Random Forest.

Hiperparametry

W losowym lesie można kontrolować różne hiperparametry:

1. N_estymatory: Liczba drzew decyzyjnych budowanych w lesie. Domyślne wartości w sklearn to 100. N_estymatory są w większości skorelowane z rozmiarem danych, aby zawrzeć trendy w danych, potrzebna jest większa liczba DT.
2. Kryterium: Funkcja służąca do mierzenia jakości podziałów w drzewie decyzyjnym (problem klasyfikacji). Obsługiwane kryteria to gini: zanieczyszczenie gini lub entropia: zysk informacji. W przypadku regresji można użyć średniego błędu bezwzględnego (MAE) lub błędu średniokwadratowego (MSE). Domyślnie są to gini i mse.
3. Max_depth: Maksymalne poziomy dozwolone w drzewie decyzyjnym. Jeśli ustawione na nic, drzewo decyzyjne będzie dalej dzielić, aż do osiągnięcia czystości.
4. Max_features: maksymalna liczba funkcji używanych w procesie podziału węzłów. Typy: sqrt, log2. Jeśli łączna liczba funkcji wynosi n_cech, to: sqrt(n_cechy) lub log2(n_cechy) można wybrać jako maksymalną liczbę cech dla podziału węzłów.
5. Bootstrap: Próbki Bootstrap są używane podczas budowania drzew decyzyjnych, jeśli w trybie bootstrap wybrano True, w przeciwnym razie dla każdego drzewa decyzyjnego wykorzystywane są całe dane.
6. Min_samples_split: Ten parametr decyduje o minimalnej liczbie próbek wymaganych do podziału węzła wewnętrznego. Wartość domyślna =2. Problem z tak małą wartością polega na tym, że warunek jest sprawdzany na węźle końcowym. Jeżeli punkty danych w węźle przekraczają wartość 2, następuje dalszy podział. Natomiast jeśli zostanie ustawiona bardziej łagodna wartość, taka jak 6, podział zostanie wcześniej zatrzymany, a drzewo decyzyjne nie będzie się przesadzać z danymi.
7. Min_sample_leaf: Ten parametr określa minimalną liczbę wymagań dotyczących punktów danych w węźle drzewa decyzyjnego. Wpływa na węzeł końcowy i zasadniczo pomaga w kontrolowaniu głębokości drzewa. Jeśli po podziale punkty danych w węźle znajdą się pod liczbą min_sample_leaf, podział nie przejdzie i zostanie zatrzymany w węźle nadrzędnym.

Istnieją inne mniej ważne parametry, które również można wziąć pod uwagę podczas procesu strojenia hiperparametrów.

n_jobs: liczba procesorów, których można użyć do szkolenia. (-1 bez limitu)

max_samples: maksymalna ilość danych, które można wykorzystać w każdym drzewie decyzyjnym

random_state: model z określonym random_state będzie dawał podobną dokładność/wyjścia.

Class_weight: wejście słownikowe, które może obsługiwać niezrównoważone zestawy danych.

Trzeba przeczytać: rodzaje algorytmów AI

Procesy dostrajania hiperparametrów

Istnieją różne sposoby wykonywania procesów dostrajania hiperparametrów. Po utworzeniu i ocenie modelu podstawowego hiperparametry można dostroić, aby zwiększyć niektóre określone metryki, takie jak dokładność lub wynik f1 modelu.

Należy sprawdzić błędy przemieszczenia i wariancji odchylenia przed i po regulacjach. Model należy dostroić zgodnie z wymaganiami czasu rzeczywistego. Czasami przesadny model może być bardzo wrażliwy na fluktuacje danych w walidacji, dlatego wyniki walidacji krzyżowej z odchyleniem walidacji krzyżowej powinny być sprawdzane pod kątem możliwego dopasowania przed i po dostrojeniu modelu.

W dalszej części omówiono metody strojenia Random Forest w Pythonie.

CV z losowym wyszukiwaniem

Możemy użyć scikit learning i RandomisedSearchCV, gdzie możemy zdefiniować siatkę, losowy model lasu będzie dopasowywany w kółko przez losowy wybór parametrów z siatki. Nie uzyskamy najlepszych parametrów, ale na pewno dostaniemy najlepszy model z różnych modeli, które są dopasowywane i testowane.

Kod źródłowy:

ze sklearn.model_selection import GridSearchCV

# Utwórz siatkę wyszukiwania parametrów, które zostaną przetasowane

param_grid = {

'bootstrap': [Prawda],

'max_depth': [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, Brak],

'max_features': ['auto', 'sqrt'],

'min_samples_leaf': [1, 2, 4],

'min_samples_split': [2, 5, 10],

'n_estymatory': [200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000]

}

# Korzystanie z losowej siatki i wyszukiwanie najlepszych hiperparametrów

rf = RandomForestRegressor() #tworzenie modelu bazowego

rf_random = RandomizedSearchCV(estymator = rf, param_distributions = random_grid, n_iter = 100, cv = 5, verbose=2, random_state=42, n_jobs = -1)

rf_random.fit(train_features, train_labels) #fit to zainicjowanie procesu szkoleniowego

Funkcja wyszukiwania losowego przeszuka parametry poprzez 5-krotną walidację krzyżową i 100 iteracji, aby uzyskać najlepsze parametry.

CV wyszukiwania w siatce

Wyszukiwanie siatkowe jest używane po losowym wyszukiwaniu w celu zawężenia zakresu w celu wyszukania idealnych hiperparametrów. Teraz, gdy wiemy, na czym możemy się skoncentrować, możemy jawnie przeprowadzić te parametry przez wyszukiwanie w siatce i ocenić różne modele, aby uzyskać ostateczne wartości dla każdego hiperparametru.

Kod źródłowy:

ze sklearn.model_selection import GridSearchCV

# Utwórz siatkę parametrów na podstawie wyników wyszukiwania losowego

param_grid = {

'bootstrap': [Prawda],

'max_depth': [80, 90, 100, 110],

'max_features': [2, 3],

'min_samples_leaf': [3, 4, 5],

'min_samples_split': [8, 10, 12],

'n_estymatory': [100, 200, 300, 1000]

}

# Stwórz model oparty

rf = RandomForestRegressor()

# Utwórz wystąpienie modelu wyszukiwania siatki

grid_search = GridSearchCV (estymator = rf, param_grid = param_grid,

cv = 3, n_jobs = -1, gadatliwy = 2)

Wyniki po wykonaniu:

# Dopasuj wyszukiwanie siatki do danych

grid_search.fit(train_features, train_labels)

grid_search.best_params_

{'bootstrap': Prawda,

'maks.głębokość': 80,

'max_features': 3,

'min_samples_leaf': 5,

'min_samples_split': 12,

'n_estymatory': 100}

best_grid = grid_search.best_estimator_

Przeczytaj także: Pomysły na projekty uczenia maszynowego

Wniosek

Przeanalizowaliśmy działanie losowego modelu lasu i sposób działania każdego hiperparametru w celu zmiany drzew decyzyjnych, a tym samym losowego modelu lasu jako całości. Przyjrzeliśmy się również wydajnej technice łączenia wykorzystania wyszukiwania losowego i siatki, aby uzyskać najlepsze parametry dla naszego modelu. Dostrajanie hiperparametrów jest bardzo ważne, ponieważ pomaga nam kontrolować działanie odchylenia i wariancji naszego modelu.

Jeśli chcesz dowiedzieć się więcej o drzewie decyzyjnym, uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznych szkoleń, ponad 30 studiów przypadków i zadania, status absolwentów IIIT-B, ponad 5 praktycznych praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.