Analiza wyrażeń w strukturze danych: rodzaje notacji, asocjatywność i pierwszeństwo
Opublikowany: 2020-10-07Parsowanie to proces analizowania ciągu symboli, wyrażonych w językach naturalnych lub komputerowych, które będą zgodne z gramatyką formalną . Analiza wyrażeń w strukturze danych oznacza ocenę wyrażeń arytmetycznych i logicznych. Najpierw zobaczmy, jak napisane jest wyrażenie arytmetyczne:
- 9+9
- Cb
Wyrażenie może być napisane ze stałymi, zmiennymi i symbolami, które mogą pełnić rolę operatora lub nawiasu. Całe to wyrażenie musi przestrzegać określonego zestawu zasad. Zgodnie z tą zasadą parsowanie wyrażenia odbywa się na podstawie gramatyki.
Wyrażenie arytmetyczne wyrażone jest w postaci Notation . Istnieją trzy sposoby na napisanie wyrażenia w arytmetyce:
- Notacja wrostkowa
- Prefiks (polski) Notacja
- Notacja postfiksowa (odwrotna-polska)
Jednak po zapisaniu wyrażenia dane wyjściowe żądanego wyrażenia pozostają takie same. Zanim zaczniemy z typami notacji, zobaczmy, jakie są asocjatywność i pierwszeństwo w analizie wyrażeń w strukturze danych.
Jeśli jesteś początkującym i chcesz dowiedzieć się więcej na temat nauki o danych, sprawdź nasze kursy nauki o danych prowadzone przez najlepsze uniwersytety.
Przeczytaj: Wykresy w strukturze danych
Spis treści
Łączność
Zanim zaczniesz, musisz wiedzieć, czym jest właściwość Asocjatywność; udostępnia zasady zmiany nawiasów w wyrażeniu w celu zapewnienia prawidłowego dowodu. Oznacza to, że rearanżacja nawiasu musi dać taką samą wartość jak równanie rodzicielskie. Zapewnia prawidłową zasadę zastępowania operatorów.
W wyrażeniu zawierającym dwa lub więcej operatorów wykonywana operacja nie ma znaczenia, chyba że sekwencja operandów nie jest wymieniana. Jeśli wyrażenie jest napisane w nawiasach i we wrostku, zmiana pozycji nie zmienia wartości.
Ponieważ w językach indoeuropejskich wyrażenia są czytane od lewej do prawej, większość operatorów wrostkowych jest lewostronnie łączona; operatory są oceniane w tym samym priorytecie. Rosnąca siła jest zasadą stosowaną przy rozważaniu operatorów wrostkowych. Operatory przedrostkowe są zazwyczaj prawostronnie zespolone, a operatory przyrostka lewostronnie zespolone.
W niektórych językach operatory i operandy mają równą wartość, przy czym Asocjatywność nie jest wyraźna. Chociaż w niektórych językach operatory nie są asocjacyjne, to sprawia, że użycie złożonych wyrażeń jest konieczne do użycia nawiasów, co zwiększa złożoność dla programistów.
Pierwszeństwo w strukturze danych
Kolejność pierwszeństwa oznacza kolejność, w jakiej muszą podążać operatory w zestawieniu wyrażeń. Jest to często używane podczas pracy z Infix Notation.
W sytuacji <operator> <operand> <operator> operand pomiędzy dwoma operatorami, preferencja przydzielenia operatora jest dość trudna. Dlatego do obliczeń stosuje się reguły pierwszeństwa operatora. Np. Tutaj mnożenie ma wyższy priorytet, a później wykonywana jest operacja dodawania.
- Najczęstszą, ale nie tak oczywistą zasadą jest to, że operacje mnożenia i dzielenia muszą być wykonane przed dodawaniem i odejmowaniem. Zazwyczaj są one zbierane w ten sam sposób, więc wszyscy operatorzy mają jednakową wagę.
- Biorąc pod uwagę tę operację w formacie logicznym, zmienność jest widoczna w „i” i „lub”. Wiele języków zapewnia równą wagę, w których operacja „lub” ma wyższy priorytet. Niektóre języki uwzględniają mnożenie lub „&”, „&” dodawanie „lub” równą pierwszeństwo, gdzie większość języków zapewnia operacje arytmetyczne z najwyższym pierwszeństwem.
- Przeciążenie jest spowodowane brakiem odpowiedniego przypisania pierwszeństwa. Wiele języków zapewnia negację (prawda/fałsz) wyższą pierwszeństwo niż wyrażenia algebry wektorowej, podczas gdy niektóre zapewniają równą pierwszeństwo.
Przeczytaj także: Pomysły na projekty dotyczące struktury danych
Rodzaje notacji
Teraz nauczmy się, jak pozycja operatora decyduje o rodzaju notacji.
1. Notacja wrostkowa
W notacji Infix operatory są używane pomiędzy operandami. Podczas czytania wyrażenia Infix Notation jest dość łatwy dla ludzi. Ale przetwarzanie argumentu wrostkowego, jeśli chodzi o algorytm komputerowy, zajmuje dość czasu i miejsca. Np.: p + q
<operandy> <operatory> <operandy>
Infix Notation wymaga dodatkowych informacji do wykonania oceny; Reguły są konstruowane w języku wyrażeń za pomocą operatora Asociativity , Na przykład: p * ( q + r ) / s
- Reguły łączności sugerują, że wyrażenie musi być wykonywane od lewej do prawej, tak że mnożenie przez p jest wykonywane przed dzieleniem q.
- Podobnie zasady pierwszeństwa sugerują, że operacja mnożenia i dzielenia jest wykonywana przed wykonaniem operacji dodawania i odejmowania.
2. Notacja przedrostkowa
Tutaj operator jest zapisywany jako pierwszy, a następnie operand. Jest również nazywany notacją polską. Np. +pq
<operatory> <operandy> <operandy>
Np.: p * ( q + r ) / s
Ocena musi być wykonywana od lewej do prawej, a nawiasy nie zmieniają ani nie zmieniają wzoru równania. Tutaj dodawanie musi zostać zakończone przed mnożeniem, ponieważ pozycja „+” jest na lewo od „*”.
Tutaj każdy operator wykonuje operacje na wartościach znajdujących się bezpośrednio po ich lewej stronie. Na przykład „+” powyżej używa „q” i „r”. Możemy zsumować nawiasy, aby to było jawne:
((p (qr +) *) s /)
Tak więc „( )” uwzględnia i wykorzystuje dwie wartości bezpośrednio poprzedzające „p” oraz wynik +. Podobnie, „/” używa wyniku wyrażenia mnożenia i „s”.
3. Notacja postfiksowa
Notacja postfiksowa, głównie operand, jest zapisywana, po której następuje operator. Jest również nazywany odwrotną notacją polską, np. pq+

<operandy> <operandy> <operatory>
Jeśli chodzi o Postfix, tak samo jak operacja Prefix wyrażenia jest od lewej do prawej, a „( )” są niepotrzebne. Tutaj operatory wykonują na dwóch najbliższych wartościach od prawej. W poniższym przykładzie niepotrzebnie dodano nawiasy, aby wyjaśnić, że nie ma to wpływu na ocenę.
(/ (* p (+ qr)) ) s)
Tutaj „ocena operatora jest od lewej do prawej” wartości operacji są po ich prawej stronie, a jeśli same wartości wymagają obliczeń, to następuje zmiana kolejności oceny. W powyższym przykładzie zobaczmy, że „/” jest głównym operatorem po lewej stronie.
Czeka na zakończenie operacji mnożenia. A przede wszystkim operacja mnożenia musi być wykonana przed rozpoczęciem obliczania dzielenia (a z powyższego przykładu jasno wynika, że operacja dodawania musi zostać zakończona przed operacją mnożenia).
Ponieważ operatory Postfix Notation używają wartości po prawej stronie; wszelkie wartości obejmujące obliczenia będą miały już ukończone obliczenia, gdy przejdziemy w lewo. Możemy więc wywnioskować, że obliczanie wyrażenia nie jest takie samo, jak działanie operatora przedrostka.
Aby wyróżnić wszystkie trzy notacje, operandy występują w tej samej kolejności, a operatory należy przesunąć, aby zapewnić właściwe znaczenie podczas obliczeń. Należy to wziąć pod uwagę, szczególnie biorąc pod uwagę operatory asymetryczne „-” i „/”, aby było jasne, że pq jest zawsze qr, chyba że mają tę samą wartość; wartości są równoważne „pq -” lub „- pq”
P+q ≡ +pq ≡ pq+
Np:
Wrostek- p * q + r / s
Prefiks – pq * rs / +
Post fix – + * pq / rs
Najpierw, aby wykonać operację, pomnóż p i q, a następnie podziel r przez s i na koniec dodaj wyniki.
Poniżej tabela figi pomiędzy trzema Notacjami,
| Notacja wrostkowa | Notacja polska | Odwrotna notacja polska |
| p+q | +pq | pq+ |
| (p+q)*r | +*pq | pqr++ |
| p*(q+r) | *p+qr | pqr*+ + |
| p÷q+r÷s | +÷pq÷rs | pq÷rs÷+ |
| (pq)*(rs) | *-pq-rs | pq-rs-* |
Konwersja między notacjami
*Aby zapewnić jasny wgląd, w wyrażeniu dodano nawiasy,
| Infiks | Przyrostek | Prefiks |
| ( (p * q) + (r / s)) | ( (pq *) (rs /) +) | (+ (* pq) (/ rs) ) |
| ((p * (q + r)) ) / s) | ( (p (qr +) *) s /) | (/ (* p (+ qr)) ) s) |
| (p * (q + (r / s)) ) | (p (q (rs /) +) *) | (* p (+ q (/ rs)) ) ) |
- Możesz rozpocząć konwersję bezpośrednio w formach w nawiasach przez operatory w nawiasie, np. (m + n) lub (mn +) lub (+ mn). Teraz powtórz to u wszystkich operatorów, usuwając niechciane wsporniki.
- Teraz użyj tej sztuczki pokazanej powyżej, aby przekonwertować i przeanalizować drzewa – równoważne drzewa analizy dla każdego węzła to:
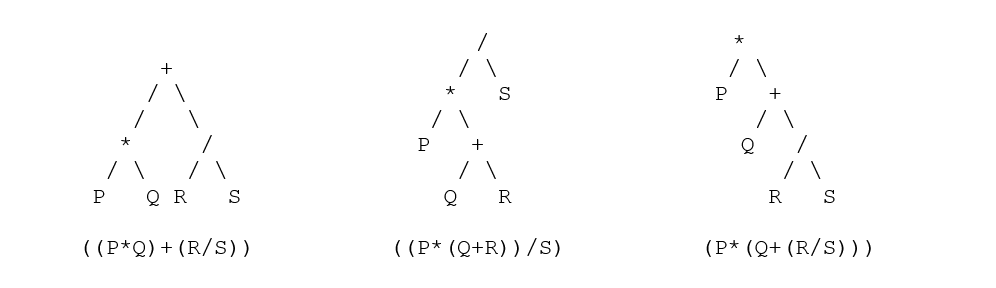
Zamówienie: struktura danych i algorytm w Pythonie
Wniosek
Analiza wyrażeń w strukturach danych , wrostkach, przyrostkach i przedrostkach w wyrażeniach arytmetycznych są zupełnie inne, ale mają te same sposoby pisania wyrażeń. Znajomość tych zagadnień jest niezbędna przy pisaniu programów.
W języku programowania komputerowego wyrażenie jest rozważane i analizowane na podstawie ciągu. Reguła stowarzyszenia i pierwszeństwa dość się zmienia w różnych językach.
Dlaczego warto wybrać kurs Data science z upGrad?
Nauka o danych jest jedną z dynamicznie rozwijających się dziedzin informatyki. Firmy potrzebują programistów, którzy mają dobrą znajomość podstaw, co jest podstawą programowania niezależnie od języka kodowania.
upGrad koncentruje się na zapewnianiu wnikliwych i pouczających zajęć, obejmujących każdą podstawową potrzebę zostania naukowcem danych. 12-miesięczny program Executive PG w dziedzinie nauki o danych. , oferowany przez IIIT Bangalore, to pierwszy w Indiach certyfikowany kurs NASSCOM, który obejmuje spersonalizowaną opiekę mentorską 1:1 od ekspertów z branży Data Science, obejmującą wszystkie niezbędne języki programowania, narzędzia i biblioteki. Zapewnia najlepszą podstawę do rozpoczęcia dobrze płatnej pracy w zakresie analizy danych.
Czym są struktury danych?
Struktury danych służą do organizowania danych w pamięci. Istnieje kilka metod porządkowania danych w pamięci, w tym tablice, listy, stosy, kolejki i wiele innych. Struktura danych nie jest językiem programowania, takim jak C, C++ lub Java. Zamiast tego jest to zestaw technik, które są używane do porządkowania danych w pamięci w dowolnym języku programowania. Struktura danych to metoda wydajnego organizowania, obsługi i przechowywania danych. Elementy danych można po prostu przeszukiwać za pomocą struktury danych. Ma to kluczowe znaczenie dla poprawy szybkości programu, ponieważ głównym zadaniem programu jest zapisywanie i pobieranie danych użytkownika tak szybko, jak to możliwe.
Jakie są rzeczywiste zastosowania analizowania danych?
Proces przekształcania danych z jednego formatu na inny jest znany jako parsowanie danych. Są szeroko stosowane w kompilatorach do analizowania kodu komputerowego i generowania kodu maszynowego. Proces konwersji danych z jednego formatu na inny jest znany jako parsowanie danych. Ponieważ surowy kod HTML, który otrzymujemy, jest trudny do zrozumienia, parsery są często wykorzystywane do scrapingu online. Wymagamy przekonwertowania danych na format czytelny dla człowieka. Może to sugerować tworzenie raportów przy użyciu ciągów lub tabel HTML w celu dostarczenia najbardziej odpowiednich informacji.
W jaki sposób asocjatywność i pierwszeństwo pomagają w strukturyzacji danych?
Kolejność oceny wyrażeń jest określona przez dwie właściwości operatorów: pierwszeństwo i asocjatywność. Pierwszeństwo pomaga w ustaleniu, w jaki sposób terminy w wyrażeniu powinny być grupowane i jak należy oceniać wyrażenie. Ponieważ większość wyrażeń korzysta ze struktury BODMAS, niektóre operatory mają pierwszeństwo przed innymi. Gdy dwa operatory mają ten sam priorytet w wyrażeniu, stosowana jest zasada łączności. Zgodnie z preferencjami kompilatora asocjatywność może być albo od lewej do prawej, albo od prawej do lewej.
