データ構造における式の解析：表記の種類、結合性、優先順位

公開: 2020-10-07

構文解析は、形式文法に一致する自然言語またはコンピューター言語で表現された一連の記号を分析するプロセスです。 データ構造での式の解析とは、算術式と論理式の評価を意味します。 まず、算術式がどのように記述されているかを見てみましょう。

9 + 9
Cb

式は、演算子または括弧として機能できる定数、変数、および記号を使用して記述できます。この式はすべて、特定のルールセットに従う必要があります。この規則に従って、式の構文解析は文法に基づいて行われます。

算術式は、表記法の形式で表されます。 さて、算術で式を書くには3つの方法があります。

中置記法
接頭辞（ポーランド記）表記
後置（逆ポーランド）表記

ただし、式が書き込まれるとき、目的の式の出力は同じままです。表記法の種類を開始する前に、データ構造の式解析で結合性と優先順位がどのようになっているのかを見てみましょう。

初心者でデータサイエンスについて詳しく知りたい場合は、一流大学のデータサイエンスコースをご覧ください。

読む：データ構造のグラフ

連想性

始める前に、結合法則が何であるかを知る必要があります。有効な証明を提供するために、式の括弧を再配置するためのルールを提供します。これは、ブラケットの再配置が親方程式と同じ値を与える必要があることを意味します。演算子を置き換えるための有効なルールを提供します。

2つ以上の演算子を含む式では、オペランドのシーケンスが交換されない限り、実行される操作は重要ではありません。式が角かっこを使用して中置で記述されている場合、位置を変更しても値は変更されません。

インド・ヨーロッパ語族では、式は左から右に読み取られるため、ほとんどの中置演算子は左結合です。演算子は同じ優先順位で評価されます。パワーの上昇は、中置演算子を検討する際に使用されるルールです。接頭辞演算子は一般に右結合であり、接尾演算子は左結合です。

一部の言語では、演算子とオペランドに等しい値が与えられます。この場合、結合性はこの言語シーケンスを明示的にすることとは見なされません。一部の言語では、演算子は関連付けられていませんが、これにより、角かっこを使用するために必要な複雑な式が使用されるため、プログラマーの複雑さが増します。

データ構造の優先順位

優先順位とは、式のステートメントで演算子が従う必要のある順序を意味します。これは、中置記法を使用するときに一般的に使用されます。

2つの演算子の間に<operator> <operand><operator>オペランドがある状況では、演算子を割り当てる設定は非常に注意が必要です。 したがって、計算には演算子の優先順位規則に従います。たとえば、ここでは乗算の優先順位が高く、後で加算演算が実行されます。

最も一般的ですが、それほど明白ではない規則は、加算と減算の前に乗算と除算の演算を実行する必要があるということです。通常、これらは同じ方法で収集されるため、すべてのオペレーターに同等の重要性が提供されます。
この操作を論理形式で考えると、「and」と「or」に変化が見られます。多くの言語は同等の重要性を提供し、「または」操作にはより高い優先順位が与えられます。一部の言語では、乗算または「＆」、「＆」加算「または」が等しい優先順位と見なされます。ほとんどの言語では、最高の優先順位で算術演算が提供されます。
優先順位が適切に割り当てられていないために、オーバーロードが発生します。多くの言語は、ベクトル代数式よりも高い優先順位（true / false）を提供しますが、同等の優先順位を提供する言語もあります。

また読む：データ構造プロジェクトのアイデア

表記の種類

次に、オペレーターの位置が表記のタイプを決定する方法を学びましょう。

1.中置記法

中置記法では、オペランドの間に演算子が使用されます。式を読んでいる間、中置記法は人間にとって非常に簡単です。しかし、コンピューターアルゴリズムに関しては、中置引数を処理するのにかなりの時間とスペースがかかります。例：p + q

<オペランド> <演算子> <オペランド>

中置記法では、評価を実行するために追加情報が必要です。ルールは、演算子の結合性、例：p *（q + r）/ s

結合法則は、式を左から右に実行する必要があることを示唆しています。これにより、pによる乗算はqの除算の前に実行されます。
同様に、優先順位の規則では、加算と減算の演算を実行する前に、乗算と除算の演算を実行することを推奨しています。

2.プレフィックス表記

ここでは、演算子が最初に記述され、次にオペランドが記述されます。ポーランド記法とも呼ばれます。例+pq

<演算子> <オペランド><オペランド>

例：p *（q + r）/ s

評価は左から右に実行する必要があり、括弧は方程式のパターンを変更または変更しません。ここでは、「*」の左側に「+」の位置があるため、乗算の前に加算を完了する必要があります。

ここで、すべての演算子は、それらのすぐ左にある値に対して操作を実行します。たとえば、上記の「+」は「q」と「r」を使用します。角かっこを合計して、これを明白にすることができます。

（（p（qr +）*）s /）

したがって、「（）」は、「p」の直前の2つの値と、+の結果を考慮して使用します。同様に、「/」は乗算式と「s」の結果を使用します。

3.後置表記

後置記法、主にオペランドが記述され、その後に演算子が続きます。逆ポーランド記法とも呼ばれます。例：pq +

<オペランド><オペランド> <演算子>
Postfixは、式のPrefix操作と同じように左から右になり、「（）」は不要です。ここで、演算子は右から最も近い2つの値に対して実行します。以下の例では、評価に影響がないことを明確にするために、括弧が不必要に追加されています。
（/（* p（+ qr））s）
ここで、「演算子の評価は左から右へ」の操作値は右側にあり、値自体に計算が含まれる場合は、評価の順序が変更されます。上記の例を見ると、左側の「/」が主要な演算子であることがわかります。

乗算演算が完了するまで待機します。そして、主に、除算の計算を開始する前に乗算演算を実行する必要があります（上記の例から、乗算演算の前に加算演算を完了する必要があることは明らかです）。
Postfix Notation演算子は、その右側の値を使用するためです。計算を含む値は、左に移動するときにすでに計算が完了しています。したがって、式の計算はプレフィックス演算子の操作と同じではないと結論付けることができます。
3つの表記法すべてを強調表示するには、オペランドの順序が同じであり、計算中に正しい意味を提供するために演算子を移動する必要があります。これは、非対称演算子「-」と「/」を検討する場合に特に考慮する必要があります。これにより、pqが同じ値でない限り、常にqrであることが明確になります。値は「pq-」または「-pq」と同等です。

P+q≡+pq≡pq+
例えば：
中置-p*q + r / s
プレフィックス– pq * rs / +
修正後– + * pq / rs
まず、演算を実行するには、pとqを乗算し、後でrをsで除算し、最後に結果を加算します。
以下の3つの表記法の概要は次のとおりです。
中置記法 ポーランド記法 逆ポーランド記法
p + q + pq pq +
（p + q）* r + * pq pqr + *
p *（q + r） * p + qr pqr * + +
p÷q+r÷s +÷pq÷rs pq÷rs÷+
（pq）*（rs） *-pq-rs pq-rs- *
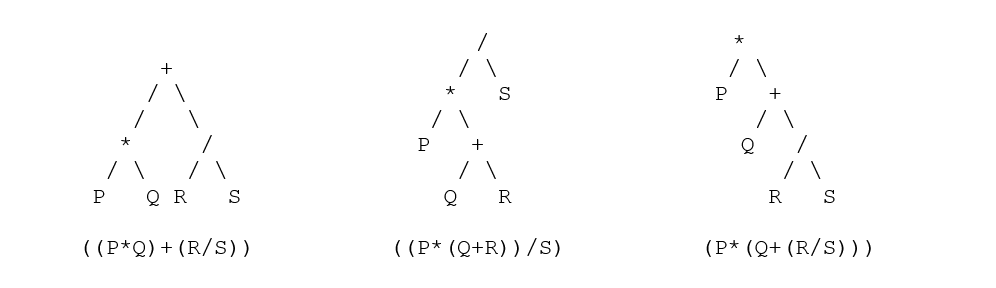
表記間の変換
*明確な洞察を提供するために、式に角かっこが追加されています。

中置 Postfix プレフィックス
（（p * q）+（r / s））（（pq *）（rs /）+）（+（* pq）（/ rs））
（（p *（q + r））/ s）（（p（qr +）*）s /）（/（* p（+ qr））s）
（p *（q +（r / s）））（p（q（rs /）+）*）（* p（+ q（/ rs）））
（m + n）、（mn +）、（+ mn）など、括弧内の演算子を使用して、括弧付きの形式で直接変換を開始できます。次に、不要なブラケットを削除して、すべてのオペレーターでこれを繰り返します。
次に、上記のトリックを使用して、ツリーを変換および解析します。各ノードの同等の解析ツリーは次のとおりです。

チェックアウト： Pythonのデータ構造とアルゴリズム
結論
データ構造での式の解析、算術式でのInfix、Postfix、およびPrefix表記はまったく異なりますが、式の記述方法は同じです。 これらの知識は、プログラムを作成する上で不可欠です。
コンピュータプログラミング言語では、式は文字列から考慮され、解析されます。結合性と優先順位の規則は、言語によって大きく異なります。
なぜupGradでデータサイエンスコースを選ぶのですか？
データサイエンスは、コンピュータサイエンスの急成長分野の1つです。企業には、コーディング言語に関係なくプログラミングの基礎となる基本的な知識を持ったプログラマーが必要です。
upGradは、データサイエンティストになるためのすべての基本的なニーズをカバーする、洞察に満ちた有益なクラスの提供に重点を置いています。 upGradのデータサイエンスにおける12か月のエグゼクティブPGプログラム。 IIITバンガロールが提供するは、インドで最初のNASSCOM認定コースであり、データサイエンス業界の専門家による1対1の個別指導が含まれ、すべての重要なプログラミング言語、ツール、ライブラリをカバーしています。これは、高額のデータサイエンスの仕事を始めるための最良の基盤を提供します。
データ構造とは何ですか？
データ構造は、メモリ内のデータを整理するために使用されます。配列、リスト、スタック、キューなど、メモリ内のデータを配置する方法はいくつかあります。データ構造は、C、C ++、またはJavaのようなプログラミング言語ではありません。代わりに、任意のプログラミング言語でメモリ内のデータを配置するために使用されている一連の手法です。データ構造は、データを効率的に整理、処理、および保存する方法です。データ項目は、データ構造の助けを借りて簡単にトラバースすることができます。プログラムの主な仕事はユーザーのデータを可能な限り迅速に保存および取得することであるため、プログラムの速度を向上させる上で非常に重要です。
データ解析の実際の使用法は何ですか？
データをある形式から別の形式に変換するプロセスは、データ解析と呼ばれます。これらは、コンピューターコードを解析し、マシンコードを生成するためにコンパイラーで広く使用されています。データをある形式から別の形式に変換するプロセスは、データ解析と呼ばれます。私たちが受け取る生のHTMLは理解しにくいため、パーサーはオンラインスクレイピングでよく使用されます。データを人間が読める形式に変換する必要があります。これは、最も関連性の高い情報を提供するためにHTML文字列またはテーブルを使用してレポートを作成することを意味する場合があります。
結合性と優先順位はデータ構造化にどのように役立ちますか？
式の評価順序は、演算子の2つのプロパティ（優先順位と結合性）によって決定されます。優先順位は、式の用語をグループ化する方法と、式を評価する方法を確立するのに役立ちます。ほとんどの式はBODMASフレームワークを使用するため、特定の演算子が他の演算子よりも優先されます。式で2つの演算子の優先順位が同じである場合、結合法則が適用されます。コンパイラの好みに応じて、結合性は左から右または右から左のいずれかになります。