Aprendizaje automático bayesiano: exploración de un cambio de paradigma en el modelado de datos estadísticos
Publicado: 2020-11-24Tabla de contenido
¿Qué es el aprendizaje automático bayesiano?
El aprendizaje automático bayesiano (también conocido como aprendizaje automático bayesiano) es un enfoque sistemático para construir modelos estadísticos, basado en el teorema de Bayes.
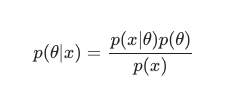Cualquier problema estándar de aprendizaje automático incluye dos conjuntos de datos principales que necesitan análisis:
- Un conjunto completo de datos de entrenamiento
- Una colección de todas las entradas disponibles y todas las salidas registradas
El enfoque tradicional para analizar estos datos para el modelado es determinar algunos patrones que se pueden mapear entre estos conjuntos de datos. Un analista generalmente empalmará un modelo para determinar el mapeo entre estos, y el enfoque resultante es un método muy determinista para generar predicciones para una variable objetivo.
El único problema es que no hay absolutamente ninguna forma de explicar lo que sucede dentro de este modelo con un conjunto claro de definiciones. Todo lo que se logra, esencialmente, es la minimización de algunas funciones de pérdida en el conjunto de datos de entrenamiento, pero eso difícilmente califica como un verdadero modelado.
Un modelo ideal (y preferiblemente, sin pérdidas) implica un resumen objetivo de los parámetros inherentes del modelo, complementado con huevos de pascua estadísticos (como intervalos de confianza) que se pueden definir y defender en el lenguaje de la probabilidad matemática. Este escenario "ideal" es lo que el aprendizaje automático bayesiano se propone lograr.
Los objetivos (y la magia) del aprendizaje automático bayesiano
El objetivo principal del aprendizaje automático bayesiano es estimar la distribución posterior , dada la probabilidad (una estimación derivada de los datos de entrenamiento) y la distribución previa .
Cuando entrenamos un modelo regular de aprendizaje automático, esto es exactamente lo que terminamos haciendo en la teoría y la práctica. Se sabe que los analistas realizan iteraciones sucesivas de Estimación de máxima verosimilitud en los datos de entrenamiento, actualizando así los parámetros del modelo de una manera que maximiza la probabilidad de ver los Conduce a un problema del huevo y la gallina, que el aprendizaje automático bayesiano pretende resolver maravillosamente.
Las cosas toman un giro completamente diferente en un caso dado donde un analista busca maximizar la distribución posterior , asumiendo que los datos de entrenamiento son fijos y, por lo tanto, determinando la probabilidad de cualquier configuración de parámetro que acompañe a dichos datos. Este proceso se llama Máximo A Posterior , abreviado como MAP . Una forma más fácil de comprender este concepto es pensar en él en términos de la función de probabilidad .
Teniendo en cuenta el Teorema de Bayes , la posterior se puede definir como:
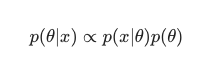
En este escenario, dejamos fuera el denominador como una simple medida anti-redundancia. Cualquier cosa que no cause dependencia del modelo puede ignorarse en el procedimiento de maximización. Esta pieza clave del rompecabezas, la distribución previa, es lo que permite que los modelos bayesianos se destaquen en contraste con sus contrapartes clásicas entrenadas en MLE.
Los analistas a menudo pueden hacer suposiciones razonables sobre qué tan adecuada es una configuración de parámetro específica, y esto contribuye en gran medida a codificar sus creencias sobre estos parámetros incluso antes de que los hayan visto en tiempo real. Es relativamente común, por ejemplo, utilizar una priorización gaussiana sobre los parámetros del modelo.
El analista aquí supone que estos parámetros se han extraído de una distribución normal, con cierta visualización tanto de la media como de la varianza. Este tipo de distribución presenta una forma clásica de curva de campana, consolidando una porción significativa de su masa, impresionantemente cerca de la media.
Por otro lado, las ocurrencias de valores hacia el final de la cola son bastante raras. El uso de tal anterior establece efectivamente la creencia de que la mayoría de los pesos del modelo deben encajar dentro de un rango estrecho definido , muy cerca del valor medio con solo unos pocos valores atípicos excepcionales. Esta es una creencia razonable a seguir, teniendo en cuenta los fenómenos del mundo real y las circunstancias no ideales.
Los efectos de un modelo bayesiano, sin embargo, son aún más interesantes cuando observa que el uso de estas distribuciones previas (y el proceso MAP ) genera resultados que son asombrosamente similares, si no iguales, a los que se resuelven realizando MLE en el sentido clásico. ayudado con alguna regularización adicional.
Es muy divertido notar que simplemente limitando los pesos del modelo "aceptado" con el anterior, terminamos creando un regularizador.
En general, el aprendizaje automático bayesiano está evolucionando rápidamente como un subcampo del aprendizaje automático, y un mayor desarrollo e incursión en el canon establecido parece ser un resultado bastante natural y probable del ritmo actual de avances en hardware computacional y estadístico.
Leer: Redes bayesianas
Los diferentes métodos de aprendizaje automático bayesiano
Hay tres enfoques ampliamente aceptados para el aprendizaje automático bayesiano, a saber, MAP , MCMC y el proceso "Gaussiano".
Aprendizaje automático bayesiano con MAP: máximo a posteriori
MAP disfruta de la distinción de ser el primer paso hacia el verdadero aprendizaje automático bayesiano. Sin embargo, tiene una capacidad limitada para calcular algo tan rudimentario como una estimación puntual, como comúnmente lo llaman los estadísticos experimentados.
El problema con las estimaciones puntuales es que no revelan mucho sobre un parámetro que no sea su configuración óptima. Los analistas y estadísticos a menudo buscan información valiosa central adicional, por ejemplo, la probabilidad de que el valor de un determinado parámetro se encuentre dentro de este rango predefinido. Después de todo, ahí es donde reside el verdadero poder predictivo del aprendizaje automático bayesiano.
Aprendizaje automático bayesiano con MCMC: Markov Chain Monte Carlo
Markov Chain Monte Carlo, también conocido comúnmente como MCMC, es un algoritmo "paraguas" popular y célebre, que se aplica a través de un conjunto de métodos subsidiarios famosos como Gibbs y Slice Sampling.
Y aunque las matemáticas de MCMC generalmente se consideran difíciles, siguen siendo igualmente intrigantes e impresionantes. La culminación de estos métodos subsidiarios es la construcción de una cadena de Markov conocida, asentándose además en una distribución que es equivalente a la posterior.
Muchos algoritmos sucesivos han optado por mejorar el método MCMC al incluir información de gradiente en un intento de permitir que los analistas naveguen por el espacio de parámetros con mayor eficiencia.
Sin embargo, hay formas más sencillas de lograr esta precisión. Por ejemplo, existen equivalentes de regresión logística y lineal bayesiana, en los que los analistas utilizan la aproximación de Laplace . Una aproximación analítica (que se puede explicar en papel) a la distribución posterior es lo que diferencia a este proceso.
Debe leer: Explicación de Naive Bayes
Aprendizaje automático bayesiano con el proceso gaussiano
El proceso gaussiano es un proceso estocástico, en el que se imponen condiciones gaussianas estrictas a todas las variables aleatorias constituyentes. Funcionan determinando una distribución de probabilidad sobre el espacio de todas las líneas posibles y luego seleccionando la línea que es más probable que sea el predictor real, teniendo en cuenta los datos.
Estos procesos terminan permitiendo a los analistas realizar una regresión en el espacio de funciones. Dado que toda la distribución posterior se calcula analíticamente con este método, esta es sin duda la estimación bayesiana en su forma más verdadera y, por lo tanto, tanto estadística como lógicamente, la más admirable.
Si desea obtener más información sobre carreras en aprendizaje automático e inteligencia artificial, consulte IIT Madras y la certificación avanzada en aprendizaje automático y nube de upGrad.