Pembelajaran Mesin Bayesian – Menjelajahi Pergeseran Paradigma Dalam Pemodelan Data Statistik
Diterbitkan: 2020-11-24Daftar isi
Apa itu Pembelajaran Mesin Bayesian?
Pembelajaran Mesin Bayesian (juga dikenal sebagai Bayesian ML) adalah pendekatan sistematis untuk membangun model statistik, berdasarkan Teorema Bayes.
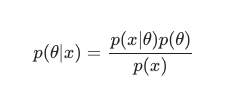Masalah pembelajaran mesin standar apa pun mencakup dua set data utama yang memerlukan analisis:
- Satu set lengkap data pelatihan
- Kumpulan dari semua input yang tersedia dan semua output yang direkam
Pendekatan tradisional untuk menganalisis data ini untuk pemodelan adalah menentukan beberapa pola yang dapat dipetakan di antara kumpulan data ini. Seorang analis biasanya akan menyatukan model untuk menentukan pemetaan antara ini, dan pendekatan yang dihasilkan adalah metode yang sangat deterministik untuk menghasilkan prediksi untuk variabel target.
Satu-satunya masalah adalah bahwa sama sekali tidak ada cara untuk menjelaskan apa yang terjadi di dalam model ini dengan serangkaian definisi yang jelas. Semua yang dicapai, pada dasarnya, adalah meminimalkan beberapa fungsi kerugian pada kumpulan data pelatihan – tetapi itu hampir tidak memenuhi syarat sebagai pemodelan yang sebenarnya .
Model yang ideal (dan lebih disukai, tanpa kerugian) memerlukan ringkasan objektif dari parameter bawaan model, dilengkapi dengan telur paskah statistik (seperti interval kepercayaan) yang dapat didefinisikan dan dipertahankan dalam bahasa probabilitas matematis. Skenario “ideal” inilah yang ingin dicapai oleh Pembelajaran Mesin Bayesian.
Tujuan (Dan Keajaiban) Pembelajaran Mesin Bayesian
Tujuan utama dari Pembelajaran Mesin Bayesian adalah untuk memperkirakan distribusi posterior , mengingat kemungkinan (perkiraan turunan dari data pelatihan) dan distribusi sebelumnya .
Saat melatih model pembelajaran mesin biasa, inilah yang akhirnya kami lakukan dalam teori dan praktik. Analis diketahui melakukan iterasi berturut-turut dari Estimasi Kemungkinan Maksimum pada data pelatihan, sehingga memperbarui parameter model dengan cara yang memaksimalkan kemungkinan melihat Ini mengarah ke masalah ayam-dan-telur, yang ingin dipecahkan oleh Pembelajaran Mesin Bayesian dengan indah.
Hal-hal mengambil giliran yang sama sekali berbeda dalam contoh tertentu di mana seorang analis berusaha untuk memaksimalkan distribusi posterior , dengan asumsi data pelatihan diperbaiki, dan dengan demikian menentukan probabilitas pengaturan parameter apa pun yang menyertai data tersebut. Proses ini disebut Maximum A Posteriori , disingkat MAP . Cara yang lebih mudah untuk memahami konsep ini adalah dengan memikirkannya dalam kaitannya dengan fungsi kemungkinan .
Dengan memperhatikan Teorema Bayes , posterior dapat didefinisikan sebagai:
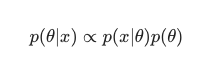
Dalam skenario ini, kami mengabaikan penyebut sebagai tindakan anti-redundansi sederhana. Segala sesuatu yang tidak menyebabkan ketergantungan pada model dapat diabaikan dalam prosedur maksimalisasi. Bagian kunci dari teka-teki ini, distribusi sebelumnya, adalah yang memungkinkan model Bayesian menonjol dibandingkan dengan model klasik yang dilatih MLE.
Analis sering dapat membuat asumsi yang masuk akal tentang seberapa cocok konfigurasi parameter tertentu, dan ini sangat membantu dalam mengkodekan keyakinan mereka tentang parameter ini bahkan sebelum mereka melihatnya secara real-time. Ini relatif biasa, misalnya, untuk menggunakan Gaussian sebelum parameter model.
Analis di sini mengasumsikan bahwa parameter ini telah diambil dari distribusi normal, dengan beberapa tampilan rata-rata dan varians. Distribusi semacam ini memiliki bentuk kurva lonceng klasik, mengkonsolidasikan sebagian besar massanya, sangat dekat dengan rata-rata.
Di sisi lain, kemunculan nilai di ujung ekor cukup jarang terjadi. Penggunaan prior seperti itu, secara efektif menyatakan keyakinan bahwa mayoritas bobot model harus sesuai dalam rentang sempit yang ditentukan , sangat dekat dengan nilai rata-rata dengan hanya beberapa outlier yang luar biasa. Ini adalah keyakinan yang masuk akal untuk dikejar, dengan mempertimbangkan fenomena dunia nyata dan keadaan yang tidak ideal.
Efek dari model Bayesian, bagaimanapun, bahkan lebih menarik ketika Anda mengamati bahwa penggunaan distribusi sebelumnya (dan proses MAP ) menghasilkan hasil yang sangat mirip, jika tidak sama dengan yang diselesaikan dengan melakukan MLE dalam pengertian klasik, dibantu dengan beberapa regularisasi tambahan.
Sangat lucu untuk dicatat bahwa hanya dengan membatasi bobot model "diterima" dengan prior, kami akhirnya membuat regulariser.
Secara keseluruhan, Pembelajaran Mesin Bayesian berkembang pesat sebagai subbidang pembelajaran mesin, dan pengembangan lebih lanjut dan terobosan ke dalam kanon yang mapan tampaknya merupakan hasil yang agak alami dan mungkin dari laju kemajuan perangkat keras komputasi dan statistik saat ini.
Baca: Bayesian Networks
Berbagai Metode Pembelajaran Mesin Bayesian
Ada tiga pendekatan yang diterima secara luas untuk Pembelajaran Mesin Bayesian, yaitu MAP , MCMC, dan proses “Gaussian”.
Pembelajaran Mesin Bayesian dengan MAP: Maksimum A Posteriori
MAP menikmati perbedaan sebagai langkah pertama menuju Pembelajaran Mesin Bayesian sejati. Namun, kemampuannya terbatas untuk menghitung sesuatu yang belum sempurna seperti perkiraan titik, seperti yang biasa disebut oleh ahli statistik berpengalaman.
Masalah dengan perkiraan titik adalah bahwa mereka tidak mengungkapkan banyak tentang parameter selain pengaturan optimalnya. Analis dan ahli statistik sering kali mencari informasi tambahan yang berharga, misalnya, kemungkinan nilai parameter tertentu berada dalam kisaran yang telah ditentukan ini. Lagi pula, di situlah kekuatan prediksi nyata dari Pembelajaran Mesin Bayesian berada.
Pembelajaran Mesin Bayesian dengan MCMC: Markov Chain Monte Carlo
Markov Chain Monte Carlo, juga dikenal secara umum sebagai MCMC, adalah algoritma "payung" yang populer dan terkenal, diterapkan melalui serangkaian metode anak perusahaan yang terkenal seperti Gibbs dan Slice Sampling.
Dan sementara matematika MCMC umumnya dianggap sulit, itu tetap sama menarik dan mengesankan. Puncak dari metode anak perusahaan ini, adalah pembangunan rantai Markov yang dikenal, selanjutnya menetap menjadi distribusi yang setara dengan posterior.
Banyak algoritma berturut-turut telah memilih untuk memperbaiki metode MCMC dengan memasukkan informasi gradien dalam upaya untuk membiarkan analis menavigasi ruang parameter dengan peningkatan efisiensi.
Namun, ada cara yang lebih sederhana untuk mencapai akurasi ini. Misalnya, ada persamaan regresi linier dan logistik Bayesian, di mana analis menggunakan Pendekatan Laplace . Pendekatan analitis (yang dapat dijelaskan di atas kertas) ke distribusi posterior adalah yang membedakan proses ini.
Harus Dibaca: Penjelasan Naive Bayes
Pembelajaran Mesin Bayesian dengan proses Gaussian
Proses Gaussian adalah proses stokastik, dengan kondisi Gaussian yang ketat diterapkan pada semua konstituen, variabel acak. Mereka bekerja dengan menentukan distribusi probabilitas di atas ruang semua garis yang mungkin dan kemudian memilih garis yang paling mungkin menjadi prediktor sebenarnya, dengan mempertimbangkan data.
Proses ini akhirnya memungkinkan analis untuk melakukan regresi di ruang fungsi. Mengingat bahwa seluruh distribusi posterior sedang dihitung secara analitik dalam metode ini, ini tidak diragukan lagi merupakan estimasi Bayesian yang paling benar, dan karena itu baik secara statistik maupun logis, yang paling mengagumkan.
Jika Anda ingin tahu lebih banyak tentang karier di Pembelajaran Mesin dan Kecerdasan Buatan, lihat IIT Madras dan Sertifikasi Lanjutan upGrad dalam Pembelajaran Mesin dan Cloud.