Redes convolucionales gráficas: Lista de aplicaciones que necesita saber

La red convolucional es un tipo de red neuronal. Las redes neuronales son un tipo especial de modelo de aprendizaje profundo. Por lo general, el aprendizaje automático o el aprendizaje profundo comprende algoritmos rigurosos y costosos debido a su tarea complicada. Del mismo modo, los modelos de aprendizaje profundo en gráficos son aún más complicados. Las redes convolucionales gráficas se utilizan principalmente con el propósito de clasificar imágenes. Obtenga más información sobre la red neuronal convolucional.

Durante la última década, la aplicación de la ciencia de datos ha aumentado enormemente. En este mundo rico en datos, el enfoque del modelo de aprendizaje trajo excelentes resultados y predicciones precisas. Los gráficos son útiles para muchos sistemas de información.

Desde interacciones de proteínas biológicas hasta conectividad a Internet y WorldWideWeb, los gráficos representan todos estos sistemas. Además, la implementación de redes neuronales a través de una estructura gráfica le permite a la computadora comprender las propiedades de una imagen. Este modelo es una de las aplicaciones más avanzadas del gráfico en el mundo real. Analicemos estos algoritmos en detalle:

Cómo se construyen las redes neuronales

Las redes neuronales son una de las técnicas más avanzadas de ciencia de datos y aprendizaje profundo. Las redes neuronales son útiles en muchas aplicaciones, desde la predicción del mercado de valores hasta la clasificación de imágenes, el reconocimiento de voz o caracteres e incluso en el análisis de secuencias.

El primer concepto de Red Neuronal provino de perspectivas biológicas. Los científicos realizaron experimentos en los que los nervios para la visión están conectados con los centros auditivos del cerebro. Eventualmente, el organismo también aprendió a ver a través del centro auditivo del cerebro. Incluso experimentos posteriores demostraron que todos los centros del cerebro podían realizar todas las acciones.

Los enfoques comenzaron a comenzar a imitar el cerebro humano informando algoritmos informáticos. Entonces, de manera similar, los científicos informáticos también pensaron que debería haber un algoritmo único que sea capaz de resolver todos los problemas de aprendizaje del cerebro de la computadora. Así nació la red neuronal.

Una red neuronal consta de varias capas de neuronas. Cada neurona es típicamente un nodo gráfico. Cada neurona de cada capa está conectada con todas las neuronas de la siguiente capa a través de un borde ponderado: los pesos del borde actúan como un coeficiente del cálculo del valor de la capa.

A través de la retropropagación, los coeficientes cambian para ajustarse al modelo con ejemplos de entrenamiento de muestra. En última instancia, una sola neurona de la última capa da la salida. En la siguiente imagen se explica la estructura de una red neuronal.

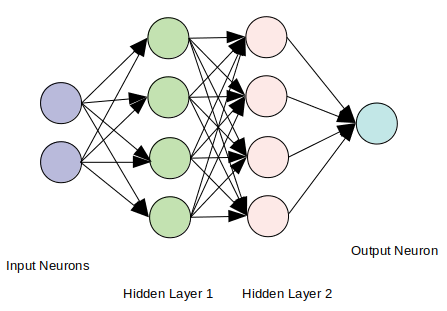
Fuente de imagen

Leer: Uso de la red neuronal convolucional para la clasificación de imágenes

Graficar redes convolucionales

Las redes convolucionales son redes neuronales tridimensionales. La mayoría de los usos prácticos de las redes neuronales convolucionales incluyen la clasificación y el reconocimiento de imágenes, el procesamiento del lenguaje natural y el reconocimiento del habla. Estos modelos suelen ser más complejos que los modelos de redes neuronales bidimensionales habituales.

En esta arquitectura se ensamblan capas de diferentes neuronas. El parámetro de dimensiones es variable en diferentes capas para que el modelo reconozca los parámetros. Por ejemplo, las imágenes son bidimensionales y, mientras tanto, el color de cada punto también juega un papel crucial. Por lo tanto, surgen tres parámetros diferentes. Para lidiar con tales complejidades, Conv Nets juega un papel importante.

Estas muchas matrices 3D de diferentes dimensiones funcionan en múltiples niveles de la red neuronal. Eventualmente, la dimensión 'z' se ajusta al parámetro de salida de la red. El transporte de información de un nivel a otro puede tener lugar a través de una variedad de algoritmos diferentes.

Por ejemplo, FC (Fully Connected), Pooling y ReLU son algunos algoritmos cruciales con respecto a esto.

En general, los valores de nodo de la red neuronal se indican con, donde 'l' significa el número de capa. Entonces, un 0 es la matriz de entrada.

un 0 =X

Por otro lado, el último nodo de capa define la salida. Digamos, hay capas 'L'. Por lo tanto , una L denota la salida de la red neuronal.

una L = Y

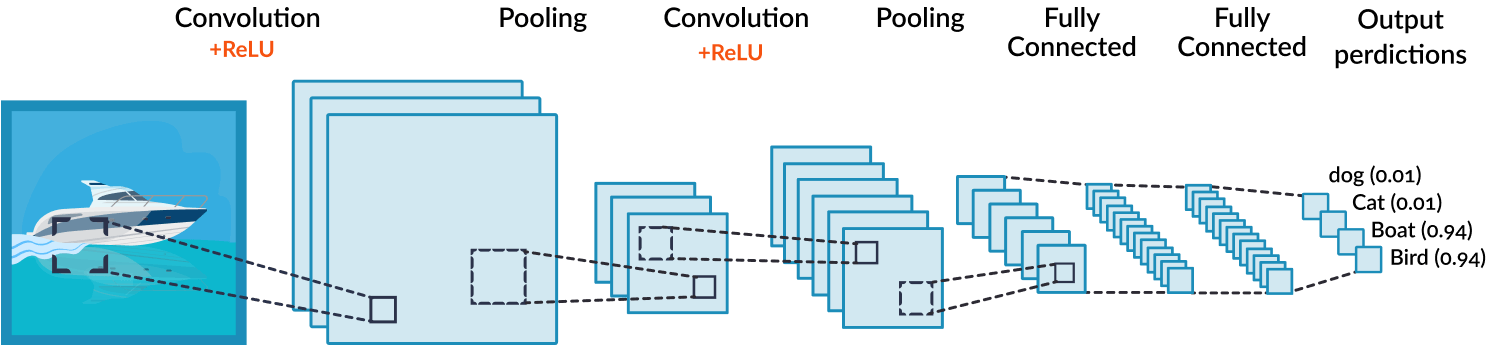
Fuente de imagen

La imagen de arriba muestra una red neuronal convolucional en la implementación de la clasificación de imágenes. Los parámetros se establecen para un perro, un gato, un murciélago y un pájaro.

El valor de nodo de una capa interna particular se calcula a través de valores de capas anteriores.

un l+1 =f( un l ,θ)

Aquí, es la matriz de adyacencia y f es la función definitoria. Cada capa de red convolucional gráfica se puede escribir usando esta expresión. De esta manera, una red neuronal convolucional de gráficos suele funcionar.

Aplicaciones de Redes Convolucionales de Grafos

• Las redes convolucionales gráficas generan predicciones sobre sistemas físicos, como gráficos, su enfoque interactivo y aplicaciones. GCN también proporciona información precisa sobre las propiedades de las entidades del mundo real y los sistemas físicos (dinámica de la colisión, trayectorias de objetos).
• Los GCN se utilizan para realizar problemas de diferenciación de imágenes. El modelo que sigue se conoce como 'Zero-Shot Learning'. El motivo principal de este modelo es identificar una imagen etiquetada desconocida y agruparla en las conocidas. También recopilan información semántica de estas etiquetas y las categorizan.
• Los GCN pueden tomar una cierta longitud de huellas dactilares moleculares como entrada y generar estructuras moleculares predichas. MolGAN es un tipo de red Graph Convolucional que ayuda a crear nuevas estructuras moleculares con varias características. De esta forma, permite a los científicos inventar estructuras moleculares modernas día a día.
• GCN es aplicable para resolver varios problemas relacionados con operaciones de investigación y aplicaciones de optimización combinatoria. Las redes convolucionales gráficas desempeñan un papel fundamental en la resolución de problemas de vendedores, problemas de asignación cuadrática y muchos más. Con la ayuda del gráfico de entrada, puede superar a los algoritmos complejos tradicionales.

Club de Karate de Zachary

Otra aplicación importante de Graph Convolutional Networks es resolver problemas de predicción de la comunidad, como Karate Club of Zachary. Este problema se basa en la disputa entre el administrador y el instructor del club.

Tenemos que averiguar qué lado elegiría cada miembro del club de karate. Este problema se resuelve utilizando técnicas de aprendizaje semisupervisado. Al usar solo dos nodos etiquetados, Tobias Jepsen pudo solucionar el problema y alcanzar una precisión casi perfecta en términos de predicción de esas dos comunidades.

Ahora echemos un vistazo a las siguientes imágenes y podrá obtener algunas ideas sobre el problema del club de Karate y sus cálculos adecuados utilizando Graph Convolutional Networks.

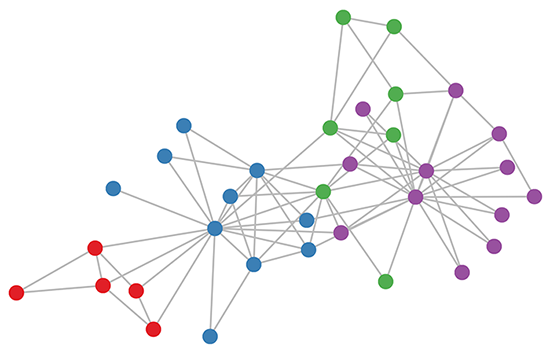
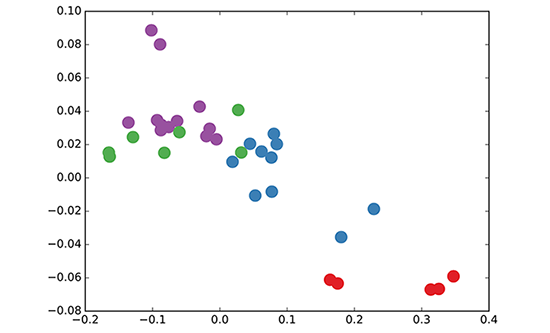
Fuente de imagen

Lea también: Ideas de proyectos de redes neuronales

Terminando

Al leer este artículo, podrá comprender qué son las redes convolucionales gráficas, cómo se construyen las redes neuronales, una breve idea de GCN y cómo funciona, y varios aspectos y aplicaciones cruciales de GCN, incluido el problema de Zachary Karate Club.

Si desea obtener más información sobre GCN y sus características y beneficios, regístrese en upGrad Education Pvt. Ltd. Y el curso de posgrado y diplomado de IIITB en Machine Learning e Inteligencia Artificial . Este curso sobre Machine Learning e IA está diseñado para estudiantes y profesionales que trabajan.

El curso proporciona una colección de estudios de casos y asignaciones, sesiones de tutoría de la industria, estado de ex alumnos de IIIT Bangalore, asistencia para la colocación laboral en las mejores empresas y, lo que es más importante, una rica experiencia de aprendizaje.