ベイジアン機械学習–統計データモデリングのパラダイムシフトを探る
公開: 2020-11-24目次
ベイジアン機械学習とは何ですか?
ベイジアン機械学習(ベイジアンMLとも呼ばれます)は、ベイズの定理に基づいて統計モデルを構築するための体系的なアプローチです。
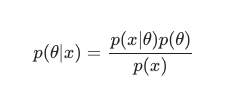 標準的な機械学習の問題には、分析が必要な2つの主要なデータセットが含まれます。
標準的な機械学習の問題には、分析が必要な2つの主要なデータセットが含まれます。
- トレーニングデータの包括的なセット
- 利用可能なすべての入力と記録されたすべての出力のコレクション
モデリングのためにこのデータを分析する従来のアプローチは、これらのデータセット間でマッピングできるいくつかのパターンを決定することです。 アナリストは通常、モデルをつなぎ合わせてこれらの間のマッピングを決定します。結果として得られるアプローチは、ターゲット変数の予測を生成するための非常に決定論的な方法です。
唯一の問題は、このモデル内で何が起こっているのかを明確な定義で説明する方法がまったくないということです。 基本的に、達成されるのはトレーニングデータセットの一部の損失関数を最小化することだけですが、それは真のモデリングとは言えません。
理想的な(そしてできれば無損失の)モデルは、数学的確率の言語で定義および防御できる統計的イースターエッグ(信頼区間など)で補足された、モデルの固有のパラメーターの客観的な要約を伴います。 この「理想的な」シナリオは、ベイジアン機械学習が達成しようとしていることです。
ベイジアン機械学習の目標(および魔法)
ベイジアン機械学習の主な目的は、尤度(トレーニングデータの微分推定値)と事前分布を前提として、事後分布を推定することです。

通常の機械学習モデルをトレーニングする場合、これはまさに私たちが理論と実践で行うことになることです。 アナリストは、トレーニングデータに対して最尤推定を連続して繰り返し実行することが知られています。これにより、モデルには既にパラメーターの一応の可視性があるため、それは鶏が先か卵が先かという問題につながり、ベイジアン機械学習はそれを美しく解決することを目指しています。
トレーニングデータが固定されていると仮定して、アナリストが事後分布をこのプロセスは最大事後確率と呼ばれ、 MAPと短縮されます。 この概念を理解するためのより簡単な方法は、尤度関数の観点からそれを考えることです。
ベイズの定理を考慮に入れると、後部は次のように定義できます。
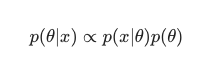
このシナリオでは、単純な冗長性対策として分母を省略します。 モデルへの依存を引き起こさないものはすべて、最大化手順では無視できます。 パズルのこの重要な部分である事前分布は、ベイジアンモデルを従来のMLEトレーニング済みのモデルとは対照的に際立たせるものです。
アナリストは、特定のパラメーター構成がどの程度適しているかについて合理的な仮定を立てることができます。これは、リアルタイムでパラメーターを確認する前であっても、これらのパラメーターに関する信念をエンコードするのに大いに役立ちます。 たとえば、モデルのパラメータよりも前にガウス分布を使用することは比較的一般的です。

ここでのアナリストは、これらのパラメーターが正規分布から抽出され、平均と分散の両方が表示されていると想定しています。 この種の分布は、古典的なベルカーブの形状を特徴としており、その質量のかなりの部分を平均に非常に近い形で統合しています。
一方、テールエンドに向かって値が発生することは非常にまれです。 このような事前分布の使用は、モデルの重みの大部分が定義された狭い範囲内に収まらなければならないという信念を効果的に示しています。 これは、現実世界の現象と非理想的な状況を考慮に入れて、追求する合理的な信念です。
ただし、ベイジアンモデルの効果は、これらの事前分布(およびMAPプロセス)を使用すると、古典的な意味でMLEを実行して解決された結果と等しくない場合でも、驚くほど類似した結果が生成されることを確認すると、さらに興味深いものになります。いくつかの追加の正則化を支援しました。
「受け入れられた」モデルの重みを以前のモデルの重みで制約するだけで、最終的にレギュラライザーが作成されることに注意するのは非常に面白いです。
全体として、ベイジアン機械学習は機械学習のサブフィールドとして急速に進化しており、確立された標準へのさらなる開発と侵入は、計算および統計ハードウェアの現在の進歩のペースのかなり自然でありそうな結果であるように見えます。
読む:ベイジアンネットワーク
ベイジアン機械学習のさまざまな方法
ベイジアン機械学習には、 MAP 、MCMC、および「ガウス」プロセスの3つの広く受け入れられているアプローチがあります。
MAPを使用したベイジアン機械学習:最大事後確率
MAPは、真のベイジアン機械学習への第一歩であるという特徴を享受しています。 ただし、経験豊富な統計家が一般的に言及しているように、点推定と同じくらい基本的なものを計算する能力には限界があります。
点推定の問題は、最適な設定以外のパラメーターについてはあまり明らかにされないことです。 アナリストや統計家は、多くの場合、追加のコアとなる貴重な情報を追求しています。たとえば、特定のパラメーターの値がこの事前定義された範囲内に収まる確率などです。 結局のところ、そこにベイジアン機械学習の真の予測力があります。
MCMCを使用したベイジアン機械学習:マルコフ連鎖モンテカルロ
一般にMCMCとしても知られているマルコフ連鎖モンテカルロ法は、人気があり有名な「傘」アルゴリズムであり、ギブスやスライスサンプリングなどの有名な補助的な方法のセットを介して適用されます。
そして、MCMCの数学は一般的に難しいと考えられていますが、同様に興味深く印象的なままです。 これらの補助的な方法の集大成は、既知のマルコフ連鎖の構築であり、後部と同等の分布にさらに落ち着きます。
多くの連続したアルゴリズムは、アナリストが効率を高めてパラメータ空間をナビゲートできるようにするために、勾配情報を含めることによってMCMC法を改善することを選択しました。

ただし、この精度を達成するためのより簡単な方法があります。 たとえば、ベイズ線形回帰とロジスティック回帰に相当するものがあり、アナリストはラプラス近似を使用します。 事後分布の分析的近似(紙で説明できます)が、このプロセスを際立たせています。
必読:ナイーブベイズの説明
ガウス過程によるベイジアン機械学習
ガウス過程は確率過程であり、すべての構成要素である確率変数に厳密なガウス条件が課されます。 それらは、すべての可能な線の空間にわたる確率分布を決定し、データを考慮に入れて、実際の予測子である可能性が最も高い線を選択することによって機能します。
これらのプロセスにより、アナリストは関数空間で回帰を実行できるようになります。 事後分布全体がこの方法で分析的に計算されていることを考えると、これは間違いなくベイズ推定であり、したがって統計的にも論理的にも最も称賛に値します。
機械学習と人工知能のキャリアについて詳しく知りたい場合は、IITマドラスとupGradの機械学習とクラウドの高度な認定を確認してください。
