Aprendizado de máquina bayesiano – explorando uma mudança de paradigma na modelagem de dados estatísticos
Publicados: 2020-11-24Índice
O que é Aprendizado de Máquina Bayesiano?
Bayesian Machine Learning (também conhecido como Bayesian ML) é uma abordagem sistemática para construir modelos estatísticos, com base no Teorema de Bayes.
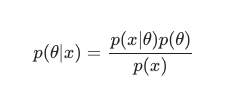Qualquer problema de aprendizado de máquina padrão inclui dois conjuntos de dados primários que precisam de análise:
- Um conjunto abrangente de dados de treinamento
- Uma coleção de todas as entradas disponíveis e todas as saídas gravadas
A abordagem tradicional para analisar esses dados para modelagem é determinar alguns padrões que podem ser mapeados entre esses conjuntos de dados. Um analista geralmente unirá um modelo para determinar o mapeamento entre eles, e a abordagem resultante é um método muito determinístico para gerar previsões para uma variável de destino.
O único problema é que não há absolutamente nenhuma maneira de explicar o que está acontecendo dentro desse modelo com um conjunto claro de definições. Tudo o que é realizado, essencialmente, é a minimização de algumas funções de perda no conjunto de dados de treinamento – mas isso dificilmente se qualifica como modelagem verdadeira .
Um modelo ideal (e preferencialmente sem perdas) envolve um resumo objetivo dos parâmetros inerentes ao modelo, complementado com easter eggs estatísticos (como intervalos de confiança) que podem ser definidos e defendidos na linguagem da probabilidade matemática. Esse cenário “ideal” é o que o Bayesian Machine Learning se propõe a realizar.
Os objetivos (e magia) do aprendizado de máquina bayesiano
O objetivo principal do Aprendizado de Máquina Bayesiano é estimar a distribuição a posteriori , dada a probabilidade (uma estimativa derivada dos dados de treinamento) e a distribuição a priori .
Ao treinar um modelo regular de aprendizado de máquina, é exatamente isso que acabamos fazendo na teoria e na prática. Os analistas são conhecidos por realizar sucessivas iterações de Estimativa de Máxima Verossimilhança nos dados de treinamento, atualizando assim os parâmetros do modelo de forma a maximizar a probabilidade de ver os Isso leva a um problema do ovo e da galinha, que o Aprendizado de Máquina Bayesiano visa resolver lindamente.
As coisas tomam um rumo totalmente diferente em uma determinada instância em que um analista procura maximizar a distribuição posterior , assumindo que os dados de treinamento sejam fixos e, assim, determinando a probabilidade de qualquer configuração de parâmetro que acompanhe esses dados. Este processo é chamado de Maximum A Posteriori , abreviado como MAP . Uma maneira mais fácil de entender esse conceito é pensar sobre ele em termos da função de verossimilhança .
Levando em conta o Teorema de Bayes , a posterior pode ser definida como:
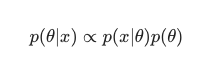
Nesse cenário, deixamos de fora o denominador como uma simples medida anti-redundância. Qualquer coisa que não cause dependência do modelo pode ser ignorada no procedimento de maximização. Essa peça-chave do quebra-cabeça, a distribuição prévia, é o que permite que os modelos Bayesianos se destaquem em contraste com suas contrapartes clássicas treinadas em MLE.
Os analistas geralmente podem fazer suposições razoáveis sobre a adequação de uma configuração de parâmetro específica, e isso ajuda bastante na codificação de suas crenças sobre esses parâmetros antes mesmo de vê-los em tempo real. É relativamente comum, por exemplo, usar uma anterior gaussiana sobre os parâmetros do modelo.
O analista aqui está assumindo que esses parâmetros foram extraídos de uma distribuição normal, com alguma exibição de média e variância. Esse tipo de distribuição apresenta uma forma clássica de sino-curva, consolidando uma parcela significativa de sua massa, impressionantemente próxima à média.
Por outro lado, ocorrências de valores no final da cauda são bastante raras. O uso de tal prior, efetivamente, afirma a crença de que a maioria dos pesos do modelo deve caber dentro de uma faixa estreita definida , muito próxima do valor médio com apenas alguns outliers excepcionais. Esta é uma crença razoável a ser perseguida, levando em consideração fenômenos do mundo real e circunstâncias não ideais.
Os efeitos de um modelo Bayesiano, no entanto, são ainda mais interessantes quando você observa que o uso dessas distribuições anteriores (e do processo MAP ) gera resultados surpreendentemente semelhantes, se não iguais aos resolvidos pela execução de MLE no sentido clássico, auxiliou com alguma regularização adicional.
É muito divertido notar que apenas restringindo os pesos do modelo “aceitos” com o anterior, acabamos criando um regularizador.
No geral, o aprendizado de máquina bayesiano está evoluindo rapidamente como um subcampo do aprendizado de máquina, e o desenvolvimento e as incursões no cânone estabelecido parecem ser um resultado bastante natural e provável do ritmo atual de avanços em hardware computacional e estatístico.
Leia: Redes Bayesianas
Os diferentes métodos de aprendizado de máquina bayesiano
Existem três abordagens amplamente aceitas para o Aprendizado de Máquina Bayesiano, a saber, MAP , MCMC e o processo “Gaussiano”.
Aprendizado de Máquina Bayesiano com MAP: Máximo A Posteriori
O MAP tem a distinção de ser o primeiro passo para o verdadeiro aprendizado de máquina bayesiano. No entanto, é limitado em sua capacidade de calcular algo tão rudimentar quanto uma estimativa pontual, como comumente referido por estatísticos experientes.
O problema com as estimativas pontuais é que elas não revelam muito sobre um parâmetro além de sua configuração ideal. Analistas e estatísticos muitas vezes estão em busca de informações valiosas adicionais, por exemplo, a probabilidade de o valor de um determinado parâmetro cair dentro dessa faixa predefinida. Afinal, é aí que reside o verdadeiro poder preditivo do Aprendizado de Máquina Bayesiano.
Aprendizado de máquina bayesiano com MCMC: Markov Chain Monte Carlo
Markov Chain Monte Carlo, também conhecido comumente como MCMC, é um algoritmo “guarda-chuva” popular e celebrado, aplicado através de um conjunto de métodos subsidiários famosos, como Gibbs e Slice Sampling.
E embora a matemática do MCMC seja geralmente considerada difícil, continua sendo igualmente intrigante e impressionante. A culminação desses métodos subsidiários é a construção de uma cadeia de Markov conhecida, estabelecendo-se ainda uma distribuição equivalente à posterior.
Muitos algoritmos sucessivos optaram por melhorar o método MCMC, incluindo informações de gradiente na tentativa de permitir que os analistas naveguem no espaço de parâmetros com maior eficiência.
No entanto, existem maneiras mais simples de obter essa precisão. Por exemplo, existem equivalentes de regressão linear e logística Bayesiana, nos quais os analistas usam a Aproximação de Laplace . Uma aproximação analítica (que pode ser explicada no papel) para a distribuição a posteriori é o que diferencia esse processo.
Deve ler: Naive Bayes explicado
Aprendizado de máquina bayesiano com o processo gaussiano
O processo gaussiano é um processo estocástico, com condições gaussianas estritas sendo impostas a todas as variáveis aleatórias constituintes. Eles funcionam determinando uma distribuição de probabilidade no espaço de todas as linhas possíveis e, em seguida, selecionando a linha que mais provavelmente será o preditor real, levando os dados em consideração.
Esses processos acabam permitindo que os analistas realizem a regressão no espaço funcional. Dado que toda a distribuição posterior está sendo computada analiticamente neste método, esta é, sem dúvida, a estimativa Bayesiana em sua forma mais verdadeira e, portanto, estatística e logicamente, a mais admirável.
Se você quiser saber mais sobre carreiras em Machine Learning e Inteligência Artificial, confira IIT Madras e a Certificação Avançada do upGrad em Machine Learning e Cloud.