Machine learning bayesiano: esplorare un cambiamento di paradigma nella modellazione dei dati statistici
Pubblicato: 2020-11-24Sommario
Che cos'è l'apprendimento automatico bayesiano?
Bayesian Machine Learning (noto anche come Bayesian ML) è un approccio sistematico per costruire modelli statistici, basato sul teorema di Bayes.
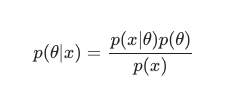Qualsiasi problema di machine learning standard include due set di dati primari che necessitano di analisi:
- Un set completo di dati di allenamento
- Una raccolta di tutti gli input disponibili e di tutti gli output registrati
L'approccio tradizionale all'analisi di questi dati per la modellazione consiste nel determinare alcuni modelli che possono essere mappati tra questi set di dati. Un analista di solito unisce un modello per determinare la mappatura tra questi e l'approccio risultante è un metodo molto deterministico per generare previsioni per una variabile target.
L'unico problema è che non c'è assolutamente modo di spiegare cosa sta succedendo all'interno di questo modello con una chiara serie di definizioni. Tutto ciò che si ottiene, in sostanza, è la minimizzazione di alcune funzioni di perdita sul set di dati di addestramento, ma ciò difficilmente si qualifica come una vera modellazione.
Un modello ideale (e preferibilmente senza perdite) comporta un riassunto oggettivo dei parametri intrinseci del modello, integrato con easter egg statistici (come gli intervalli di confidenza) che possono essere definiti e difesi nel linguaggio della probabilità matematica. Questo scenario "ideale" è ciò che il Machine Learning bayesiano si propone di realizzare.
Gli obiettivi (e la magia) dell'apprendimento automatico bayesiano
L'obiettivo principale dell'apprendimento automatico bayesiano è stimare la distribuzione a posteriori , data la probabilità (una stima derivata dei dati di addestramento) e la distribuzione a priori .
Quando si addestra un modello di apprendimento automatico regolare, questo è esattamente ciò che si finisce per fare in teoria e pratica. È noto che gli analisti eseguono iterazioni successive della stima della massima verosimiglianza sui dati di addestramento, aggiornando così i parametri del modello in modo da massimizzare la probabilità di vedere i Porta a un problema di gallina e uova, che l'apprendimento automatico bayesiano mira a risolvere magnificamente.
Le cose prendono una piega completamente diversa in un dato caso in cui un analista cerca di massimizzare la distribuzione a posteriori , supponendo che i dati di addestramento siano fissi e determinando così la probabilità di qualsiasi impostazione di parametro che accompagna detti dati. Questo processo è chiamato Massimo A Posteriori , abbreviato in MAP . Un modo più semplice per afferrare questo concetto è pensarlo in termini di funzione di verosimiglianza .
Tenendo conto del teorema di Bayes , il posteriore può essere definito come:
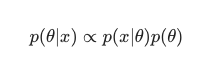
In questo scenario, tralasciamo il denominatore come semplice misura anti-ridondanza. Tutto ciò che non causa dipendenza dal modello può essere ignorato nella procedura di massimizzazione. Questo pezzo chiave del puzzle, la distribuzione preventiva, è ciò che consente ai modelli bayesiani di distinguersi in contrasto con le loro controparti classiche addestrate al MLE.
Gli analisti possono spesso fare ipotesi ragionevoli su quanto sia adatta una configurazione di parametro specifica, e questo aiuta molto a codificare le loro convinzioni su questi parametri anche prima di averli visti in tempo reale. È relativamente comune, ad esempio, utilizzare una priorità gaussiana sui parametri del modello.
L'analista qui presuppone che questi parametri siano stati tratti da una distribuzione normale, con qualche visualizzazione sia della media che della varianza. Questo tipo di distribuzione presenta una classica forma a campana, consolidando una porzione significativa della sua massa, impressionantemente vicino alla media.
D'altra parte, le occorrenze di valori verso la coda sono piuttosto rare. L'uso di tale prior, afferma effettivamente la convinzione che la maggior parte dei pesi del modello deve rientrare in un intervallo ristretto definito , molto vicino al valore medio con solo pochi valori anomali eccezionali. Questa è una convinzione ragionevole da perseguire, tenendo in considerazione i fenomeni del mondo reale e le circostanze non ideali.
Gli effetti di un modello bayesiano, tuttavia, sono ancora più interessanti se si osserva che l'uso di queste distribuzioni a priori (e il processo MAP ) genera risultati sorprendentemente simili, se non uguali a quelli risolti eseguendo MLE in senso classico, aiutato con qualche regolarizzazione aggiuntiva.
È molto divertente notare che semplicemente vincolando i pesi del modello "accettati" con il precedente, finiamo per creare un regolarizzatore.
Nel complesso, l'apprendimento automatico bayesiano si sta evolvendo rapidamente come sottocampo dell'apprendimento automatico e l'ulteriore sviluppo e le incursioni nel canone stabilito sembrano essere un risultato piuttosto naturale e probabile dell'attuale ritmo di progressi nell'hardware computazionale e statistico.
Leggi: Reti bayesiane
I diversi metodi di apprendimento automatico bayesiano
Esistono tre approcci ampiamente accettati per l'apprendimento automatico bayesiano, vale a dire MAP , MCMC e il processo "gaussiano".
Machine Learning bayesiano con MAP: Massimo A Posteriori
MAP gode della particolarità di essere il primo passo verso il vero Machine Learning bayesiano. Tuttavia, è limitato nella sua capacità di calcolare qualcosa di così rudimentale come una stima puntuale, come comunemente indicato da esperti di statistica.
Il problema con le stime puntuali è che non rivelano molto su un parametro diverso dalla sua impostazione ottimale. Gli analisti e gli statistici sono spesso alla ricerca di ulteriori informazioni di valore fondamentale, ad esempio la probabilità che il valore di un determinato parametro rientri in questo intervallo predefinito. Dopotutto, è qui che risiede il vero potere predittivo del Machine Learning bayesiano.
Machine Learning bayesiano con MCMC: Markov Chain Monte Carlo
Markov Chain Monte Carlo, noto anche comunemente come MCMC, è un popolare e celebre algoritmo "ombrello", applicato attraverso una serie di famosi metodi sussidiari come Gibbs e Slice Sampling.
E mentre la matematica di MCMC è generalmente considerata difficile, rimane ugualmente intrigante e impressionante. Il culmine di questi metodi sussidiari è la costruzione di una nota catena di Markov, che si stabilisce ulteriormente in una distribuzione equivalente a quella posteriore.
Molti algoritmi successivi hanno scelto di migliorare il metodo MCMC includendo informazioni sul gradiente nel tentativo di consentire agli analisti di navigare nello spazio dei parametri con maggiore efficienza.
Tuttavia, esistono modi più semplici per ottenere questa precisione. Ad esempio, esistono equivalenti di regressione lineare e logistica bayesiana, in cui gli analisti utilizzano l' approssimazione di Laplace . Un'approssimazione analitica (che può essere spiegata su carta) alla distribuzione a posteriori è ciò che distingue questo processo.
Da leggere: Spiegazione di Naive Bayes
Machine Learning bayesiano con il processo gaussiano
Il processo gaussiano è un processo stocastico, con condizioni gaussiane rigorose imposte a tutte le variabili casuali costituenti. Funzionano determinando una distribuzione di probabilità nello spazio di tutte le linee possibili e quindi selezionando la linea che è più probabile che sia il predittore effettivo, tenendo conto dei dati.
Questi processi finiscono per consentire agli analisti di eseguire la regressione nello spazio delle funzioni. Dato che l' intera distribuzione a posteriori viene calcolata analiticamente in questo metodo, questa è senza dubbio la stima bayesiana nella sua forma più vera, e quindi sia statisticamente che logicamente, la più ammirevole.
Se vuoi saperne di più sulle carriere in Machine Learning e Intelligenza Artificiale, dai un'occhiata a IIT Madras e alla certificazione avanzata di upGrad in Machine Learning e Cloud.