贝叶斯机器学习——探索统计数据建模的范式转变
已发表: 2020-11-24目录
什么是贝叶斯机器学习？
贝叶斯机器学习（也称为贝叶斯机器学习）是一种基于贝叶斯定理构建统计模型的系统方法。
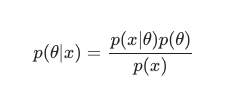任何标准的机器学习问题都包括两个需要分析的主要数据集：
- 一套全面的训练数据
- 所有可用输入和所有记录输出的集合
分析这些数据以进行建模的传统方法是确定可以在这些数据集之间映射的一些模式。 分析师通常会将模型拼接在一起以确定这些模型之间的映射，由此产生的方法是一种非常确定的方法来生成目标变量的预测。
唯一的问题是，绝对没有办法用一套清晰的定义来解释这个模型内部发生的事情。 本质上，所完成的只是最小化训练数据集上的一些损失函数——但这几乎不能算作真正的建模。
一个理想的（最好是无损的）模型需要对模型的固有参数进行客观总结，并辅以可以用数学概率语言定义和维护的统计彩蛋（例如置信区间）。 这种“理想”的场景是贝叶斯机器学习想要完成的。
贝叶斯机器学习的目标（和魔法）
贝叶斯机器学习的主要目标是估计后验分布，给定可能性（训练数据的导数估计）和先验分布。
在训练常规机器学习模型时，这正是我们最终在理论和实践中所做的事情。 众所周知，分析师会对训练数据执行最大似然估计的连续迭代，从而以最大化看到它导致了一个先有鸡还是先有蛋的问题，贝叶斯机器学习旨在完美地解决这个问题。
假设训练数据是固定的，从而确定伴随所述数据的任何参数设置的概率，分析师寻求这个过程称为Maximum A Postiori ，简称为MAP 。 掌握这个概念的一个更简单的方法是根据似然函数来考虑它。
考虑到贝叶斯定理，后验可以定义为：
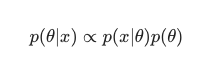
在这种情况下，我们将分母作为一种简单的反冗余措施排除在外。 在最大化过程中可以忽略任何不会导致对模型的依赖。 这个难题的关键部分，即先验分布，是让贝叶斯模型与经典的 MLE 训练模型相比脱颖而出的原因。
分析师通常可以对特定参数配置的适合程度做出合理的假设，这对编码他们对这些参数的看法大有帮助，甚至在他们实时看到这些参数之前。 例如，在模型参数上使用高斯先验是相对常见的。
这里的分析师假设这些参数是从正态分布中提取的，其中显示了均值和方差。 这种分布具有经典的钟形曲线形状，巩固了其质量的很大一部分，令人印象深刻地接近平均值。
另一方面，尾部值的出现非常罕见。 使用这样的先验，有效地表明了这样一种信念，即模型的大多数权重必须符合定义的狭窄范围，非常接近平均值，只有少数异常异常值。 考虑到现实世界的现象和非理想情况，这是一个合理的信念。
然而，当您观察到使用这些先验分布（和MAP过程）产生的结果惊人地相似时，贝叶斯模型的效果会更加有趣，如果不等于通过执行经典意义上的 MLE 解决的结果，辅助一些额外的正则化。
有趣的是，仅通过使用先验约束“接受的”模型权重，我们最终创建了一个正则化器。
总体而言，贝叶斯机器学习作为机器学习的一个子领域正在迅速发展，进一步发展和进入既定标准似乎是当前计算和统计硬件进步步伐的一个相当自然和可能的结果。
阅读：贝叶斯网络
贝叶斯机器学习的不同方法
贝叶斯机器学习有三种被广泛接受的方法，即MAP 、MCMC 和“高斯”过程。
使用 MAP的贝叶斯机器学习：最大后验概率
MAP享有作为迈向真正贝叶斯机器学习的第一步的区别。 然而，它在计算像点估计这样基本的东西的能力上是有限的，正如经验丰富的统计学家通常所说的那样。
点估计的问题在于，除了最佳设置之外，它们并没有透露太多关于参数的信息。 分析师和统计学家经常追求额外的、核心有价值的信息，例如，某个参数值落在这个预定义范围内的概率。 毕竟，这就是贝叶斯机器学习的真正预测能力所在。
使用 MCMC 进行贝叶斯机器学习：马尔可夫链蒙特卡罗
马尔可夫链蒙特卡罗，也通常称为 MCMC，是一种流行且著名的“伞形”算法，通过一组著名的辅助方法如 Gibbs 和 Slice Sampling 应用。
虽然 MCMC 的数学通常被认为是困难的，但它仍然同样有趣和令人印象深刻。 这些辅助方法的高潮是构建一个已知的马尔可夫链，进一步确定一个与后验等效的分布。
许多连续的算法选择通过包含梯度信息来改进 MCMC 方法，以试图让分析人员以更高的效率导航参数空间。
然而，有更简单的方法可以实现这种准确性。 例如，有贝叶斯线性和逻辑回归等价物，其中分析师使用拉普拉斯近似。 后验分布的解析近似（可以在纸上解释）是这个过程与众不同的地方。
必读：朴素贝叶斯解释
使用高斯过程的贝叶斯机器学习
高斯过程是一个随机过程，对所有组成随机变量施加严格的高斯条件。 它们的工作原理是确定所有可能行的空间上的概率分布，然后在考虑数据的情况下选择最有可能成为实际预测变量的行。
这些过程最终允许分析师在功能空间中执行回归。 鉴于整个后验分布是在这种方法中进行分析计算的，这无疑是最真实的贝叶斯估计，因此在统计和逻辑上都是最令人钦佩的。
如果您想了解更多关于机器学习和人工智能职业的信息，请查看 IIT Madras 和 upGrad 的机器学习和云高级认证。