Bayesian Machine Learning – สำรวจการเปลี่ยนแปลงกระบวนทัศน์ในการสร้างแบบจำลองข้อมูลทางสถิติ
เผยแพร่แล้ว: 2020-11-24สารบัญ
Bayesian Machine Learning คืออะไร?
Bayesian Machine Learning (หรือที่เรียกว่า Bayesian ML) เป็นวิธีที่เป็นระบบในการสร้างแบบจำลองทางสถิติ โดยอิงตามทฤษฎีบทของ Bayes
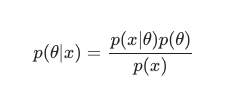 ปัญหาการเรียนรู้ของเครื่องมาตรฐานรวมถึงชุดข้อมูลหลักสองชุดที่ต้องการการวิเคราะห์:
ปัญหาการเรียนรู้ของเครื่องมาตรฐานรวมถึงชุดข้อมูลหลักสองชุดที่ต้องการการวิเคราะห์:
- ชุดข้อมูลการฝึกอบรมที่ครอบคลุม
- ชุดของ อินพุต ที่มีอยู่ทั้งหมดและ เอาต์พุต ที่ บันทึกไว้ทั้งหมด
วิธีดั้งเดิมในการวิเคราะห์ข้อมูลนี้สำหรับการสร้างแบบจำลองคือการกำหนดรูปแบบบางอย่างที่สามารถจับคู่ระหว่างชุดข้อมูลเหล่านี้ได้ นักวิเคราะห์มักจะประกบโมเดลเข้าด้วยกันเพื่อกำหนดการทำแผนที่ระหว่างสิ่งเหล่านี้ และวิธีการที่เป็นผลลัพธ์เป็นวิธีที่กำหนดได้มากในการสร้างการคาดการณ์สำหรับตัวแปรเป้าหมาย
ปัญหาเดียวคือไม่มีทางอธิบายสิ่งที่เกิดขึ้น ภายใน โมเดลนี้อย่างแน่นอนด้วยชุดคำจำกัดความที่ชัดเจน ทั้งหมดที่ทำได้โดยพื้นฐานแล้วคือการลดฟังก์ชันการสูญเสียบางอย่างในชุดข้อมูลการฝึกอบรม - แต่แทบจะไม่มีคุณสมบัติเป็น แบบจำลอง ที่แท้จริง
โมเดลในอุดมคติ (และควรเป็นแบบไม่มีการสูญเสีย) เป็นการสรุปวัตถุประสงค์ของพารามิเตอร์โดยธรรมชาติของแบบจำลอง เสริมด้วยไข่อีสเตอร์ทางสถิติ (เช่น ช่วงความเชื่อมั่น) ที่สามารถกำหนดและป้องกันในภาษาของความน่าจะเป็นทางคณิตศาสตร์ สถานการณ์สมมติ "ในอุดมคติ" นี้คือสิ่งที่ Bayesian Machine Learning กำหนดให้สำเร็จ
เป้าหมาย (และความมหัศจรรย์) ของการเรียนรู้เครื่องจักรแบบเบย์
วัตถุประสงค์หลักของ Bayesian Machine Learning คือการประมาณการ แจกแจง ภายหลัง โดยพิจารณาจากความ น่าจะ เป็น (การประมาณการอนุพันธ์ของข้อมูลการฝึกอบรม) และการ แจกแจง ก่อน หน้า

เมื่อฝึกโมเดลแมชชีนเลิร์นนิงทั่วไป นี่คือสิ่งที่เราทำในทางทฤษฎีและการปฏิบัติ เป็นที่ทราบกันดีว่านักวิเคราะห์ดำเนินการทำซ้ำ การประมาณค่าความน่าจะเป็นสูงสุด ในข้อมูลการฝึกอบรม ดังนั้นจึงอัปเดตพารามิเตอร์ของแบบจำลองในลักษณะที่เพิ่มความน่าจะเป็นสูงสุดในการดู มันนำไปสู่ปัญหาไก่กับไข่ ซึ่ง Bayesian Machine Learning มีเป้าหมายที่จะแก้ไขอย่างสวยงาม
สิ่งต่าง ๆ เปลี่ยนไปอย่างสิ้นเชิงในกรณีที่นักวิเคราะห์พยายาม เพิ่ม การ กระจายหลัง สมมติว่าข้อมูลการฝึกอบรมได้รับการแก้ไข และด้วยเหตุนี้จึงกำหนดความน่าจะเป็นของ การตั้งค่าพารามิเตอร์ ใดๆ ที่มาพร้อมกับข้อมูลดังกล่าว กระบวนการนี้เรียกว่า Maximum A Posteriori ย่อ เป็น MAP วิธีที่ง่ายกว่าในการทำความเข้าใจแนวคิดนี้คือการคิดในแง่ของ ฟังก์ชัน ความ น่าจะ เป็น
เมื่อพิจารณา ทฤษฎีบท ของเบย์ แล้ว สันหลังสามารถนิยามได้ดังนี้:
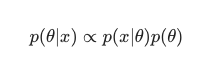
ในสถานการณ์สมมตินี้ เราปล่อยให้ตัวส่วนเป็นมาตรการป้องกันการซ้ำซ้อนอย่างง่าย สิ่งใดก็ตามที่ไม่ก่อให้เกิดการพึ่งพาแบบจำลองสามารถละเว้นได้ในขั้นตอนการขยายใหญ่สุด จิ๊กซอว์ชิ้นสำคัญของจิ๊กซอว์นี้ คือการแจกแจงล่วงหน้า เป็นสิ่งที่ทำให้โมเดลเบย์เซียนโดดเด่นแตกต่างไปจากเกมคลาสสิกที่ได้รับการฝึกอบรมจาก MLE
นักวิเคราะห์มักจะตั้งสมมติฐานที่สมเหตุสมผลว่าการกำหนดค่าพารามิเตอร์เฉพาะมีความเหมาะสมเพียงใด และวิธีนี้เป็นวิธีที่ยาวนานในการเข้ารหัสความเชื่อของพวกเขาเกี่ยวกับพารามิเตอร์เหล่านี้ แม้กระทั่งก่อนที่พวกเขาจะได้เห็นพารามิเตอร์เหล่านั้นแบบเรียลไทม์ เป็นเรื่องธรรมดา ตัวอย่างเช่น ที่จะใช้ Gaussian ก่อนพารามิเตอร์ของแบบจำลอง
นักวิเคราะห์คาดการณ์ว่าพารามิเตอร์เหล่านี้มาจากการแจกแจงแบบปกติ โดยจะแสดงทั้งค่าเฉลี่ยและความแปรปรวน การกระจายประเภทนี้มีรูปทรงโค้งระฆังแบบคลาสสิก รวมส่วนสำคัญของมวลของมัน ใกล้เคียงกับค่าเฉลี่ยอย่างน่าประทับใจ

ในทางกลับกัน ค่าที่เกิดขึ้นที่ส่วนท้ายนั้นค่อนข้างหายาก การใช้คำสั่งก่อนหน้านี้อย่างมีประสิทธิภาพระบุถึงความเชื่อที่ว่า ตุ้มน้ำหนักของ แบบ จำลองส่วนใหญ่ต้องอยู่ภายในช่วงแคบที่กำหนดไว้ ซึ่ง ใกล้เคียงกับค่ากลางมากโดยมีค่าผิดปกติพิเศษเพียงเล็กน้อยเท่านั้น นี่เป็นความเชื่อที่สมเหตุสมผลที่จะไล่ตาม โดยคำนึงถึงปรากฏการณ์ในโลกแห่งความเป็นจริงและสถานการณ์ที่ไม่เหมาะในการพิจารณา
อย่างไรก็ตาม ผลกระทบของแบบจำลองเบย์นั้นน่าสนใจยิ่งขึ้นไปอีกเมื่อคุณสังเกตว่าการใช้การแจกแจงก่อนหน้าเหล่านี้ (และ กระบวนการ MAP ) สร้างผลลัพธ์ที่ใกล้เคียงกันอย่างมาก หากไม่เท่ากับการแก้ไขโดยการดำเนินการ MLE ในความหมายดั้งเดิม ช่วยในการปรับให้สม่ำเสมอ
เป็นเรื่องน่าขบขันมากที่สังเกตว่าเพียงแค่จำกัดน้ำหนักของโมเดลที่ "ยอมรับ" กับน้ำหนักก่อนหน้า เราก็สร้างตัวปรับน้ำหนักได้
โดยรวมแล้ว Bayesian Machine Learning มีการพัฒนาอย่างรวดเร็วในฐานะสาขาย่อยของการเรียนรู้ด้วยเครื่อง และการพัฒนาเพิ่มเติมและการรุกเข้าสู่ Canon ที่เป็นที่ยอมรับดูเหมือนจะเป็นผลที่เป็นธรรมชาติและน่าจะเป็นไปได้ของความก้าวหน้าในฮาร์ดแวร์คอมพิวเตอร์และสถิติในปัจจุบัน
อ่าน: Bayesian Networks
วิธีการต่างๆ ของการเรียนรู้ด้วยเครื่อง Bayesian
Bayesian Machine Learning มีสามวิธีที่เป็นที่ยอมรับกันมาก ได้แก่ MAP , MCMC และกระบวนการ "Gaussian"
Bayesian Machine Learning พร้อม MAP: สูงสุด A Posteriori
MAP สนุกกับความแตกต่างของการเป็นก้าวแรกสู่การเรียนรู้เครื่อง Bayesian อย่างแท้จริง อย่างไรก็ตาม ความสามารถในการคำนวณบางอย่างเป็นเพียงการประมาณการแบบจุดเท่านั้น ซึ่งมักเรียกกันว่านักสถิติที่มีประสบการณ์
ปัญหาของการประมาณแบบจุดคือพวกเขาไม่ได้เปิดเผยอะไรมากเกี่ยวกับพารามิเตอร์อื่นนอกเหนือจากการตั้งค่าที่เหมาะสมที่สุด นักวิเคราะห์และนักสถิติมักจะแสวงหาข้อมูลเพิ่มเติมที่มีคุณค่าหลัก เช่น ความน่าจะ เป็นที่ค่าพารามิเตอร์บางตัวจะตกอยู่ในช่วงที่กำหนดไว้ล่วงหน้านี้ เพราะนั่นคือจุดที่พลังการทำนายที่แท้จริงของ Bayesian Machine Learning อยู่
Bayesian Machine Learning กับ MCMC: Markov Chain Monte Carlo
Markov Chain Monte Carlo หรือที่รู้จักกันทั่วไปในชื่อ MCMC เป็นอัลกอริธึม "ร่ม" ที่ได้รับความนิยมและโด่งดัง โดยนำไปใช้ผ่านชุดวิธีการย่อยที่มีชื่อเสียง เช่น Gibbs และ Slice Sampling
และในขณะที่คณิตศาสตร์ของ MCMC โดยทั่วไปถือว่ายาก แต่ก็ยังมีความน่าสนใจและน่าประทับใจไม่แพ้กัน จุดสุดยอดของวิธีการย่อยเหล่านี้คือการสร้างห่วงโซ่ Markov ที่เป็นที่รู้จัก ตกตะกอนเพิ่มเติมในการกระจายที่เทียบเท่ากับส่วนหลัง
อัลกอริธึมที่ต่อเนื่องกันจำนวนมากได้เลือกที่จะปรับปรุงวิธีการ MCMC โดยการรวมข้อมูลการไล่ระดับสีในความพยายามที่จะให้นักวิเคราะห์สำรวจพื้นที่พารามิเตอร์ด้วยประสิทธิภาพที่เพิ่มขึ้น

มีวิธีที่ง่ายกว่าในการบรรลุความแม่นยำนี้อย่างไรก็ตาม ตัวอย่างเช่น มีการเทียบเท่าการถดถอยเชิงเส้นและการถดถอยโลจิสติกแบบเบย์ ซึ่งนักวิเคราะห์ใช้การ ประมาณลาปลา ซ การประมาณเชิงวิเคราะห์ (ที่สามารถอธิบายได้บนกระดาษ) ต่อการแจกแจงภายหลังคือสิ่งที่ทำให้กระบวนการนี้แตกต่างออกไป
ต้องอ่าน: Naive Bayes อธิบาย
Bayesian Machine Learning ด้วยกระบวนการเกาส์เซียน
กระบวนการ เกาส์เซียน เป็นกระบวนการสุ่ม โดยมีการกำหนดเงื่อนไขเกาส์เซียนที่เข้มงวดกับองค์ประกอบทั้งหมด ตัวแปรสุ่ม พวกมันทำงานโดยกำหนดการกระจายความน่าจะเป็นบนช่องว่างของเส้นที่เป็นไปได้ทั้งหมด แล้วเลือกเส้นที่มีแนวโน้มว่าจะเป็นตัวทำนายจริงมากที่สุด โดยนำข้อมูลมาพิจารณาด้วย
กระบวนการเหล่านี้ทำให้นักวิเคราะห์สามารถถดถอยในพื้นที่ฟังก์ชันได้ เนื่องจากการ แจกแจงภายหลังทั้งหมด ถูกคำนวณในเชิงวิเคราะห์ในวิธีนี้ ไม่ต้องสงสัยเลยว่าการประมาณค่าแบบเบย์นั้นเป็นจริงที่สุดอย่างไม่ต้องสงสัย และด้วยเหตุนี้ทั้งทางสถิติและเชิงตรรกะจึงเป็นสิ่งที่น่าชื่นชมมากที่สุด
หากคุณต้องการทราบข้อมูลเพิ่มเติมเกี่ยวกับอาชีพในแมชชีนเลิร์นนิงและปัญญาประดิษฐ์ โปรดดูที่ IIT Madras และการรับรองขั้นสูงของ upGrad ในการเรียนรู้ของเครื่องและคลาวด์
