Байесовское машинное обучение — исследование смены парадигмы в статистическом моделировании данных
Опубликовано: 2020-11-24Оглавление
Что такое байесовское машинное обучение?
Байесовское машинное обучение (также известное как байесовское машинное обучение) — это систематический подход к построению статистических моделей, основанный на теореме Байеса.
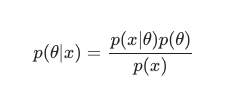Любая стандартная задача машинного обучения включает в себя два основных набора данных, требующих анализа:
- Полный набор обучающих данных
- Коллекция всех доступных входов и всех записанных выходов
Традиционный подход к анализу этих данных для моделирования заключается в определении некоторых закономерностей, которые можно сопоставить между этими наборами данных. Аналитик обычно объединяет модель, чтобы определить соответствие между ними, и полученный в результате подход является очень детерминированным методом для создания прогнозов для целевой переменной.
Единственная проблема заключается в том, что совершенно невозможно объяснить, что происходит внутри этой модели, с помощью четкого набора определений. По сути, все, что достигается, — это минимизация некоторых функций потерь в обучающем наборе данных, но вряд ли это можно назвать настоящим моделированием.
Идеальная (и желательно без потерь) модель предполагает объективную сводку присущих модели параметров, дополненную статистическими пасхальными яйцами (такими как доверительные интервалы), которые можно определить и защитить на языке математической вероятности. Этот «идеальный» сценарий — это то, к чему стремится байесовское машинное обучение.
Цели (и магия) байесовского машинного обучения
Основная цель байесовского машинного обучения — оценить апостериорное распределение с учетом вероятности (производной оценки обучающих данных) и априорного распределения .
При обучении обычной модели машинного обучения именно этим мы и занимаемся в теории и на практике. Известно, что аналитики выполняют последовательные итерации оценки максимального правдоподобия для обучающих данных, тем самым обновляя параметры модели таким образом, чтобы максимизировать вероятность увидеть Это приводит к проблеме курицы и яйца, которую байесовское машинное обучение стремится красиво решить.
Все принимает совершенно другой оборот в данном случае, когда аналитик стремится максимизировать апостериорное распределение , предполагая, что обучающие данные фиксированы, и тем самым определяя вероятность любого параметра, который сопровождает указанные данные. Этот процесс называется Максимум Апостериори , сокращенно MAP . Более простой способ понять эту концепцию — подумать о ней с точки зрения функции правдоподобия .
Принимая во внимание теорему Байеса , апостериор можно определить как:
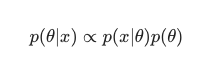
В этом сценарии мы опускаем знаменатель как простую меру против избыточности. Все, что не вызывает зависимости от модели, может быть проигнорировано в процедуре максимизации. Эта ключевая часть головоломки, предварительное распределение, позволяет байесовским моделям выделяться на фоне их классических аналогов, обученных MLE.
Аналитики часто могут делать разумные предположения о том, насколько хорошо подходит конкретная конфигурация параметров, и это имеет большое значение для кодирования их убеждений об этих параметрах еще до того, как они увидят их в реальном времени. Например, относительно обычным является использование гауссовского априорного значения параметров модели.
Аналитик здесь предполагает, что эти параметры были взяты из нормального распределения с некоторым отображением как среднего, так и дисперсии. Этот вид распределения имеет классическую колоколообразную форму, объединяющую значительную часть его массы, впечатляюще близкую к среднему значению.
С другой стороны, вхождения значений ближе к концу довольно редки. Использование такого априорного значения фактически утверждает убеждение, что большинство весов модели должны соответствовать определенному узкому диапазону , очень близкому к среднему значению с несколькими исключительными выбросами. Это разумное убеждение, которому следует следовать, принимая во внимание явления реального мира и неидеальные обстоятельства.
Эффекты байесовской модели, однако, еще более интересны, когда вы замечаете, что использование этих априорных распределений (и процесса MAP ) дает результаты, которые поразительно похожи, если не равны тем, которые получены при выполнении MLE в классическом смысле. помог с некоторой дополнительной регуляризацией.
Очень забавно отметить, что просто ограничивая «принятые» веса модели априорным значением, мы в конечном итоге создаем регуляризатор.
В целом байесовское машинное обучение быстро развивается как подобласть машинного обучения, и дальнейшее развитие и проникновение в установленный канон кажутся довольно естественным и вероятным результатом нынешних темпов развития вычислительного и статистического оборудования.
Читайте: Байесовские сети
Различные методы байесовского машинного обучения
Существует три общепринятых подхода к байесовскому машинному обучению, а именно MAP , MCMC и «гауссовский» процесс.
Байесовское машинное обучение с MAP: максимум апостериорно
MAP отличается тем, что является первым шагом к истинному байесовскому машинному обучению. Однако он ограничен в своих возможностях вычислять что-то столь элементарное, как точечная оценка, как это обычно называют опытные статистики.
Проблема с точечными оценками заключается в том, что они мало что говорят о параметре, кроме его оптимальной настройки. Аналитики и статистики часто ищут дополнительную, основную ценную информацию, например, вероятность того, что значение определенного параметра попадет в этот заранее определенный диапазон. В конце концов, именно в этом заключается настоящая предсказательная сила байесовского машинного обучения.
Байесовское машинное обучение с MCMC: цепь Маркова Монте-Карло
Цепь Маркова Монте-Карло, также известная как MCMC, является популярным и знаменитым «зонтичным» алгоритмом, применяемым с помощью набора известных вспомогательных методов, таких как Gibbs и Slice Sampling.
И хотя математика MCMC обычно считается сложной, она остается столь же интригующей и впечатляющей. Кульминацией этих вспомогательных методов является построение известной цепи Маркова, в дальнейшем приводящее к распределению, эквивалентному апостериорному.
Многие последовательные алгоритмы решили улучшить метод MCMC, включив информацию о градиенте, чтобы позволить аналитикам перемещаться в пространстве параметров с большей эффективностью.
Однако есть более простые способы добиться такой точности. Например, существуют эквиваленты байесовской линейной и логистической регрессии, в которых аналитики используют приближение Лапласа . Аналитическое приближение (которое можно объяснить на бумаге) к апостериорному распределению — вот что отличает этот процесс.
Должен прочитать: объяснение наивного Байеса
Байесовское машинное обучение с гауссовским процессом
Гауссовский процесс — это стохастический процесс, в котором на все составляющие случайные величины накладываются строгие гауссовские условия . Они работают, определяя распределение вероятностей в пространстве всех возможных линий, а затем выбирая линию, которая, скорее всего, будет фактическим предиктором, принимая во внимание данные.
Эти процессы в конечном итоге позволяют аналитикам выполнять регрессию в функциональном пространстве. Учитывая, что в этом методе аналитически вычисляется все апостериорное распределение , это, несомненно, байесовская оценка в ее самом истинном виде и, следовательно, как статистически, так и логически наиболее замечательная.
Если вы хотите узнать больше о карьере в области машинного обучения и искусственного интеллекта, ознакомьтесь с IIT Madras и расширенной сертификацией upGrad в области машинного обучения и облачных вычислений.