التعلم الآلي البايزي - استكشاف تحول نموذجي في نمذجة البيانات الإحصائية
نشرت: 2020-11-24جدول المحتويات
ما هو التعلم الآلي بايزي؟
Bayesian Machine Learning (المعروف أيضًا باسم Bayesian ML) هو نهج منظم لبناء نماذج إحصائية ، بناءً على نظرية بايز.
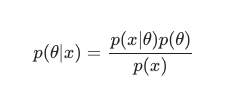تتضمن أي مشكلة قياسية في التعلم الآلي مجموعتي بيانات أساسيتين تحتاجان إلى التحليل:
- مجموعة شاملة من بيانات التدريب
- مجموعة من جميع المدخلات المتاحة وجميع المخرجات المسجلة
تتمثل الطريقة التقليدية لتحليل هذه البيانات من أجل النمذجة في تحديد بعض الأنماط التي يمكن تعيينها بين مجموعات البيانات هذه. عادةً ما يقوم المحلل بربط نموذج معًا لتحديد التعيين بينهما ، والنهج الناتج هو طريقة حتمية للغاية لإنشاء تنبؤات لمتغير مستهدف.
المشكلة الوحيدة هي أنه لا توجد طريقة على الإطلاق لشرح ما يحدث داخل هذا النموذج بمجموعة واضحة من التعريفات. كل ما يتم إنجازه ، بشكل أساسي ، هو تقليل بعض وظائف الخسارة في مجموعة بيانات التدريب - لكن هذا بالكاد يمكن اعتباره نموذجًا حقيقيًا .
يستلزم النموذج المثالي (ويفضل أن يكون بلا خسارة) ملخصًا موضوعيًا للمعلمات المتأصلة في النموذج ، مع استكمالها ببيض عيد الفصح الإحصائي (مثل فترات الثقة) التي يمكن تعريفها والدفاع عنها بلغة الاحتمال الرياضي. هذا السيناريو "المثالي" هو ما تسعى Bayesian Machine Learning إلى تحقيقه.
أهداف (وسحر) التعلم الآلي البايزي
الهدف الأساسي من Bayesian Machine Learning هو تقدير التوزيع اللاحق ، بالنظر إلى الاحتمالية (تقدير مشتق لبيانات التدريب) والتوزيع المسبق .
عند تدريب نموذج تعلم آلي منتظم ، فإن هذا هو بالضبط ما نقوم به في النهاية من الناحية النظرية والتطبيقية. من المعروف أن المحللون يقومون بإجراء تكرارات متتالية لتقدير الاحتمالية القصوى على بيانات التدريب ، وبالتالي تحديث معلمات النموذج بطريقة تزيد من احتمالية رؤية إنه يؤدي إلى مشكلة الدجاج والبيض ، والتي تهدف Bayesian Machine Learning إلى حلها بشكل جميل.
تأخذ الأمور منعطفًا مختلفًا تمامًا في حالة معينة حيث يسعى المحلل إلى زيادة التوزيع اللاحق إلى أقصى حد ، بافتراض أن بيانات التدريب ثابتة ، وبالتالي تحديد احتمال أي إعداد معلمة يصاحب البيانات المذكورة. تسمى هذه العملية Maximum A لاحقة ، وتختصر باسم MAP . أسهل طريقة لفهم هذا المفهوم هي التفكير فيه من حيث وظيفة الاحتمال .
مع الأخذ في الاعتبار نظرية بايز ، يمكن تعريف اللاحقة على النحو التالي:
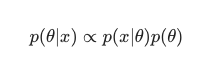
في هذا السيناريو ، نترك المقام خارجًا كإجراء بسيط لمكافحة التكرار. يمكن تجاهل أي شيء لا يسبب الاعتماد على النموذج في إجراء التكبير. هذا الجزء الأساسي من اللغز ، التوزيع المسبق ، هو ما يسمح لنماذج Bayesian بالتميز على عكس نظرائهم الكلاسيكيين المدربين على MLE.
يمكن للمحللين في كثير من الأحيان وضع افتراضات معقولة حول مدى ملاءمة تكوين معلمة معين ، وهذا يقطع شوطًا طويلاً في ترميز معتقداتهم حول هذه المعلمات حتى قبل أن يروها في الوقت الفعلي. من الشائع نسبيًا ، على سبيل المثال ، استخدام علامة غوسية مسبقة على معلمات النموذج.
يفترض المحلل هنا أن هذه المعلمات مأخوذة من توزيع عادي ، مع عرض بعض من المتوسط والتباين. يتميز هذا النوع من التوزيع بشكل منحنى الجرس الكلاسيكي ، مما يعزز جزءًا كبيرًا من كتلته ، وهو قريب بشكل مثير للإعجاب من المتوسط.
من ناحية أخرى ، فإن تكرارات القيم باتجاه الطرف الخلفي نادرة جدًا. يشير استخدام مثل هذه القيمة السابقة بشكل فعال إلى الاعتقاد بأن غالبية أوزان النموذج يجب أن تتناسب مع نطاق ضيق محدد ، قريب جدًا من القيمة المتوسطة مع عدد قليل من القيم المتطرفة الاستثنائية. هذا اعتقاد معقول يجب متابعته ، مع مراعاة ظواهر العالم الحقيقي والظروف غير المثالية.
ومع ذلك ، فإن تأثيرات نموذج Bayesian أكثر إثارة للاهتمام عندما تلاحظ أن استخدام هذه التوزيعات السابقة ( وعملية MAP ) يولد نتائج متشابهة بشكل مذهل ، إن لم تكن مساوية لتلك التي تم حلها عن طريق أداء MLE بالمعنى الكلاسيكي ، بمساعدة بعض التنظيم الإضافي.
إنه لمن الممتع للغاية ملاحظة أنه بمجرد تقييد أوزان النموذج "المقبول" مع السابقة ، ينتهي بنا الأمر إلى إنشاء منظم.
على العموم ، يتطور التعلم الآلي البايزي بسرعة باعتباره مجالًا فرعيًا للتعلم الآلي ، ويبدو أن المزيد من التطوير والتقدم إلى القانون الراسخ هو نتيجة طبيعية إلى حد ما ومن المحتمل أن تكون نتيجة التقدم الحالي في الأجهزة الحسابية والإحصائية.
قراءة: شبكات بايزي
الطرق المختلفة لتعلم آلة بايزي
هناك ثلاثة مناهج مقبولة إلى حد كبير لتعلم الآلة Bayesian ، وهي MAP و MCMC وعملية "Gaussian".
التعلم الآلي باستخدام MAP بايزي: الحد الأقصى من اللاحق
تتمتع MAP بكونها الخطوة الأولى نحو التعلم الآلي الحقيقي Bayesian. ومع ذلك ، فهي محدودة في قدرتها على حساب شيء بدائي مثل تقدير النقاط ، كما يشار إليه عادة من قبل الإحصائيين ذوي الخبرة.
تكمن مشكلة تقديرات النقاط في أنها لا تكشف الكثير عن معلمة بخلاف الإعداد الأمثل لها. غالبًا ما يسعى المحللون والإحصائيون إلى الحصول على معلومات قيمة إضافية جوهرية ، على سبيل المثال ، احتمال وقوع قيمة معلمة معينة ضمن هذا النطاق المحدد مسبقًا. بعد كل شيء ، هذا هو المكان الذي تكمن فيه القوة التنبؤية الحقيقية لتعلم الآلة البايزية.
تعلم الآلة بايزي مع MCMC: ماركوف تشين مونت كارلو
Markov Chain Monte Carlo ، المعروف أيضًا باسم MCMC ، هو خوارزمية "مظلة" مشهورة ومشهورة ، يتم تطبيقها من خلال مجموعة من الأساليب الفرعية الشهيرة مثل Gibbs و Slice Sampling.
وعلى الرغم من أن رياضيات MCMC تعتبر صعبة بشكل عام ، إلا أنها لا تزال مثيرة للاهتمام ومثيرة للإعجاب. تتويج هذه الأساليب الفرعية ، وهي بناء سلسلة ماركوف المعروفة ، واستقرارها بشكل أكبر في التوزيع الذي يعادل السلسلة اللاحقة.
اختارت العديد من الخوارزميات المتتالية تحسين طريقة MCMC من خلال تضمين معلومات التدرج في محاولة للسماح للمحللين بالتنقل في مساحة المعلمة بكفاءة متزايدة.
ومع ذلك ، هناك طرق أبسط لتحقيق هذه الدقة. على سبيل المثال ، هناك معادلات الانحدار الخطي واللوجستي Bayesian ، حيث يستخدم المحللون تقريب لابلاس . التقريب التحليلي (الذي يمكن شرحه على الورق) للتوزيع اللاحق هو ما يميز هذه العملية عن بعضها.
يجب أن تقرأ: شرح بايز ساذج
Bayesian Machine Learning مع عملية Gaussian
عملية Gaussian هي عملية عشوائية ، مع فرض شروط Gaussian الصارمة على جميع المتغيرات المكونة والعشوائية. إنهم يعملون عن طريق تحديد توزيع احتمالي على مساحة جميع الخطوط المحتملة ثم اختيار الخط الذي من المرجح أن يكون المتنبئ الفعلي ، مع مراعاة البيانات.
تنتهي هذه العمليات بالسماح للمحللين بأداء الانحدار في مساحة الوظيفة. بالنظر إلى أن التوزيع اللاحق بأكمله يتم حسابه بشكل تحليلي بهذه الطريقة ، فإن هذا بلا شك تقدير بايزي في صدقه ، وبالتالي فهو الأكثر إثارة للإعجاب من الناحيتين الإحصائية والمنطقية.
إذا كنت ترغب في معرفة المزيد عن الوظائف في التعلم الآلي والذكاء الاصطناعي ، تحقق من IIT Madras وشهادة upGrad المتقدمة في التعلم الآلي والسحابة.