Bayesian Machine Learning – İstatistiksel Veri Modellemede Bir Paradigma Değişimini Keşfetmek
Yayınlanan: 2020-11-24İçindekiler
Bayesian Makine Öğrenimi Nedir?
Bayesian Machine Learning (Bayesian ML olarak da bilinir), Bayes Teoremine dayalı istatistiksel modeller oluşturmaya yönelik sistematik bir yaklaşımdır.
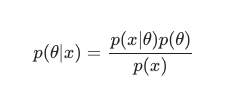Herhangi bir standart makine öğrenimi sorunu, analiz edilmesi gereken iki birincil veri kümesini içerir:
- Kapsamlı bir eğitim verisi seti
- Mevcut tüm girdilerin ve tüm kayıtlı çıktıların bir koleksiyonu
Bu verileri modelleme için analiz etmeye yönelik geleneksel yaklaşım, bu veri kümeleri arasında eşlenebilecek bazı kalıpları belirlemektir. Bir analist, bunlar arasındaki eşlemeyi belirlemek için genellikle bir modeli birbirine ekler ve sonuçta ortaya çıkan yaklaşım, bir hedef değişken için tahminler oluşturmak için çok belirleyici bir yöntemdir.
Tek sorun, bu modelin içinde neler olup bittiğini net tanımlarla açıklamanın kesinlikle bir yolu olmamasıdır . Gerçekleştirilen tek şey, temel olarak, eğitim veri setindeki bazı kayıp fonksiyonlarının en aza indirilmesidir - ancak bu, gerçek modelleme olarak pek nitelendirilemez.
İdeal (ve tercihen kayıpsız) bir model, matematiksel olasılık dilinde tanımlanabilen ve savunulabilen istatistiksel paskalya yumurtaları (güven aralıkları gibi) ile desteklenen modelin doğal parametrelerinin nesnel bir özetini gerektirir. Bu "ideal" senaryo, Bayesian Machine Learning'in başarmak için yola çıktığı şeydir.
Bayesian Machine Learning'in Hedefleri (Ve Büyüsü)
Bayesian Machine Learning'in birincil amacı , olabilirlik (eğitim verilerinin türev tahmini) ve önceki dağılım göz önüne alındığında sonsal dağılımı tahmin etmektir .
Normal bir makine öğrenimi modelini eğitirken, teoride ve pratikte yaptığımız tam olarak budur. Analistlerin eğitim verileri üzerinde art arda Maksimum Olabilirlik Tahmini yinelemelerini gerçekleştirdikleri ve böylece modelin parametrelerini Bayesian Machine Learning'in güzelce çözmeyi amaçladığı bir tavuk-yumurta sorununa yol açar.
Bir analistin eğitim verilerinin sabitleneceğini varsayarak ve böylece söz konusu verilere eşlik eden herhangi bir parametre ayarının olasılığını belirleyerek sonsal dağılımı Bu işleme Maximum A Posteriori denir ve MAP olarak kısaltılır . Bu kavramı kavramanın daha kolay bir yolu, onun hakkında olabilirlik fonksiyonu açısından düşünmektir .
Bayes Teoremi dikkate alınarak, posterior şu şekilde tanımlanabilir:
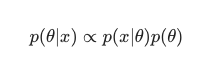
Bu senaryoda, paydayı basit bir fazlalık önleme önlemi olarak dışarıda bırakıyoruz. Modele bağımlılığa neden olmayan herhangi bir şey maksimizasyon prosedüründe göz ardı edilebilir. Bulmacanın bu önemli parçası, önceki dağıtım, Bayes modellerinin klasik MLE eğitimli muadillerinin aksine öne çıkmasını sağlayan şeydir.
Analistler, belirli bir parametre konfigürasyonunun ne kadar uygun olduğu konusunda genellikle makul varsayımlarda bulunabilirler ve bu, bu parametreler hakkındaki inançlarını gerçek zamanlı olarak görmeden önce bile kodlamada uzun bir yol kat eder. Örneğin, modelin parametrelerinden önce bir Gauss kullanmak nispeten yaygındır.
Buradaki analist, bu parametrelerin hem ortalama hem de varyansın bir miktar gösterimi ile normal bir dağılımdan alındığını varsayıyor. Bu tür bir dağılım, ortalamaya etkileyici bir şekilde yakın olan kütlesinin önemli bir bölümünü konsolide eden klasik bir çan eğrisi şekline sahiptir.
Öte yandan, kuyruk ucuna doğru değerlerin oluşumu oldukça nadirdir. Böyle bir öncül kullanımı , modelin ağırlıklarının çoğunluğunun, yalnızca birkaç istisnai aykırı değerle ortalama değere çok yakın , tanımlanmış bir dar aralığa uyması gerektiği inancını etkin bir şekilde ifade eder . Bu, gerçek dünyadaki fenomenleri ve ideal olmayan koşulları dikkate alarak, takip edilmesi gereken makul bir inançtır.
Bununla birlikte, bir Bayes modelinin etkileri, bu önceki dağılımların (ve MAP sürecinin) kullanımının, klasik anlamda MLE gerçekleştirerek çözülenlere eşit olmasa bile şaşırtıcı derecede benzer sonuçlar ürettiğini gözlemlediğinizde daha da ilginçtir. bazı ek düzenleme ile yardımcı oldu.
Yalnızca “kabul edilen” model ağırlıklarını öncekiyle sınırlayarak, sonunda bir düzenleyici oluşturduğumuzu belirtmek çok eğlenceli.
Genel olarak, Bayesian Makine Öğrenimi, makine öğreniminin bir alt alanı olarak hızla gelişmektedir ve yerleşik kanonun daha fazla geliştirilmesi ve ilerlemesi, hesaplama ve istatistiksel donanımdaki mevcut ilerleme hızının oldukça doğal ve olası bir sonucu gibi görünmektedir.
Okuyun: Bayes Ağları
Bayesian Machine Learning'in Farklı Yöntemleri
Bayesian Machine Learning için MAP , MCMC ve "Gauss" süreci olmak üzere büyük ölçüde kabul gören üç yaklaşım vardır .
MAP ile Bayesian Machine Learning: Maximum A Posteriori
MAP , gerçek Bayesian Machine Learning yolunda ilk adım olma ayrıcalığına sahiptir. Bununla birlikte, deneyimli istatistikçiler tarafından yaygın olarak ifade edildiği gibi, nokta tahmini olarak ilkel bir şeyi hesaplama yeteneği sınırlıdır.
Nokta tahminleriyle ilgili sorun, bir parametre hakkında optimum ayarı dışında pek bir şey açıklamamalarıdır. Analistler ve istatistikçiler genellikle, örneğin belirli bir parametrenin değerinin bu önceden tanımlanmış aralığa düşme olasılığı gibi ek, temel değerli bilgilerin peşindedir. Ne de olsa Bayesian Machine Learning'in gerçek tahmin gücünün yattığı yer burasıdır.
MCMC ile Bayesian Makine Öğrenimi: Markov Zinciri Monte Carlo
Yaygın olarak MCMC olarak da bilinen Markov Zinciri Monte Carlo, Gibbs ve Slice Sampling gibi bir dizi ünlü yardımcı yöntemle uygulanan popüler ve ünlü bir "şemsiye" algoritmasıdır.
Ve MCMC'nin matematiği genellikle zor kabul edilirken, aynı derecede ilgi çekici ve etkileyici olmaya devam ediyor. Bu yardımcı yöntemlerin doruk noktası, bilinen bir Markov zincirinin inşa edilmesidir ve daha sonra arkaya eşdeğer bir dağılıma yerleşir.
Birbirini izleyen birçok algoritma, analistlerin parametre uzayında artan verimlilikle gezinmesine izin vermek amacıyla gradyan bilgilerini dahil ederek MCMC yöntemini geliştirmeyi seçti.
Bununla birlikte, bu doğruluğu elde etmenin daha basit yolları vardır. Örneğin, analistlerin Laplace Yaklaşımını kullandığı Bayes doğrusal ve lojistik regresyon eşdeğerleri vardır . Sonsal dağılıma analitik bir yaklaşım (kağıt üzerinde açıklanabilir), bu süreci farklı kılan şeydir.
Okumalısınız: Naive Bayes Açıklaması
Gauss süreci ile Bayesian Machine Learning
Gauss süreci , tüm kurucu, rastgele değişkenlere katı Gauss koşullarının uygulandığı stokastik bir süreçtir. Tüm olası çizgilerin alanı üzerinde bir olasılık dağılımı belirleyerek ve ardından verileri hesaba katarak gerçek tahminci olması en muhtemel olan çizgiyi seçerek çalışırlar.
Bu süreçler, analistlerin fonksiyon uzayında regresyon gerçekleştirmesine izin verir. Tüm sonsal dağılımın bu yöntemde analitik olarak hesaplandığı göz önüne alındığında , bu şüphesiz en doğru Bayes tahminidir ve bu nedenle hem istatistiksel hem de mantıksal olarak en takdire şayandır.
Makine Öğrenimi ve Yapay Zeka alanındaki kariyerler hakkında daha fazla bilgi edinmek istiyorsanız, IIT Madras ve upGrad'ın Makine Öğrenimi ve Bulutta Gelişmiş Sertifikasyonuna göz atın.